This is the second entry of a series on Reinforcement Learning, where we explore and develop the ideas behind learning on an interactive scenario. On the previous article we presented what is Reinforcement Learning, how it differentiates from other learning frameworks and why it is worth looking at. On this article, we’ll explore one of the most basic scenarios, from which we can start building the theory behind how Reinforcement Learning agents act and learn from the environment.
这是“强化学习”系列的第二篇文章,我们将在交互式场景中探索和发展背后的思想。 在上一篇文章中,我们介绍了什么是强化学习,它与其他学习框架的区别以及为什么值得研究。 在本文上,我们将探讨一种最基本的方案,从中我们可以开始构建强化学习代理如何行动并从环境中学习的理论。
On this article, we’ll cover both theory and code. Some of the code snippets will be presented here, but I strongly recommend following along with this notebook I’ve prepared for this article.
在本文中,我们将介绍理论和代码。 一些代码片段将在此处显示,但是我强烈建议您跟随本文准备的笔记本一起阅读。
多武装强盗场景 (The multi-Armed Bandit Scenario)
We find ourselves in a casino, hoping that both strategy and luck will yield us a great amount of profit. In this casino there’s a known number of armed bandits from which we can try our luck. All bandits behave randomly, but on average, each of them will return a specified profit. Some bandits have higher returns, and therefore there’s necessarily one bandit that will give a return higher or equal to any other bandit. How do you go finding such armed-bandit? Given that we want to maximize our profit (and therefore also minimize our loss) what would be the best strategy?
我们发现自己在赌场中,希望策略和运气都能为我们带来大量利润。 在这家赌场中,有一定数量的武装匪徒,我们可以试试运气。 所有土匪行为随机,但平均而言,每个土匪会返回指定的利润。 有些土匪的收益较高,因此一定有一个土匪的收益高于或等于任何其他土匪。 您如何找到这种武装匪徒? 假设我们要最大化利润(因此也将损失最小化),那么最佳策略是什么?

Let’s start by creating such scenario. We’re going to use OpenAI’s gym to build an environment that behaves like the casino explained above.
让我们从创建这样的场景开始。 我们将使用OpenAI的健身房来构建一个行为类似于上述赌场的环境。
from gym import spaces
from gym.utils import seeding
import numpy as np
class ArmedBanditsEnv(gym.Env):
"""
The famous k-Armed Bandit Environment, implemented for the gym interface.
Initialization requires an array for the mean of each bandit,
as well as another array for the deviation from the mean for
each bandit. This arrays are then used to sample from the
distribution of a given bandit.
"""
metadata = {'render.modes': ['human']}
def __init__(self, mean, stddev):
assert len(mean.shape) == 2
assert len(stddev.shape) == 2
super(ArmedBanditsEnv, self).__init__()
# Define action and observation space
self.num_bandits = mean.shape[1]
self.num_experiments = mean.shape[0]
self.action_space = spaces.Discrete(self.num_bandits)
# Theres one state only in the k-armed bandits problem
self.observation_space = spaces.Discrete(1)
self.mean = mean
self.stddev = stddev
def step(self, action):
# Sample from the specified bandit using it's reward distribution
assert (action < self.num_bandits).all()
sampled_means = self.mean[np.arange(self.num_experiments),action]
sampled_stddevs = self.stddev[np.arange(self.num_experiments),action]
reward = np.random.normal(loc=sampled_means, scale=sampled_stddevs, size=(self.num_experiments,))
# Return a constant state of 0. Our environment has no terminal state
observation, done, info = 0, False, dict()
return observation, reward, done, infoFrom the above implementation, we can create an environment where we define both the number of bandits our casino has, as well as their mean profit and deviation from the mean. Whenever we interact with the environment, we have to specify which bandit we choose to pull, and the environment returns a reward for that action. Here’s a small example:
通过上述实现,我们可以创建一个环境,在该环境中定义赌场拥有的土匪数量以及其平均利润和均值偏差。 每当我们与环境互动时,我们都必须指定我们选择拉哪个土匪,而环境会为该行为带来回报。 这是一个小例子:
means = np.array([[5, 1, 0, -10]]) # The mean for four armed bandits
stdev = np.array([[1, 0.1, 5, 1]]) # The standard deviation for four armed bandits
env = ArmedBanditsEnv(means, stdev) # Create the environment
for i in range(4):
action = np.array([[i]])
_, reward, _, _ = env.step(action)
print("Bandit:", i, " gave a reward of:", reward[0])
From the above example, we created four bandits, where the first one has the highest mean profit of 5, while the last one has the lowest mean profit of -10. We interacted with each of the bandits to see what reward it gave us. The rewards are random, but they fall near the mean of each bandit. The deviation determines how far away those random rewards will be for each bandit. Notice that the second bandit (Bandit 1) has a really low deviation, and so the random values fall very close to the mean. The third bandit (Bandit 2) has a higher standard deviation, which means we can find values very far apart from the average.
从上面的示例中,我们创建了四个土匪,其中第一个土匪的平均利润最高,为5,而最后一个土匪的平均利润最低,为-10。 我们与每个土匪进行了互动,以了解它给了我们什么奖励。 奖励是随机的,但它们接近每个匪徒的平均值。 偏差决定了每个匪徒的随机奖励将走多远。 请注意,第二个土匪(土匪1)的偏差非常小,因此随机值非常接近均值。 第三个强盗(强盗2)具有较高的标准偏差,这意味着我们可以找到与平均值相差很远的值。
The effect of randomness is crucial in this scenario. Sometimes we’re lucky, and get a very high value for a bandit, but sometimes we aren’t that lucky. Interacting with each bandit once doesn’t tell us how good that bandit is overall. Sometimes, a bandit with low average but high variance could give us a lucky jackpot, but other bandits could return us an overall better result.
在这种情况下,随机性的影响至关重要。 有时我们很幸运,并且为匪徒获得了很高的价值,但有时我们并不那么幸运。 与每个土匪进行一次互动并不能告诉我们该土匪的整体状况如何。 有时,平均水平低但方差高的土匪可以给我们带来幸运的头奖,但是其他土匪可以为我们带来总体更好的结果。
This is an extremely familiar situation. Even if you’re not into gambling, you find yourself having to take these kind of decisions all the time. Whenever you’re at a restaurant, you have to decide what dish you want. Should you go for that dish you’ve already tried and know you like? Or will you take a shot with another dish? There’s a chance you could find a new favorite dish, or end up regretting not going for the safer choice. This is known as the Exploration-Exploitation Dilemma.
这是一个非常熟悉的情况。 即使您不赌博,也会发现自己必须时刻做出这些决定。 每当您在餐厅用餐时,您都必须决定要吃什么菜。 您应该去尝试已经尝试过并且知道自己喜欢的那道菜吗? 还是您会尝试另一道菜? 您有机会找到新的最爱菜,或者后悔没有选择更安全的菜。 这就是所谓的勘探开发困境。
勘探开发困境 (The Exploration-Exploitation Dilemma)
This dilemma is presented every time an agent wants to optimize an interaction with an unknown (and even partially known) environment. The agent wants to act as optimally as possible, but doesn’t know which action is optimal because doesn’t have full knowledge of which action is best for him. The only way to act optimally is by acting sub-optimally enough to understand the environment. By exploring, we learn more about our environment, but sacrifice the chance of getting a known reward. By exploiting, we use our current knowledge to obtain the best results, but risk acting sub-optimally by not knowing enough. This dilemma is present on almost every real-life situation we encounter with Reinforcement Learning. Developing good strategies for dealing with it is crucial, and that’s exactly what we’re going to do here.
每当代理想要优化与未知(甚至部分已知)环境的交互时,都会出现此难题。 代理希望尽可能地采取最佳行动,但不知道哪种行动是最佳的,因为他不完全了解哪种行动最适合他。 采取最佳行动的唯一方法是采取足够次佳的行动来理解环境。 通过探索,我们可以更多地了解我们的环境,但是却牺牲了获得知名奖励的机会。 通过利用,我们利用当前的知识来获得最佳结果,但是由于对知识的了解不足,可能会采取次优的行动。 我们在强化学习中遇到的几乎每个现实情况都存在这种困境。 制定应对策略的关键是至关重要的,而这正是我们在这里要做的。
评估我们的行动 (Evaluating our actions)
Before we start presenting strategies, we need to know how we’re going to evaluate our actions. A good way of looking at this is by seeing how we evaluate the dishes of a restaurant.
在开始提出策略之前,我们需要知道我们将如何评估我们的行动。 了解这一点的一种好方法是查看我们如何评估餐厅的菜肴。
Every time we get a dish, we evaluate how good our choice was. Is it tasty? How satisfied was I with the food? To each plate, we assign some value that indicates how good that choice was for us. This value gets updated every time we choose the dish. Dishes we often choose we’ll end up converging to an average satisfaction score.
每次我们得到一道菜,我们都会评估自己的选择有多好。 好吃吗? 我对食物有多满意? 我们为每个盘子分配一些值,该值表明该选择对我们有多好。 每当我们选择菜肴时,此值都会更新。 我们经常选择的菜式最终会收敛到平均满意度得分。
This is the same way an agent can evaluate their actions. In our scenario, for each arm we can pull from the multi-armed bandit, we have a value of what we expect to receive from such action. At first, we know nothing, and therefore expect nothing, but every time we take an action, we update our expectations.
这与代理评估其行为的方式相同。 在我们的方案中,对于我们可以从多臂匪徒身上拉出的每一只胳膊,我们都有从这种行动中期望得到的价值。 最初,我们一无所知,因此一无所知,但是每次我们采取行动时,我们都会更新期望值。
For example, let’s suppose we pull the first arm 5 times. For our behavior we receive this list of rewards.
例如,假设我们拉动第一只手臂5次。 对于我们的行为,我们会收到此奖励列表。

The expected value for that arm is, therefore, the average of all the values we’ve seen so far.
因此,该机械臂的期望值是我们到目前为止所看到的所有值的平均值。

So from our previous interaction, we’d expect to obtain a reward of 4.954. If we then pull the arm one more time, we need to calculate the average again. This can get tedious and unpractical if we had to store all the previously seen rewards for all the possible actions. We can do better by reformulating the average function to an update rule. After some wriggling around, we get:
因此,从我们之前的互动中,我们期望获得4.954的奖励。 如果再拉动手臂一次,则需要再次计算平均值。 如果我们必须为所有可能的动作存储所有先前看到的奖励,这将变得乏味且不切实际。 通过将平均函数重新格式化为更新规则,我们可以做得更好。 经过一番摸索 ,我们得到:

In English, this means that whenever we want to update the value of an action, we take our previous expectation and add the difference between the reward we expected and the reward we obtained, divided by the number of times we’ve actually taken that action. For example, if we pull the first arm for the sixth time, and obtain a reward of 5.18, then we can calculate our new expected value as:
用英语来说,这意味着每当我们想要更新一个动作的价值时,我们都会采用之前的期望,并加上期望的收益与获得的收益之间的差,除以我们实际采取该行动的次数。 例如,如果我们第六次拉动第一臂,并获得5.18的报酬,那么我们可以将新的期望值计算为:

We would do this for every action we have available. Notice that the update rule will end up converging as we increase the number of times we take an action. This is because as n gets larger, the value changes less and less.
我们将针对我们可用的每一项操作执行此操作。 请注意,随着我们增加执行操作的次数,更新规则最终将收敛。 这是因为随着n的增大,该值的变化越来越小。
贪婪的特工 (The Greedy Agent)
Our first strategy will be solely focused on exploitation. The greedy agent will always choose the best action according to its current knowledge. That is, the agent will always choose the action that has the current maximum expected value. So, if for example, this is the list of values our agent has calculated for each action, it would then select action 1:
我们的第一个策略将完全集中在剥削上。 贪婪的代理将始终根据其当前知识选择最佳操作。 即,代理将始终选择具有当前最大期望值的操作。 因此,例如,如果这是我们的代理为每个操作计算的值的列表,则它将选择操作1:

This can be expressed mathematically as taking the argmax of the expected values. If two or more actions are considered best (that is, they have the same value, and that value is the greatest overall actions), then the agent chooses randomly among those actions. For example, here it would go for either action 1 or action 3 randomly:
这可以在数学上表示为期望值的argmax 。 如果两个或多个动作被认为是最好的(即,它们具有相同的值,并且该值是最大的整体动作),则代理将在这些动作中随机选择。 例如,这里将随机执行动作1或动作3:

This behavior for the argmax function is not the default, so we need to write our own function that can break ties arbitrarily.
argmax函数的这种行为不是默认行为,因此我们需要编写自己的函数,该函数可以任意打破联系。
def argmax(q_values):
# Generate a mask of the max values for each row
mask = q_values == q_values.max(axis=0)
# Generate noise to be added to the ties
r_noise = 1e-6*np.random.random(q_values.shape)
# Get the argmax of the noisy maximum q_values
return np.argmax((q_values + r_noise)*mask,axis=1)Now, all we need to do is implement our greedy agent. For this, we need to specify how the agent takes an action, and how the agent learns from the interaction. As explained above, the agent takes an action based on which action yields the greatest expected value. On the other hand, it learns by updating the values for each action using the incremental average update rule.
现在,我们需要做的就是实现我们的贪婪代理。 为此,我们需要指定代理如何采取行动,以及代理如何从交互中学习。 如上所述,代理采取行动,基于该行动产生最大期望值。 另一方面,它通过使用增量平均更新规则来更新每个操作的值来进行学习。
class GreedyAgent:
def __init__(self, reward_estimates):
"""
Our agent takes as input the initial reward estimates.
This estimates will be updated incrementally after each
interaction with the environment.
"""
assert len(reward_estimates.shape) == 2
self.num_bandits = reward_estimates.shape[1]
self.num_experiments = reward_estimates.shape[0]
self.reward_estimates = reward_estimates.astype(np.float64)
self.action_count = np.zeros(reward_estimates.shape)
def get_action(self):
# Our agent is greedy, so there's no need for exploration.
# Our argmax will do just fine for this situation
action = argmax(self.reward_estimates)
# Add a 1 to each action selected in the action count
self.action_count[np.arange(self.num_experiments), action] += 1
return action
def update_estimates(self, reward, action):
# reward is a matrix with the obtained rewards from our previuos
# action. Use this to update our estimates incrementally
n = self.action_count[np.arange(self.num_experiments), action]
# Compute the difference between the received rewards vs the reward estimates
error = reward - self.reward_estimates[np.arange(self.num_experiments), action]
# Update the reward difference incementally
self.reward_estimates[np.arange(self.num_experiments), action] += (1/n)*errorBefore we run any tests, how do we expect our agent to do on this task? At first, our agent has no knowledge of the world, and so expects the same for every action. After the first action taken, one of two things can happen: The agent either loses money (negative reward) or gets a profit (positive reward). If the agent loses money, then it will consider the action taken as a bad action, and choose another one. If, on the latter, it wins money, the expectation of such action increases, and becomes the greatest action of all. This means that it will continue taking that action unless he loses sufficient money for the action to look bad.
在运行任何测试之前,我们希望我们的代理如何完成此任务? 起初,我们的代理人不了解世界,因此期望每个动作都一样。 在采取第一个操作后,可能会发生以下两种情况之一:代理人亏钱(负奖励)或获得利润(正奖励)。 如果代理人赔钱,则它将认为采取的措施是错误的措施,然后选择另一种措施。 如果就后者而言,它赢得了金钱,那么对这种行动的期望就会增加,并成为所有人中最大的行动。 这意味着它将继续执行该操作,除非他损失了足够的钱以使该操作看起来很糟糕。
Going back to our restaurant example, a greedy customer tries a dish, and if he likes it, he will only order that dish for the rest of his life. Only if the customer has sufficient bad experiences to dislike the dish, will he ever try another plate.
回到我们的餐厅示例,一个贪婪的顾客尝试一道菜,如果他喜欢,他将在余生中点这道菜。 只有当顾客有足够的不愉快的经历使他不喜欢这道菜时,他才会尝试另一盘。
Do you think this is a good strategy for getting the best outcome possible? Our agent will certainly not do badly, but it will also not do the best. It would be very lucky for our agent to land on the best possible action, and not another one that may look good. Let’s test it out!
您是否认为这是获得最佳结果的好策略? 我们的经纪人当然不会做得不好,但也不会做得最好。 对于我们的经纪人来说,能够采取最佳行动是非常幸运的,而不是另一个看起来不错的行动。 让我们测试一下!
# Initialize the environment of our multi-armed bandit problem
num_experiments = 2
num_bandits = 8
means = np.random.normal(size=(num_experiments, num_bandits))
stdev = np.ones((num_experiments, num_bandits))
env = ArmedBanditsEnv(means, stdev)
# Initialize the agent
agent = GreedyAgent(np.zeros((num_experiments,num_bandits)))
# Make a loop where the agent interacts with the environment
steps = 1000
for _ in range(steps):
action = agent.get_action() # Get the action chosen by the agent
_, reward, _, _ = env.step(action) # Interact with the environment
agent.update_estimates(reward, action) # Learn from interactionThe code above implements the interaction between the agent and the environment. The agent has 1,000 attempts to obtain as much reward as it can. Let’s see how this interaction goes. Below you’ll find 6 different agents interacting with 6 different environments. The environment consists of 8 individual actions (or armed-bandits) the agent can take. The red dots indicate the true expected value for each action, while the blue bars show the estimated value by the agent.
上面的代码实现了代理与环境之间的交互。 代理商尝试了1,000次,以获取尽可能多的报酬。 让我们看看这种互动如何进行。 在下面,您将找到6个不同的代理与6个不同的环境进行交互。 该环境由业务代表可以采取的8种单独行动(或武装匪徒)组成。 红点表示每个操作的真实期望值,而蓝条则表示代理商的估计值。



As you may see, exploration is not the main goal of our agent. The agent only explores a new action if all the others look worse than it. Some times our agent gets lucky, and lands on the highest valued action (like the fifth agent) but most of the times it ends up in a sub-optimal action. In fact, sometimes our agent was so unlucky that when it interacted with the correct choice, it received a bad outcome! Look at the fourth agent, it interacted with action 0, which is the best action, but got a loss out of it. After that, there’s not a chance our agent will ever try that action again, even though it would cause higher average rewards than any other action!
如您所见,探索不是我们代理商的主要目标。 如果其他所有动作看起来都比它糟糕,则该代理仅探索新动作。 有时,我们的特工很幸运,并着手进行价值最高的行动(如第五特工),但大多数情况下,它最终以次优的行动而告终。 实际上,有时我们的代理人很不幸,以至于当它与正确的选择进行交互时,都会收到不好的结果! 看第四个特工,它与动作0相互作用,这是最好的动作,但失败了。 在那之后,我们的经纪人再也没有机会再次尝试该操作了,即使它会比其他任何操作带来更高的平均奖励!
We just saw a few agents using the greedy strategy, and it doesn’t look good. But how does it behave overall? We can actually do a lot of experiments and observe the average behavior.
我们只是看到一些特工使用贪婪策略,但效果并不理想。 但是,整体表现如何? 实际上,我们可以进行大量实验并观察平均行为。

The above graph displays an average over 10,000 individual experiments of the percentage of times an agent took the optimal action (that is, the best action on the environment). The above plot indicates that on average, 40% of the time our greedy strategy landed us on the optimal action. We can also conclude that after a few attempts, the agents didn’t get any better. Only the first dozen attempts matter to our agent, since after that it will usually stick to a single action. Clearly, pure exploitation techniques are far from being optimal. What if we introduce some exploration?
上图显示了平均10,000个以上的单个实验,以了解代理采取最佳行动(即对环境的最佳行动)的次数百分比。 上面的图表明,平均而言,我们的贪婪策略有40%的时间使我们处于最佳行动上。 我们还可以得出结论,经过几次尝试,代理商并没有得到任何改善。 仅前十次尝试对我们的代理人很重要,因为在此之后,它通常只会执行一次操作。 显然,纯粹的开采技术远非最优。 如果我们进行一些探索该怎么办?
贪婪的代理商 (The ɛ-greedy Agent)
This new strategy adds a little bit of randomness to the action selection process. In general, the agent behaves just as the Greedy Agent seen above. But, every once in a while, it will choose an action at random. The probability of our agent taking a random action is determined by a new parameter called epsilon (ɛ). Epsilon is, therefore, a value between 0 and 1.
这种新策略为动作选择过程增加了一些随机性。 通常,该代理的行为与以上所示的贪婪代理相同。 但是,它偶尔会随机选择一个动作。 我们的代理采取随机行动的可能性由一个称为epsilon(ɛ)的新参数确定。 因此,Epsilon的值在0到1之间。
The way this works is that every time our agent wants to take an action, it kind of “rolls a dice”, and based on the outcome it decides whether to act greedily or randomly. For example, if ɛ is assigned to 1/6, then it would be equal to saying that whenever the agent rolls a 1 on the dice, it will act randomly. Here’s our new implementation of the agent:
这种工作方式是,我们的代理人每次要采取行动时,都会“掷骰子”,并根据结果决定是贪婪地行动还是随机行动。 例如,如果将ɛ分配给1/6,则等于说代理在骰子上每掷1便会随机行动。 这是我们对代理的新实现:
class EpsilonGreedyAgent(GreedyAgent):
def __init__(self, reward_estimates, epsilon):
GreedyAgent.__init__(self, reward_estimates)
# Store the epsilon value
assert epsilon >= 0 and epsilon <= 1
self.epsilon = epsilon
def get_action(self):
# We need to redefine this function so that it takes an exploratory action with epsilon probability
# One hot encoding: 0 if exploratory, 1 otherwise
action_type = (np.random.random_sample(self.num_experiments) > self.epsilon).astype(int)
# Generate both types of actions for every experiment
exploratory_action = np.random.randint(self.num_bandits, size=self.num_experiments)
greedy_action = argmax(self.reward_estimates)
# Use the one hot encoding to mask the actions for each experiment
action = greedy_action * action_type + exploratory_action * (1 - action_type)
self.action_count[np.arange(self.num_experiments), action] += 1
return actionWe’re actually basing the agent on the Greedy implementation, and only changing how the agent chooses the actions to take.
实际上,我们实际上是基于Greedy实现来创建代理,并且仅更改代理选择采取行动的方式。
Now our agent will allow some exploration, but the amount of exploration is based on what number we assign to ɛ. If epsilon is 0, then our agent will act just as the Greedy implementation. If, on the other hand, epsilon is 1, then our agent is nothing more than a random machine. For now, we’ll go with an epsilon value of 0.1, but later on we’ll explore other values. Our agent will therefore act greedily 90% of the time, and exploratory just 10%.
现在我们的代理将允许进行某些探索,但是探索的数量取决于我们分配给ɛ的编号。 如果epsilon为0,则我们的代理将充当Greedy实现。 另一方面,如果epsilon为1,那么我们的代理人就是随机机器。 现在,我们将使用epsilon值0.1,但是稍后我们将探索其他值。 因此,我们的代理人将有90%的时间贪婪地行事,而探索性的时间只有10%。
Let’s see this strategy in action:
让我们看看这个策略的实际效果:
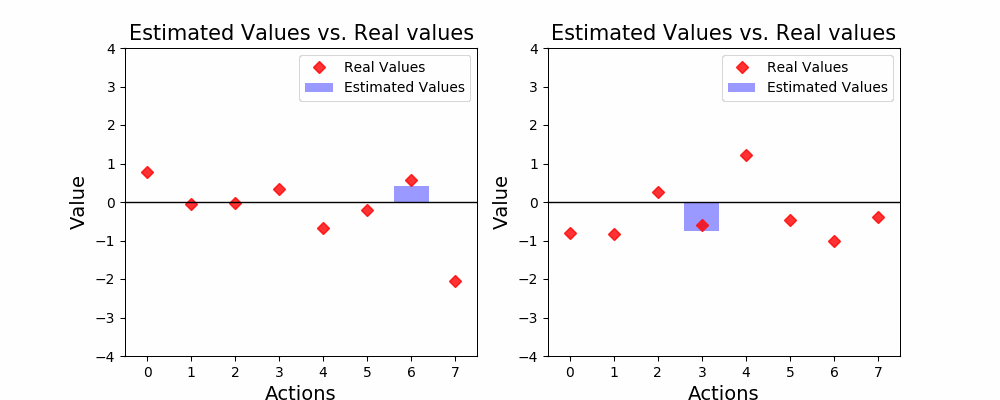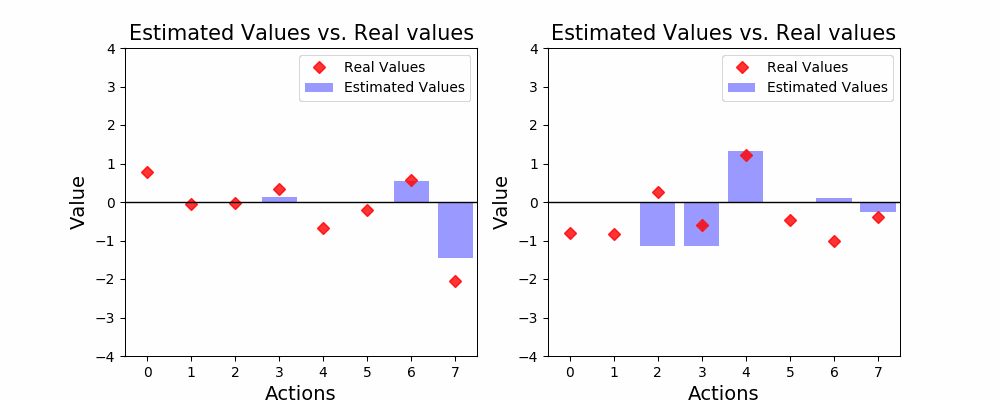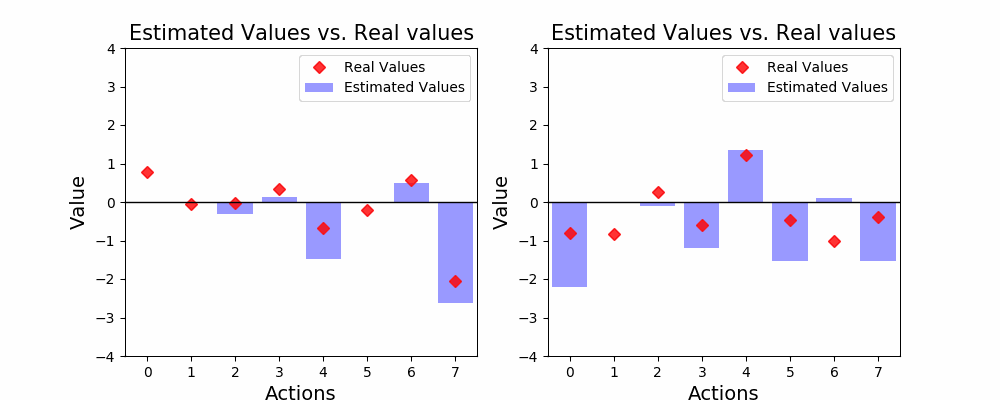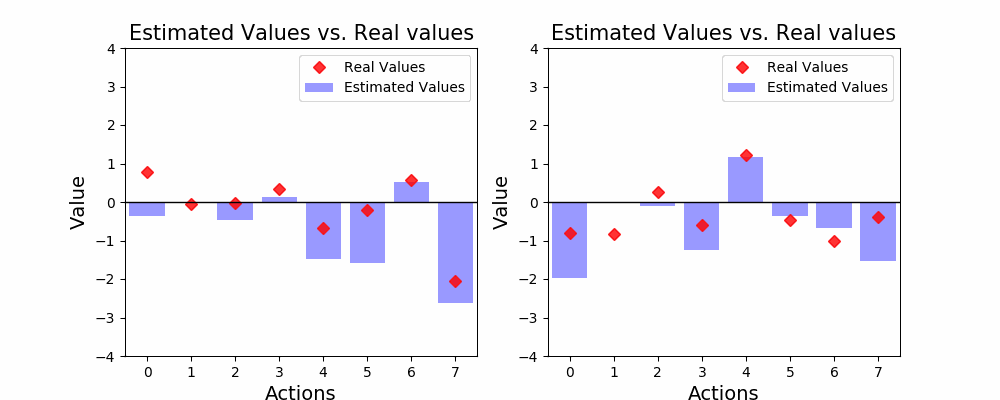


Things are starting to look promising! In almost all of the examples above our agent was able to find the optimal action. In fact, given enough time, our agent will end up finding out a good estimated value for all of the actions. Notice how the blue bars now show values closer to the red dots? Our agent can now be confident enough that it knows which action is optimal. Again, let’s see how this strategy looks on average:
事情开始看起来很有希望! 在以上几乎所有示例中,我们的代理都能找到最佳行动。 实际上,如果有足够的时间,我们的代理商最终将为所有行动找到一个好的估算值。 请注意,蓝色条现在如何显示更接近红点的值? 现在,我们的代理人可以足够自信地知道哪个操作是最佳的。 再次,让我们看看这种策略的平均表现:

The ɛ-greedy Agent does much better compared to the greedy strategy! After 1,000 steps, the ɛ-greedy strategy manages to get close to choosing the right action 80% of the times. Also, we see how this strategy increases it’s optimality over time, which means that it is always learning from interaction.
与贪婪策略相比,ɛ-贪婪代理的性能要好得多! 经过1,000步后,“贪婪”策略设法接近80%的时间选择正确的操作。 另外,我们看到了这种策略如何随着时间的推移提高其最优性,这意味着它始终在从交互中学习。
So, what value should we choose for ɛ? Well, let’s test multiple values of epsilon to see how much reward they obtain on average:
那么,我们应该为choose选择什么值? 好吧,让我们测试epsilon的多个值,看看它们平均可获得多少奖励:

Here, we see that the best value for epsilon in this scenario is 0.1. The reason is because it is small enough to allow our agent to mostly behave greedily, and so prioritize high rewards, but big enough to allow our agent to explore the environment quickly. Higher values of epsilon will start getting in the way of our agent, since time exploring is time not obtaining high rewards. Lower values mean our agent will take longer to understand the environment, which means it could take a long time before it finds the optimal action.
在这里,我们看到在这种情况下epsilon的最佳值为0.1。 原因是因为它足够小,可以让我们的特工大体上表现出贪婪的行为,因此优先考虑高额的奖励,但又足够大,可以让我们的特工快速探索环境。 较高的epsilon值将开始妨碍我们的代理商,因为时间探索是无法获得高回报的时间。 较低的值表示我们的代理将花费更长的时间来了解环境,这意味着找到最佳的动作可能需要很长时间。
结语 (Wrapping Up)
So far, we’ve presented a situation where a dilemma between acting optimally and exploratory emerges. We’ve seen how such a dilemma can drastically affect how we learn and interact with an environment. Based on this situation, we’ve defined some ways in which our agent can evaluate its actions, as well as learn from the environment. This article finishes exposing and comparing two strategies for dealing with the Exploration-Exploitation dilemma, namely the Greedy Agent and the ɛ-Greedy Agent. The idea behind these strategies will be present throughout our journey into Reinforcement Learning, and understanding the concepts behind them, as well as their strengths and weaknesses will serve us later on.
到目前为止,我们已经提出了一种情况,在这种情况下,最佳行动和探索之间会出现困境。 我们已经看到了这样的困境如何能够极大地影响我们学习和与环境互动的方式。 根据这种情况,我们定义了代理可以评估其行为以及从环境中学习的一些方法。 本文完成了对“探索-开发”困境的两种策略,即贪婪代理和ɛ-贪婪代理的阐述和比较。 这些策略背后的思想将在我们进入强化学习的整个过程中呈现出来,理解它们背后的概念以及它们的优缺点将在以后为我们服务。
In the next article, we’ll explore what happens to our strategies when they are used in non-stationary environments. That is, when the average reward received from our actions isn’t static, but instead is slightly changing whenever our agent interacts with it. We will therefore present some modifications that can make our agents behave better in such situations. Give yourself a pat on the back if you made it this far. This was not an easy read, and I hope you learned something along the way.
在下一篇文章中,我们将探讨在非固定环境中使用策略时会发生什么情况。 也就是说,从我们的行为获得的平均报酬不是一成不变的,而是每当我们的代理与之交互时,它就会略有变化。 因此,我们将提出一些修改,这些修改可以使我们的代理在这种情况下表现更好。 如果您走了那么远,请拍一下自己的背。 这不是一本容易读的书,希望您在此过程中学到一些东西。





















 1275
1275

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








