三位数的茎叶图怎么看_苏教版四年级数学上册第二单元、两、三位数除以两位数（2.4~2.10）微课视频 | 练习...

在小学学习中，关键点就是积累足够多的基础知识，为今后更高级的学习奠定基础。今天小学基础知识库就为大家分享 苏教版四年级数学上册第二单元、两、三位数除以两位数(2.4~2.10)微课视频 | 练习 ， 希望对老师教学和孩子学习有所帮助。欢迎大家转发、分享、收藏哦~ 更要在图文右下角点在看！！！ 往期回顾

苏教版四年级数学上册电子课本

第一单元、升和毫升

第1课、升和毫升(1)

第2课、升和毫升(2)

第3课、升和毫升(3)

第二单元、两、三位数除以两位数

第4课、除数是整十数的口算和笔算

第5课、三位数除以整十数的估算和笔算

第6课、除数是整十数除法应用

2.4《用“四舍五入”法试商》

同步练习

1．填一填。

(1)计算866÷79时，可以把除数看作(　　)来试商，商是(　　)位数。

(2)336÷48，计算时可以把除数看作(　　)来试商，商应该写在(　　)位上。

2.列竖式计算。

384÷21         298÷42          378÷23         289÷17

3某超市8月分销售了899千克的西瓜，平均每天销售多少千克西瓜？

参考答案

 1.(1)80  两  (2)50   个

2.18……6      7……4     16……10    17

3.899÷31=29(千克)答：平均每天销售29千克西瓜。

教学设计

教材第12~14页的内容。

1.在具体情境中,经历两、三位数除以两位数试商方法的探索过程,会运用“四舍五入”法进行试商,并能正确地笔算除数是两位数(商是一位数)的除法。

2.在探索计算方法和解决问题的过程中,感受数学与生活的联系,增强自主探索的意识,提高合作交流的能力,增强应用数学的意识,获得积极的数学学习情感。

重点:掌握两、三位数(非整百整十数)除以两位数(非整十数)的笔算。

难点:运用“四舍五入”法试商。

课件、配套光盘。

1.说一说下面的数最接近哪个整数。

21≈39≈57≈64≈

23≈        31≈               96≈          48≈

2.计算并验算。(计算前先估计结果)

96÷1995÷3175÷24

432÷64          390÷44        810÷79

3.根据上题,讨论一下如何估算最合理。

1.例题讲解。

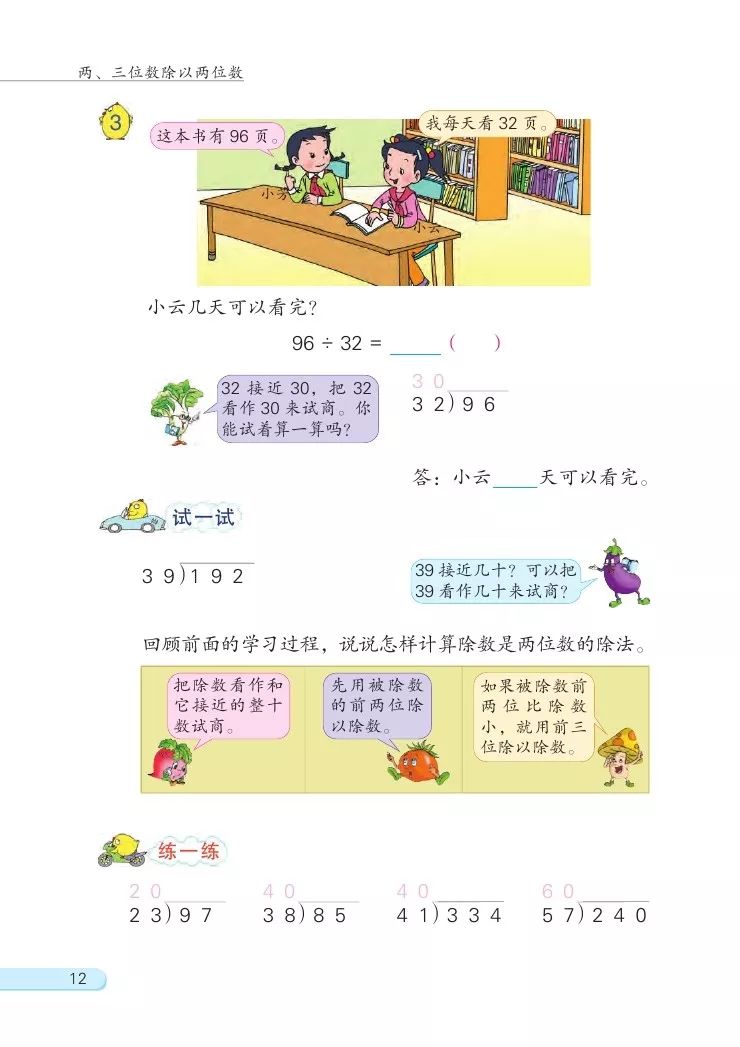
(1)出示教材第12页例3,教师拿一本书作教具。

老师手里的书共96页,现在老师决定每天看30页。你认为我能看几天,还剩多少页?

①让学生理解题意后列式计算,并订正结果。

96÷30=3(天)……6(页)

②如果老师决定每天看32页,你认为老师能看几天?还有没有余下的页数?

请同学们先列出算式,不要解答。

96÷32

③学生列出式子后,引导学生观察除数和刚才的除数有什么不同,引出课题。讨论可以把32看作几十来试商。32接近30,把32看作30来试商,这是“四舍”法试商。

验算一下,看看算得对不对。

④教学教材第12页“试一试”。

39接近40,把39看作40来试商,这是“五入”法试商。

(2)出示课件。

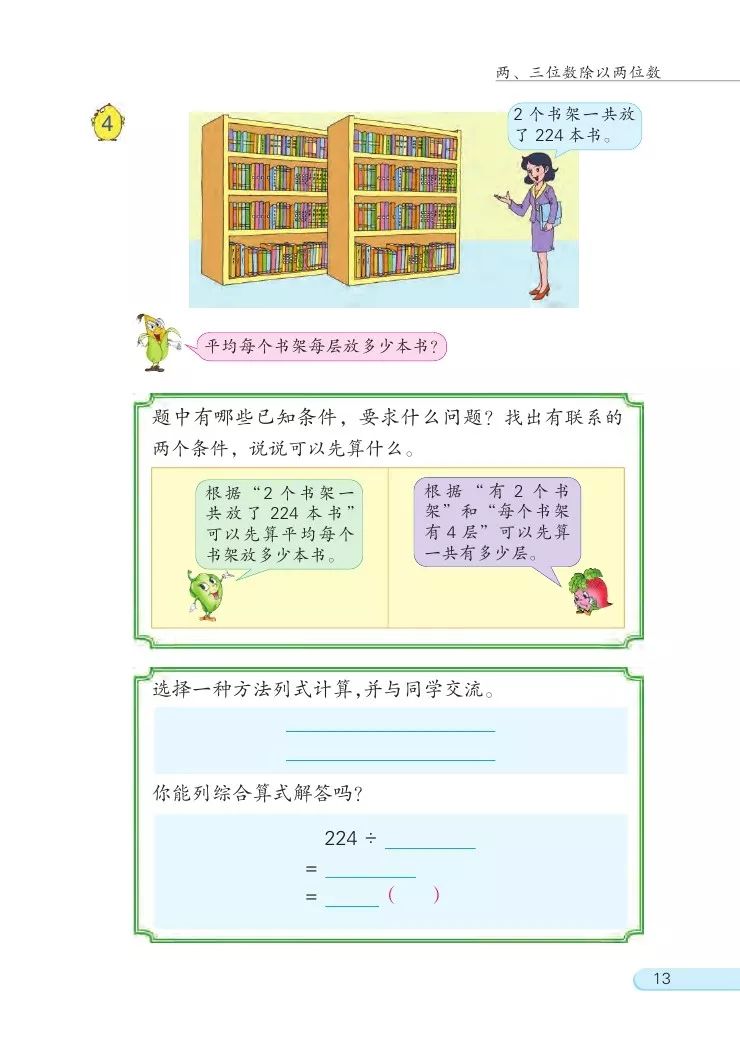
平均每个书架每层放多少本书?

①已知条件:两个书架,每个书架4层,一共放了224本书。

②解题思路:可以先算平均每个书架放了多少本书,也可以先算一共有多少层。

方法一:两个书架,一共224本书,则每个书架放224÷2=112(本);每个书架4层,一共放112本书,则每层放112÷4=28(本)。列综合算式:224÷2÷4=28(本)

方法二:两个书架,每个4层,则两个书架共4×2=8(层);8层,一共224本书,则每层放224÷8=28(本)。

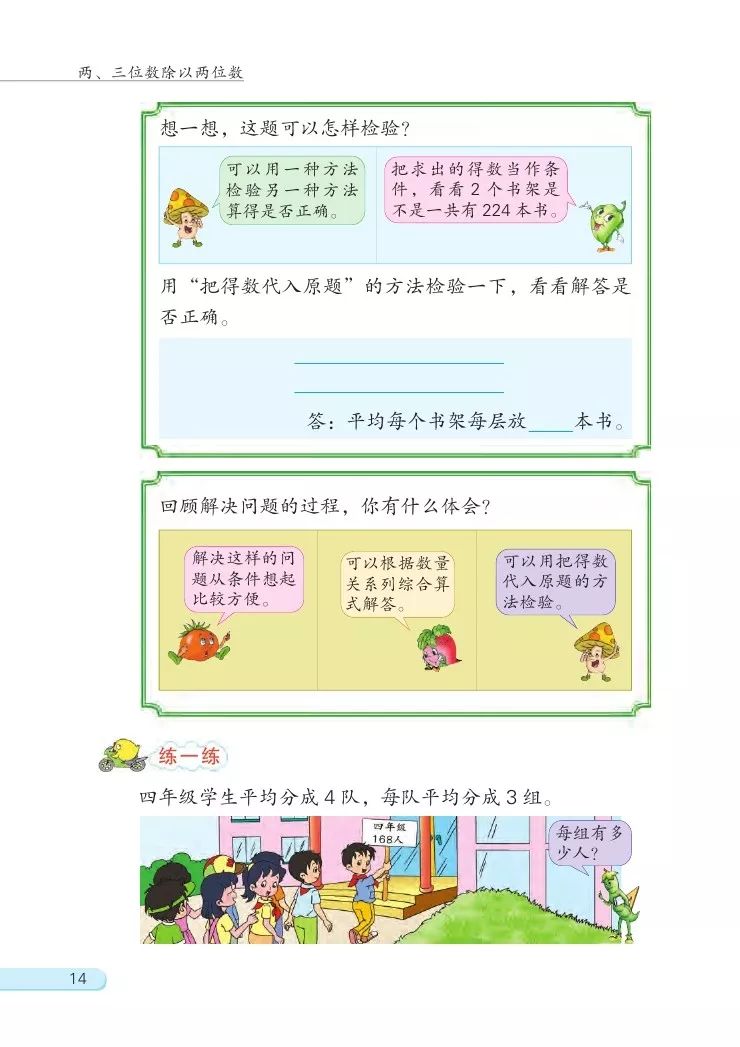
③检验:想一想,这题可以怎样检验?

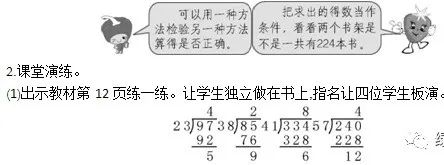
引导学生用“四舍五入”法试商,题中除数23可看作20,38可看作40,41可看作40,57可看作60。

(2)出示教材第14页练一练。先让同桌间讨论,然后让学生在练习本上完成。

168÷4÷3=14(人)

2.5《连除的实际问题》

同步练习

 1.小华、小芳和小英6天一共写了360个毛笔字，平均每人每天写多少个？

(1)可以先计算出平均每天3人写了多少个毛笔字，可列式：(         )，再计算平均每天写多少个，列式为(          )。

(2)也可以先计算出平均每人6天写多少个毛笔字，列式：(        )，再计算平均每天写多少个，列式为(          )。

2.把问题和相对应的算式连起来。

每盒有20个面包，明明买了4盒，共花了240元。

每盒面包多少元？                20×4

每个面包多少钱？               240÷4

4盒面包一共有多少个？          240÷4÷20

3.小红买了两盒饼干，一共重1千克，每盒有25块饼干，每块饼干重多少克？

参考答案

教学设计

教材第15~17页的内容。

1.巩固笔算两、三位数除以两位数的试商方法,熟练掌握试商的基本方法,提高学生试商的水平。

2.在试商的基础上让学生学会基本的计算方法。

3.联系生活实际,综合不同内容的知识,让学生解决简单的实际问题。

重点:熟练掌握两、三位数除以两位数的试商方法。

难点:进一步提高学生的试商水平,以试商为基础解决实际问题。

口算卡、课件、配套光盘。

用竖式计算。

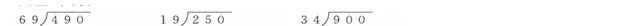
1.基础练习。

(1)出示练习三第1题,指名让学生在黑板上演示计算过程,然后集体订正,让学生口述验算过程。

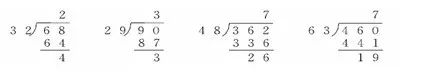
(2)出示练习三第2题。

一部儿童电视剧共要播放288分,每天从17:00播放至17:32,多少天可以播放完?

分析:电视剧每天播放的时间为17:00~17:32,共32分。

电视剧总长为288分,所以将整部电视剧播放完要用288÷32=9(天),在计算288÷32时,引导学生试商,可以把32看作30,用9试商。

(3)出示练习三第3题,指名让学生依次板演三位阿姨每天编织中国结的数量。

比较两个式子,可以发现被除数都是99,除数分别为33和38。在试商时,可以把33看作30,把38看作40,试商就变得简单易行了。以下三组式子也是相同的情况,引导学生仔细体会“四舍五入”法试商的算理,遇到非整十整百数的除法,学生试商时就可以做到游刃有余了。

(5)出示练习三第5题,让学生先说说各题的商是几位数,再计算。

判断商是几位数:笔算除法时,能够正确判断商是几位数对保证计算正确是很重要的。因为如果先确定商是几位数就能防止把商写错位置。提问:怎样能很快判断出商是几位数?商的位数与被除数位数有什么关系?(除数是两位数的除法,如果被除数的前两位够除,则商的位数等于被除数的位数减1;如果被除数的前两位不够除,则商的位数等于被除数的位数减2)

如:

 (6)出示练习三第6题,与学生一起分析应用题中的数量关系,每填一个空格,就是用一个数量关系式解决一个实际问题。接着,让学生独立解决问题。最后让学生交流解决问题的方法和结果。这样,不仅能使学生熟悉有关术语,理解和掌握数量关系式,还能使学生感知每种数量关系中只要知道其中的两个量,就可以求得另一个未知量,从而加深对每组数量中三个量之间关系的认识。

(7)出示练习三第7题,分步解决问题,首先计算剩下的花共有多少盆:160-28=132(盆);再计算这些花要平均分给22个班,每班分得几盆:132÷22=6(盆)。

引导学生阅读其他的问题,然后思考怎样解决问题,养成勤于练习的习惯。

2.总结规律。

教学时,应充分利用学生已有的知识和经验,放手让学生通过计算、观察和比较等活动去发现规律。同时,注意发挥教师的引导作用。

2.6《试商后需要调商的笔算除法(1)

同步练习

1.    填空。

(1)一个数除以43，把43看作(　　)来试商，发现乘积大于被除数，此时，要把商调(　　)。

(2)4□3÷53，要使商是9，□里可能填(　　　　)；要使商是8，□里可能填(　　　　　　　)。如果是7呢？□里可能填(　　　    )。

2.列竖式计算。

126÷14=        272÷34=          407÷82=      802÷12=

3.小红23天看完一本161页的课外书，她平均每天看几页？

参考答案

1.(1)40  小

(2)8、9     3、4、5、6    0、1、2

2.9   8     4……79     66……10

3.161÷23=7(页)答：她平均每天看7页。

教学设计

两、三位数除以两位数(可用“四舍”法、“五入”法试商并调商)

教材第18~19页的内容。

1.进一步提高学生计算两、三位数除以两位数时试商的能力,掌握初商后需要调商的试商方法。

2.进一步提高学生对初商调整的判断能力,逐步形成必要的技能。

3.运用有关除法计算解决简单实际问题。

4.更好地理解除法的笔算方法,提高推理能力,激发学生学习数学的兴趣。

重点:掌握除数是两位数的除法中试商时的调商(“四舍”法、“五入”法试商)。

难点:运用有关除法计算解决简单实际问题。

课件、配套光盘。

1.口算。

127÷41=907÷49=292÷28=

2.让学生口答这组题的试商结果,并说说自己是怎样想的。然后教师总结试商的方法。

1.出示教材第18页例5。

(1)刚才计算的几个小题除数都是接近整十数的数,41可以看作40,49可以看作50,28可以看作30。在计算过程中,只要试一次商就可以得到准确的得数。下面看一看这道例题。(教师出示例题)

四年级一班有34人,一共借书272本。四年级一班平均每人借书多少本?

师:请大家根据题意列出算式,272÷34。

师:同学们看一下这个式子中的除数,该把它看作多少来试商呢?

学生回答后,教师板书,与学生一起试商并发现问题。

师:把34看作30试商,9乘34得306,272比306小,怎么办?(把商调小,用8来试商)

让学生口算,教师板演。

(2)前边我们一起学了除数不接近整十数且个位数小于5时用“四舍”法试商及调商的方法,有另一种情况,除数是不接近整十的数,它的个位数大于5,如16、17、26、36,如果用“五入”法试商,有时商的数会偏小,需要调大后再试,直到得到准确的得数。下面用这种方法试着分析解答教材第19页例6:

四年级二班有36人,一共借书252本。四年级二班平均每人借书多少本?

师:同样是一道求平均数的实际应用题,请大家根据题意列出算式,252÷36。

师:如果把除数36看作40,口算可知应用6试商,大家讨论一下商6可以吗?为什么?(教师用6作商进行板演)

师:请大家比较前面两道例题计算中的相同点和不同点,然后大家交流一下。

2.小结。

在除数是两位数的除法中,当除数十位上的数较小,个位上又不接近整十数,如14、24、33,如果用“四舍”法把除数看作整十数来试商,商偏大,需要把商调小后再试,直到得出正确的得数。同理,如果除数是15、25、35这样的数,如果用“五入”法把除数看作整十数来试商,商偏小,需要把商调大后再试,直到得出正确结果。

3.课堂演练。

教材第18、19页练一练。调商的基本练习,用于巩固调商的方法。练习题给出首次试商的情况,让学生根据试商情况,说一说进一步如何调商。练习时,可以让学生交流一下教材首次试商的理由,然后根据每个小题具体调商并计算结果。

2.7《试商后需要调商的笔算除法(2)》

同步练习

1.    填空。

(1)            试商时，余数比除数大，应该把商调(   )。

=10……32，除数最小是()，这时被除数是()。

2.列竖式计算。

468÷78=        472÷59=          351÷39=        126÷18=

3.王阿姨10月份工作了28天，做了252个手工布偶，平均每天做多少个手工布偶？

参考答案

1.(1)大

(2)33  362

2.6   8    9   7

3.252÷28=9(个)答：她平均每天做9个手工布偶。

教学设计

1.通过练习进一步掌握算法,形成技能,达到会算和算对的要求。

2.进一步巩固计算方法,促进学生养成细致和认真的习惯。

3.提高学生解决实际问题的能力,培养良好的思维习惯。

重点:巩固计算方法,形成技能。

难点:提高学生解决实际问题的能力。

课件、配套光盘。

在前面的几节课,大家一起学习了两、三位数除以两位数的计算方法,请大家先回忆一下所学过的知识点,然后一起完成下面的练习题。

1.基础练习。

出示练习四第1题,算一算,比一比。指名让学生板演,让学生说说上下两题有什么不同之处。以第一组为例稍作讲解。

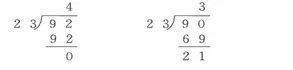
92÷23=4,商为整数,所以92可以被23整除;90比92小2,90不能被23整除,且商比4小,故用3试商,余数为21。

出示练习四第10题,三位数除以两位数的笔算及验算。出示第一个小题,指名让学生板演,计算并验算,集体订正。

商=被除数÷除数　　被除数=商×除数

出示练习四第11题,三位数除以两位数的估算及笔算。先让学生估计书中各题的商是几,再计算。交流一下如何试商和调商。

出示练习四第13题,实际应用题。教师可根据题意将题中的数量关系列出一个表格,然后让学生计算,把得数依次填入表中。

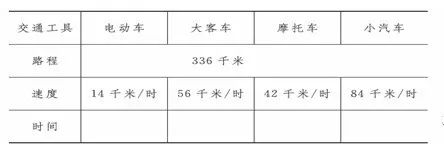
　　引出计算公式:路程=速度×时间　时间=路程÷速度　速度=路程÷时间

请你想一想,你还能提出用除法计算的其他问题吗?

出示练习四第15题,估计商的位数。以前两个小题为例,讲解三位数除以两位数时商是几位数的估计方法。

出示练习四第16题,估计商的最高位可能是几。与上题方法类似,教师可出示两个小题作详解,让学生交流计算方法。

出示练习四第19题,实际应用问题。分析题意,要想求出养鸡的只数是鸭的几倍,必须先求出一共养鸡多少只。由题中给出的条件可知,王大伯家养公鸡185只,母鸡229只,所以王大伯家一共养鸡185+229=414(只)。

王大伯家养鸭46只,求养鸡的只数是鸭的几倍:414÷46=9。

2.练习小结。

计算针对学生在练习过程中易出现的问题,教师进行简单的小结,使学生在计算中能够更正确地掌握计算方法。

3.课后练习。

将练习四的其他各题作为练习,留给学生在课后完成。

2.8《商不变的规律》

同步练习

参考答案

1.(1)不变

(2)除以2  

(3)除以3

2. 8  40  80

 180 36  18

3.18×6=108

教学设计

商不变规律的认识及应用

教材第23~24页的内容。

1.掌握被除数、除数和商之间的变化规律,能用简洁的语言表述三者间的变化规律。

2.用商不变的规律解决实际问题。

3.通过探索规律,培养认真观察的能力和语言表达的能力。

重点:能正确运用商不变规律进行简便计算。

难点:总结探索商不变规律的过程,培养探究和解决问题的能力。

课件,配套光盘。

1.口算。

6÷3=    8÷4=    15÷5=

60÷30=    80÷40=    150÷50=

2.算一算,比一比。

36÷18=         72÷36=         45÷15=

360÷180=         720÷360=         450÷150=

3.让学生对比上面两题的结果和算式,看看有什么发现。

1.例题讲解。

(1)导入中的算式题,答案都是一样的。但是,算式本身却存在很大的差别。想一想,这是为什么呢?带着疑问,我们来看教材第23页例题7。

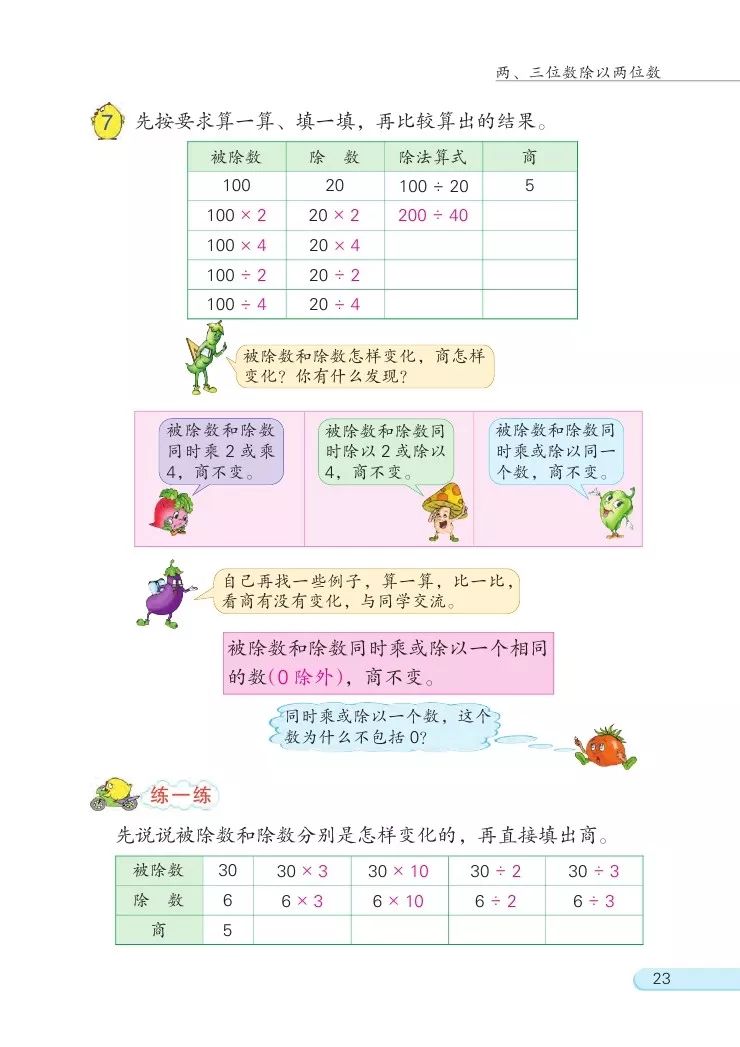
　　先按要求算一算、填一填,再比较算出的结果。

被除数	除数	除法算式	商
100	20	100÷20	5
100×2	20×2	200÷40
100×4	20×4
100÷2	20÷2
100÷4	20÷4

　　教师:请同学们在草稿纸上,先完成表格,然后同桌之间进行交流讨论。看一看,想一想,被除数和除数是怎样变化的?商有没有变化?有什么发现呢?

学生汇报交流结果。

观察表格,我们发现被除数和除数同时乘2或乘4,商不变。被除数和除数同时除以2或除以4,商不变。因此我们说被除数和除数同时乘或除以一个相同的数,商不变。因为0不能作除数,所以0除外。

师:好的,回答得非常正确!把刚才的发现,用一句话总结就是:

教师总结:被除数和除数同时乘或除以一个相同的数(0除外),商不变。

(2)根据前面的总结,我们再看下面的题目。(出示课件)

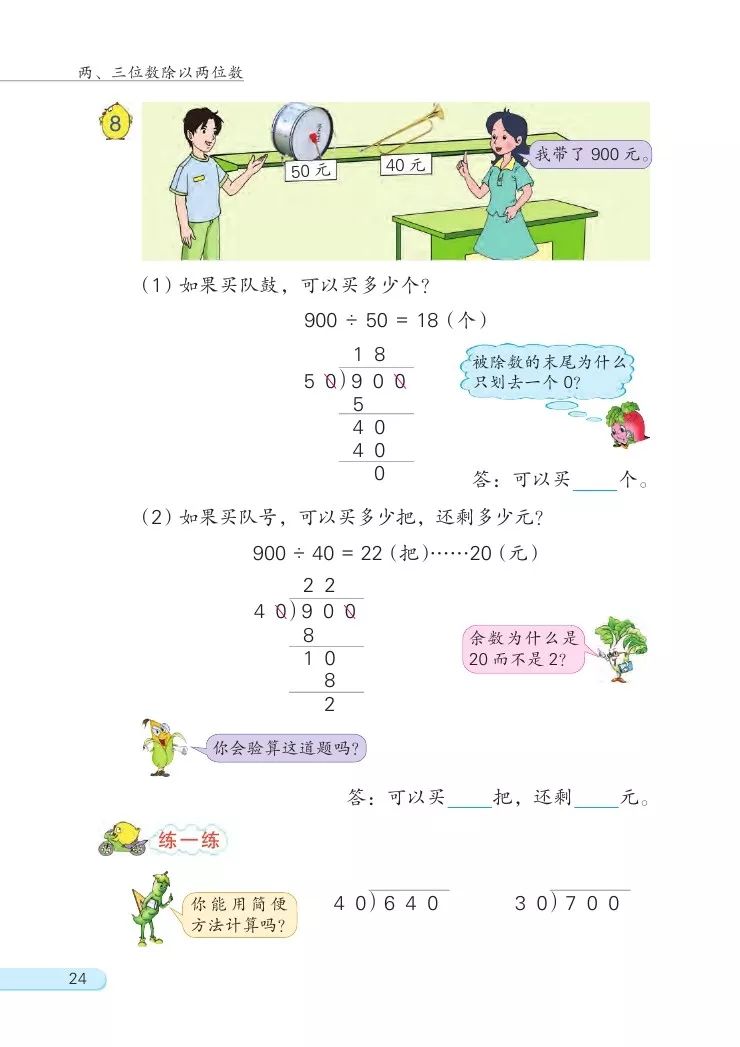
师:先看第一个问题,如果买队鼓,可以买多少个?

生:已知队鼓50元一个,一共有900元钱,问可以买多少个,用除法计算,列式为900÷50。

师:好的,根据商不变的规律,这个算式有没有简算的方法呢?

生:有,被除数和除数同时除以10。

教师板书:900÷50=(900÷10)÷(50÷10)=90÷5

师:相应地,在竖式计算的过程中,我们是不是也可以简化呢?

学生讨论,教师板书。

900÷50=18(个)

师:好的,再看第二个问题,如果买队号,可以买多少把,还剩多少元?同学们试着完成一下,要注意验算。

指名板演,教师巡视,指导个别有困难的学生。

900÷40=22(个)……20(元)

2.例题小结。

用简便方法计算被除数和除数末尾有0的有余数除法时,被除数和除数末尾同时划去了几个0,就在余数末尾添上几个0。

3.课堂演练。

(1)根据240÷60=4,直接写出下列各式商,你发现了什么?

2400÷600=480÷120=1200÷300=

120÷30=  24÷6=       48÷12=

最后结果都等于4,再次证明了商不变的规律。

(2)每把椅子的售价是30元,小明的爸爸带了1200元,可以买多少把椅子?

1200÷30=40(把)

答:可以买40把。

2.9《商不变的规律的应用》

同步练习

1.    直接写出得数。

160÷40=           280÷40=          560÷70=    

720÷40=           230÷30=          490÷40=

2.列竖式计算，并验算。

400÷80                650÷40              670÷30

3.养鸡场有720只母鸡，有60只公鸡，养殖场母鸡的数量是公鸡的多少倍？

参考答案

1.4  7  8  18    7……20    12……10

2.50    16……10    22……10

3.720÷60=12答：养殖场母鸡的数量是公鸡的12倍。

教学设计

教材第25~26页的内容。

1.巩固商不变规律的认识及应用,加深理解并熟练掌握商不变的规律。

2.灵活运用商不变规律进行简便计算,提高解决问题的能力。

3.联系生活实际,综合解决两、三位数除以两位数的实际问题。

重点:理解并掌握商不变的规律。

难点:明晰算理,运用商不变的规律进行简便计算。

课件,配套光盘。

根据每列中第1题的商,写出下面几题的商。

24÷8=3  49÷7=7  18÷2=9

240÷80=         490÷7=           180÷2=

2400÷80=           4900÷70=        1800÷20=

2400÷800=         4900÷700=           1800÷200=

1.基础练习。

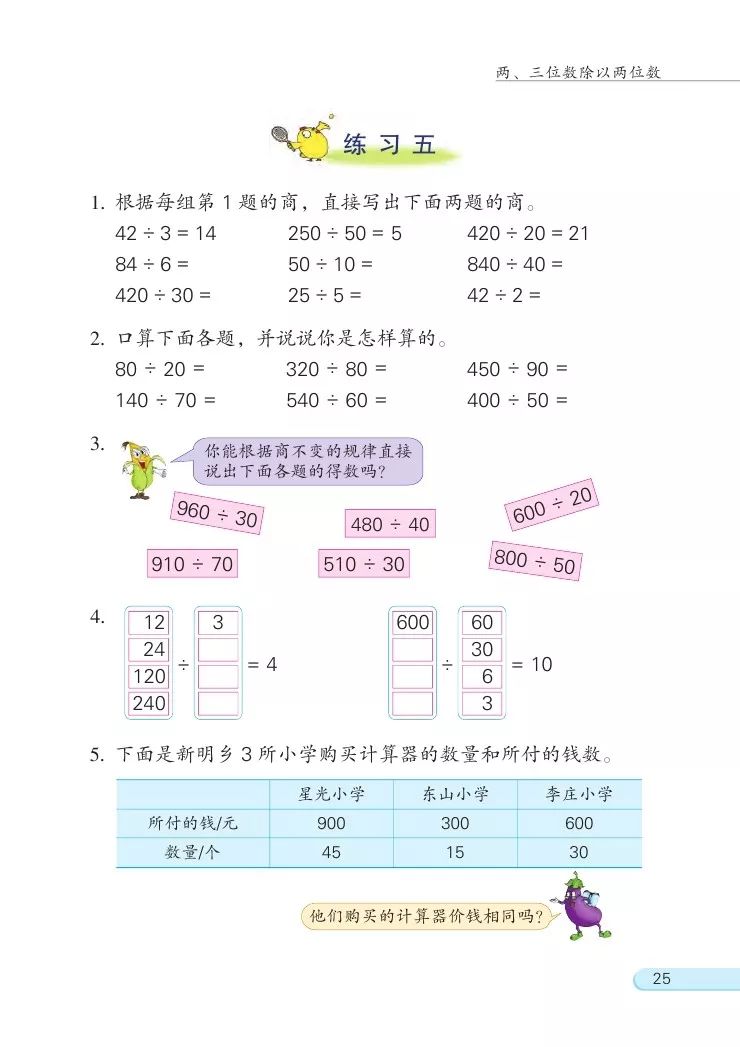
(1)出示练习五第1题。指名学生根据每组第1题的商,口述答案。

(2)出示练习五第2题。口算下面各题,并说说是怎样算的。

(3)出示练习五第3题。

分析:根据商不变的规律,被除数和除数末尾同时含有1个0,就可以同时除以10,可以直接说出下面各题的得数。

(4)出示练习五第4题。

分析:第一组已知被除数和商,求除数。由“被除数÷除数=商”可知,“被除数÷商=除数”。24÷4=6,120÷4=30,240÷4=60。

另外,观察算式可知,四个除式,商都是4,各被除数存在一定的倍数关系。根据商不变规律,要使商不变,被除数12乘或除以几(0除外),除数也要乘或除以一个相同的数。

让同学根据上面的讲解,独立完成第二组除式。

(5)出示练习五第5题。

分析:根据总价和数量,求出各个单价,再比较大小,先用除法计算。指名三位同学板演,然后集体订正。

(6)出示练习五第6题。

教师:请同学们在教材上完成填空,同桌之间进行交流讨论。看一看,想一想:被除数和除数是怎样变化的?商有没有变化?有什么发现呢?

(7)出示练习五第7题。

分析:用简便方法计算被除数和除数末尾有0的有余数除法时,被除数和除数末尾同时划去几个0,就在余数末尾添上几个0。第一个竖式中,同时去掉了一个0,因此余数应是20;第二个竖式中,同时去掉了两个0,因此余数应是200。

2.练习小结。

针对学生在练习中出现的问题,教师要及时指正和总结,并对可能犯的错误,要有预见地指出。使学生在今天的计算中,能更正确地掌握方法。

3.课后练习。

将练习五的其他各题作为练习,留给学生在课下完成。

2.10《简单的周期》

同步练习

参考答案

答：2019年国庆节是星期二。

3.77÷5=15(组)……2(颗)是白色。

68÷5=13(组)……3(颗)是白色。

100÷5=20(组)是黑色。

答：第77颗是白色，第68颗是白色，第100颗是黑色。

教学设计

简单的周期

教材第30~31页的内容。

1.在活动中探索并发现一些简单周期现象中的排列规律,能正确计算按照周期规律排列的物体或图形的数量。

2.在探索规律的过程中体会数学与日常生活的联系,获得成功的体验,增强学好数学的信心。

重点:探索并发现一些简单的周期现象中的排列规律。

难点:能在日常生活中运用简单的周期规律,计算或预见事物的发展。

课件。

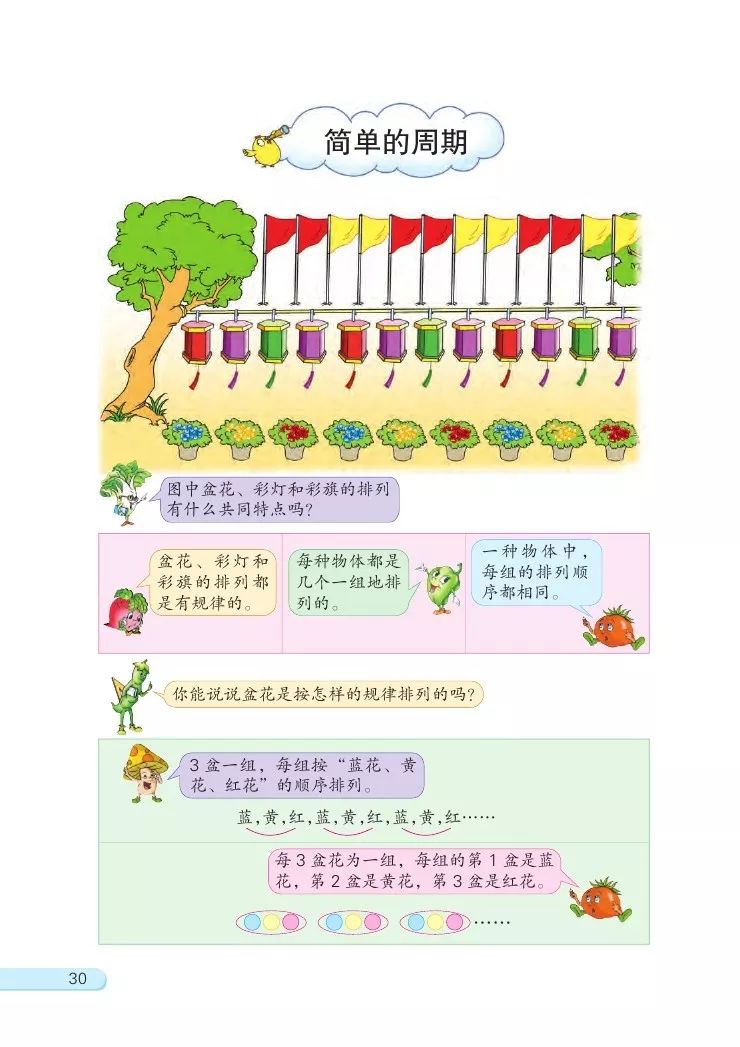
在重大的国庆节日期间,我们经常能见到各种摆放整齐的盆花。有的甚至能根据盆花的颜色,摆出各种不同的汉字。同学们想一想,为什么同样的盆花,能摆出这么多不同的字呢?

1.出示教材第30页情景图。

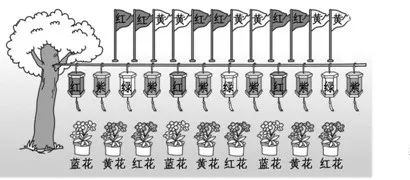
(1)图中盆花、彩灯和彩旗的排列有什么共同特点?

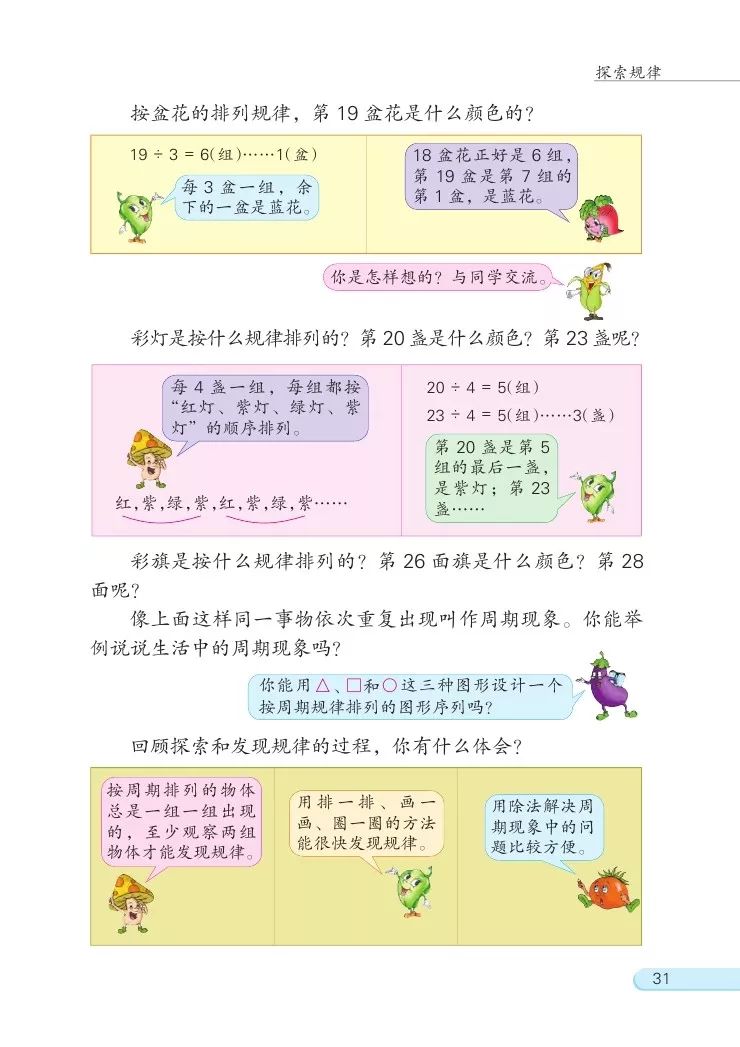
(2)你能说说盆花是按照怎样的规律排列的吗?按盆花的排列规律,第19盆花是什么颜色的?

(3)彩灯是按什么规律排列的?第20盏是什么颜色?第23盏呢?

 (4)彩旗是按什么规律排列的?第26面旗是什么颜色?第28面呢?

2.解读过程。

(1)通过观察发现,盆花、彩灯和彩旗的排列都是有规律的,每种物体都是从左边起,几个一组排列下来的,而且同种物体中,每组的排列顺序都相同。

(2)仔细观察盆花,是按照蓝、黄、红依次排列的,可以把每3盆看成一组,每组按“蓝花、黄花、红花”的顺序排列的,即每组的第1盆是蓝花,第2盆是黄花,第3盆是红花。可以像下面这样圈一圈:

像上面这样同一事物依次重复出现叫作周期现象。

盆花的排列可以看成每3盆是一个周期,要求第19盆是什么颜色的,就用19÷3=6(组)……1(盆),即19盆花中前面的18盆正好是6组,余下的1盆是第七组中的第1盆,也就是蓝花。

(3)按照上面的规律,可以发现彩灯是每4盏一组,每组都是按照“红灯、紫灯、绿灯、紫灯”的顺序排列的。

 20÷4=5(组),所以第20盏正好是第五组的最后一盏灯,也就是紫灯;

 23÷4=5(组)……3(盏),所以第23盏是第六组中的第3盏灯,也就是绿灯。

(4)通过观察可以发现,彩旗是按照“红红黄黄红红黄黄……”每4面旗子一个周期排列的。

26÷4=6(组)……2(面),第26面旗是第七组的第2面,应该是红旗;

28÷4=7(组),第28面旗正好是第七组的最后一面,应该是黄旗。

(5)拓展应用。

你能用△、□和○这三种图形设计一个按照周期规律排列的图形序列吗?

通过上面彩旗、彩灯和盆花的排列规律我们知道,按照周期排列的物体总是一组一组出现的,所以我们可以把△、□和○设计成任意排列的一组,比如按照“△、□、○”的顺序可以排成序列△、□、○、△、□、○、△、□、○……

还可以按照“△△、□□、○○”的顺序排成序列△△、□□、○○、△△、□□、○○……

不管怎样排列,按照周期排列的事物至少要观察两组才能发现它们的排列周期,进而可以通过计算得出周期序列中任一事物的规律。

3.课堂小结。

(1)同一种事物依次重复出现叫作周期现象。

(2)按照周期排列的物体至少要观察两组物体才能发现它们的排列周期。

小语

基础知识库

精彩呈现

免责声明：本文所有图文、音视频均来自网络，仅供学习交流使用，版权归原作者所有，除非无法确认，我们都会标明作者及出处，如有侵权烦请告知，我们会立即删除并表示歉意。谢谢！