Basic GMRES

最新推荐文章于 2024-09-29 08:52:28 发布

老李今天学习了吗

最新推荐文章于 2024-09-29 08:52:28 发布

阅读量5.4k

点赞数 3

分类专栏： PCG方法

本文链接：https://blog.csdn.net/weixin_29732003/article/details/106291605

版权

PCG方法专栏收录该内容

5 篇文章

订阅专栏

Basic GMRES

概述

GMRES意思为广义最小残差法，在求解稀疏矩阵上，是一个比较有效的方法。

我们要解决的问题依旧是一个方程组求解的问题 $A X = b$

这个算法可以理解为 $r_{0}$ 在 $Ar_{0}, A^{2}r_{0},...,A^{n-1})$ 这组基上的线性表示（可参考Krylov子空间的内容）

该算法参考的也是一个Arnoldi过程：
在这里插入图片描述
矩阵的结构为

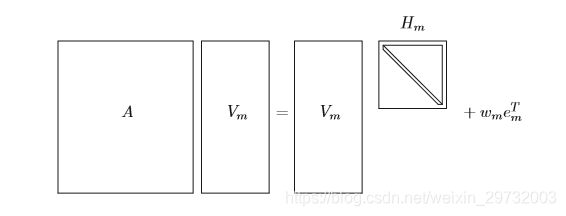
生成的 $H$ 也是一个上Hesenborg矩阵

我们通过如下的推导
在这里插入图片描述
可知，我们将一个求解稀疏矩阵方程组问题转化为了最小化上Hessenborg矩阵方程组的问题。

算法

在这里插入图片描述
最后关于系数 $y_{m}$ 怎么求，本文暂不考虑这个问题

matlab实现

%Basic GMRES
%Ax = b
function [V,R,H,res] = bGMRES(A,b,x0)
    %bGMRES:basic GMRES method
    %Input: x0:初值;A为mxm矩阵,b为解
    %Output: res为残差
    [m, ~] = size(A);
    R = Inf(m,m);omiga = zeros(m,m);%R为残差值，omiga为剩余向量
    H = zeros(m+1,m);V = zeros(m,m+1);%A*V=V*H
    %设定初值
    r0 = b-A*x0;
    V(:,1) = r0/norm(r0);
    for j = 1:m
        omiga(:,j) = A*V(:,j);
        for i = 1:j
            H(i,j) = omiga(:,j)'*V(:,i);
            omiga(:,j) = omiga(:,j) - H(i,j)*V(:,i);
        end
        H(j+1,j) = norm(omiga(:,j));
        R(:,j) = omiga(:,j);
        if abs(H(j+1,j)) < 1e-5
            sprintf('done')
            res = H(j+1,j);
            break;
        else
            V(:,j+1) = R(:,j)/H(j+1,j);
            res = H(j+1,j);
        end
    end
end

参考教材：《IterMethBook_2ndEd》