不等式的最大值_基本不等式求最值

最值在很多地方都会出现，并且出现即代表有一定难度，需要一定思考和计算。

如果能创造条件满足基本不等式成立的条件，那么就会很巧妙，就比较简单。一般会在这些地方考察用到基本不等式，选择题的中间部分，填空题倒数1-2个，解答题圆锥曲线第2问。

创造基本不等式成立条件：

一：都为正数；

二：和为定值或积为定值；

三：两数相等。

简称：一正，二定，三相等。

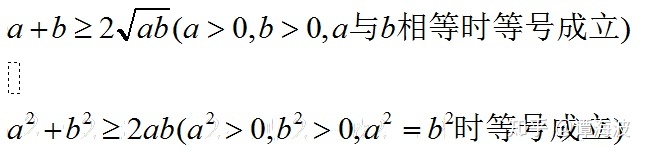
看着简单，但要创造满足的条件需要动脑筋，下面我们通过一道高考题来引导大家，怎么来创造基本不等式成立的条件。

拿到这道题，有同学就开始用基本不等式，想着那三个条件。x,y都大于0，x与2y和为定值,在这两个数相等时用基本不等式求出乘积最大值，进而求出分母最大值。但分子还不能求出，不能盲目这样做。

大家拿到题目时，不能一步基本不等式得到最值时，就不要想当然的认为满足了。这个时候大家可以先化简，进一步观察。

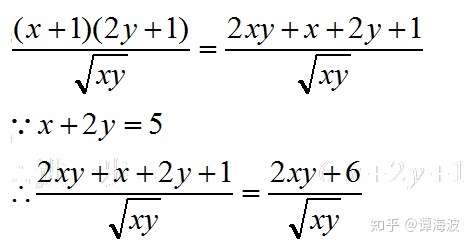
大家进一步想，要和取得最小值，说明乘积要一定，那我们就来创造乘积一定。

把我们这得到的这个式子拆分成两项。

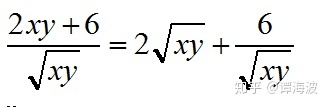
这个时候就明显了，两数相乘为定值，且根号xy也为正数，运用基本不等式得：

这是一道中等难度的利用基本不等式求最值，平时的模拟有很多比这个难。高考的难度和这个差不多。

我们再给一道训练，看大家掌握的怎么样。

中学数学有什么需要帮助的，可以关注我的公粽号“高中数学谭老师”，或者私信问我，我看见后都会回复，希望能帮助你，使你数学得到提升。