
数理化,不可怕,找对方法搞定它。关注我们免费获取更多学习干货、解题技巧、视频课程......
知识梳理 1. 基本不等式
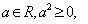
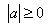
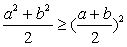 ,
,
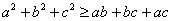 若a>b>0,m>0,则
若a>b>0,m>0,则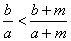 ;
若a,b同号且a>b,则
;
若a,b同号且a>b,则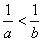 。
。
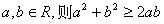 2. 均值不等式:
两个正数的均值不等式:
2. 均值不等式:
两个正数的均值不等式: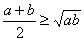 ,变形式:
,变形式: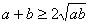 ,
,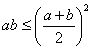 等。
3. 最值定理:设
等。
3. 最值定理:设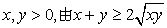 (1)如果x,y是正数,且积
(1)如果x,y是正数,且积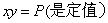 ,则x=y时,
,则x=y时,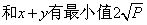 (2)如果x,y是正数,且和
(2)如果x,y是正数,且和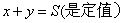 ,则x=y时,
,则x=y时, 运用最值定理求最值的三要素:一正二定三相等。
典型例题
知识点一:利用均值不等式求最值
例1:已知
运用最值定理求最值的三要素:一正二定三相等。
典型例题
知识点一:利用均值不等式求最值
例1:已知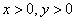 且满足
且满足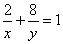 ,求
,求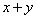 的最小值。
分析:利用
的最小值。
分析:利用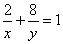 ,构造均值不等式。
利用基本不等式求最值要注意“一正二定三相等”即(1)要求各数均为正数;(2)要求“和”或“积”为定值;(3)要注意是否具备等号成立的条件。
解析:∵
,构造均值不等式。
利用基本不等式求最值要注意“一正二定三相等”即(1)要求各数均为正数;(2)要求“和”或“积”为定值;(3)要注意是否具备等号成立的条件。
解析:∵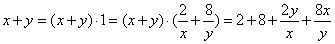 ,
,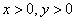 ,
∴
,
∴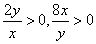 ,
,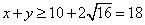 ,当且仅当
,当且仅当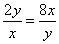 时等号成立,即
时等号成立,即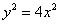 ,∴
,∴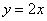 ,又
,又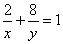 ,∴
,∴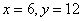 ∴当
∴当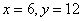 时,
时,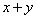 有最小值18。
例2:(1)已知0<x<
有最小值18。
例2:(1)已知0<x<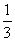 ,求函数y=x(1-3x)的最大值;
(2)求函数y=x+
,求函数y=x(1-3x)的最大值;
(2)求函数y=x+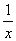 的值域。
分析:(1)由极值定理,可知需构造某个和为定值,可考虑把括号内外x的系数变成互为相反数;
(2)中,未指出x>0,因而不能直接使用基本不等式,需分x>0与x<0两种情况讨论。
利用基本不等式求积的最大值,关键是构造和为定值,为使基本不等式成立创造条件,同时要注意等号成立的条件是否具备。
解析:(1)解法一:
∵0<x<
的值域。
分析:(1)由极值定理,可知需构造某个和为定值,可考虑把括号内外x的系数变成互为相反数;
(2)中,未指出x>0,因而不能直接使用基本不等式,需分x>0与x<0两种情况讨论。
利用基本不等式求积的最大值,关键是构造和为定值,为使基本不等式成立创造条件,同时要注意等号成立的条件是否具备。
解析:(1)解法一:
∵0<x<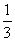 ,∴1-3x>0。
∴y=x(1-3x)=
,∴1-3x>0。
∴y=x(1-3x)=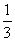 ·3x(1-3x)≤
·3x(1-3x)≤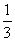 [
[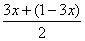 ]2=
]2=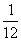 ,当且仅当3x=1-3x,即x=
,当且仅当3x=1-3x,即x=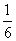 时,等号成立。
∴x=
时,等号成立。
∴x=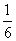 时,函数
时,函数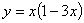 取得最大值
取得最大值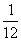 ,
解法二:
∵0<x<
,
解法二:
∵0<x<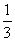 ,∴
,∴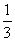 -x>0。
∴y=x(1-3x)=3x(
-x>0。
∴y=x(1-3x)=3x(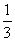 -x)≤3(
-x)≤3(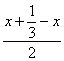 )2=
)2=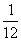 ,当且仅当x=
,当且仅当x=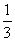 -x,即x=
-x,即x=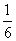 时,等号成立。
∴x=
时,等号成立。
∴x=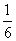 时,函数
时,函数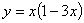 取得最大值
取得最大值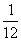 。
(2)解:
当x>0时,由基本不等式,得y=x+
。
(2)解:
当x>0时,由基本不等式,得y=x+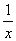 ≥2
≥2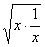 =2,当且仅当x=1时,等号成立。
当x<0时,y=x+
=2,当且仅当x=1时,等号成立。
当x<0时,y=x+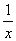 =-[(-x)+
=-[(-x)+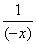 ]。
∵-x>0,∴(-x)+
]。
∵-x>0,∴(-x)+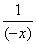 ≥2,当且仅当-x=
≥2,当且仅当-x=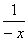 ,即x=-1时,等号成立。
∴y=x+
,即x=-1时,等号成立。
∴y=x+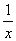 ≤-2。
综上,可知函数y=x+
≤-2。
综上,可知函数y=x+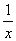 的值域为(-∞,-2]∪[2,+∞)。
知识点二:利用均值不等式证明
例3:已知
的值域为(-∞,-2]∪[2,+∞)。
知识点二:利用均值不等式证明
例3:已知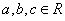 ,求证:
,求证: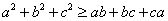 。
分析:因为是轮换对称不等式,可考虑由局部证整体。
综合法证明不等式常用两个正数的算术平均数不小于它们的几何平均数这一结论,运用时要结合题目条件,有时要适当变形。
解析:
。
分析:因为是轮换对称不等式,可考虑由局部证整体。
综合法证明不等式常用两个正数的算术平均数不小于它们的几何平均数这一结论,运用时要结合题目条件,有时要适当变形。
解析:
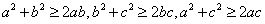 ,
相加整理得
,
相加整理得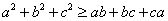 。
当且仅当
。
当且仅当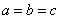 时等号成立。
例4:已知a,b为正数,求证:
时等号成立。
例4:已知a,b为正数,求证: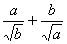 ≥
≥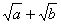 。
分析:观察式子结构,用基本不等式加以证明。
当要证明的不等式形式上比较复杂时,常通过分析法寻求证题思路。“分析法”与“综合法”是数学推理中常用的思维方法,特别是这两种方法的综合运用能力,对解决实际问题有重要的作用。这两种数学方法是高考考查的重要数学思维方法。
解析:解法1:∵a>0,b>0,
∴
。
分析:观察式子结构,用基本不等式加以证明。
当要证明的不等式形式上比较复杂时,常通过分析法寻求证题思路。“分析法”与“综合法”是数学推理中常用的思维方法,特别是这两种方法的综合运用能力,对解决实际问题有重要的作用。这两种数学方法是高考考查的重要数学思维方法。
解析:解法1:∵a>0,b>0,
∴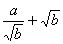 ≥
≥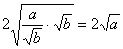 ,
,
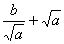 ≥
≥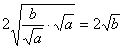 ,
两式相加,得
,
两式相加,得
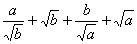 ≥
≥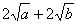 ,
∴
,
∴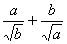 ≥
≥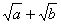 。
解法2:
。
解法2: ≥
≥
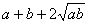
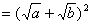 。
∴
。
∴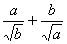 ≥
≥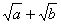 。
知识点三:均值不等式在实际中的应用
例5:某厂生产某种产品的年固定成本为250万元,每生产
。
知识点三:均值不等式在实际中的应用
例5:某厂生产某种产品的年固定成本为250万元,每生产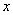 千件,需另投入成本为
千件,需另投入成本为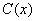 。当年产量不足80千件时,
。当年产量不足80千件时,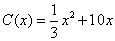 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,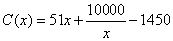 (万元)。每件商品售价为0.05万元。通过市场分析,该厂生产的商品能全部售完。
(1)写出年利润
(万元)。每件商品售价为0.05万元。通过市场分析,该厂生产的商品能全部售完。
(1)写出年利润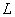 (万元)关于年产量
(万元)关于年产量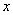 (千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
分析:凑出基本不等式的形式。
求形如
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
分析:凑出基本不等式的形式。
求形如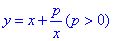 的函数的最值时可考虑用均值不等式,但要注意条件的限制,可借助函数的图象解题。
解析:
(
1
)当
的函数的最值时可考虑用均值不等式,但要注意条件的限制,可借助函数的图象解题。
解析:
(
1
)当
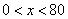 时,
时,
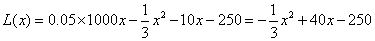 当
当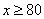 时,
时,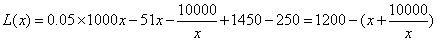 ∴
∴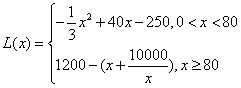 (2)当
(2)当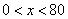 时,
时,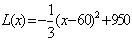 ,此时,当
,此时,当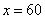 时,
时,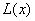 取得最大值
取得最大值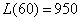 (万元);
当
(万元);
当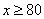 时,
时,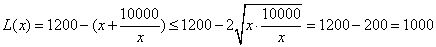 此时,当
此时,当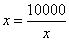 时,即
时,即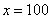 时,
时,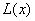 取得最大值1000万元。
所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元。
取得最大值1000万元。
所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元。








 本文介绍了如何运用均值不等式来解决高中数学中的最值问题,包括基本不等式、均值不等式、最值定理等概念,并通过多个例题详细解析了如何利用这些知识来求解函数的最大值和最小值。此外,还探讨了均值不等式在实际问题中的应用,如工厂利润最大化的计算。
本文介绍了如何运用均值不等式来解决高中数学中的最值问题,包括基本不等式、均值不等式、最值定理等概念,并通过多个例题详细解析了如何利用这些知识来求解函数的最大值和最小值。此外,还探讨了均值不等式在实际问题中的应用,如工厂利润最大化的计算。
















 4488
4488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








