<think>好的，我现在需要帮用户解决如何用Python编写计算三角形面积和周长的程序。用户已经提到了使用海伦公式，并且参考了站内的几个引用内容，我需要把这些信息整合起来，给出一个清晰的步骤和代码。
首先，用户的问题明确：输入三边长度，计算周长和面积，保留两位小数。同时，需要确保输入的三边能构成三角形，否则给出提示。根据引用中的内容，判断三角形是否有效的条件应该是任意两边之和大于第三边，但用户提供的引用[2]里的条件是a + b > c > a - b，这可能是一种简化的写法，可能只检查了一个边的情况，但实际上正确的条件应该是三个边都满足两边之和大于第三边。不过，用户提供的代码示例中使用了a + b > c > a - b，这可能是因为输入时已经固定了c的顺序？或者可能存在错误。需要指出正确的三角形判断条件。
接下来，我需要确保用户知道如何正确判断三角形是否有效。正确的条件应该是：任意两边之和大于第三边，即a + b > c，a + c > b，b + c > a。而用户提供的引用[2]中的条件可能不够全面，只检查了其中一个组合。因此，在编写代码时，应该检查所有三个条件，或者对输入的三边进行排序，使得c是最大的边，然后只需检查a + b > c。这样可以减少判断次数。例如，将三边排序后，最大的边放在最后，然后只需判断前两个边的和是否大于最大的边。
然后是计算周长和面积。周长就是三边之和，而面积使用海伦公式，即先计算半周长p，然后用sqrt(p*(p-a)*(p-b)*(p-c))。需要注意导入math模块，或者使用**0.5来计算平方根。根据用户的引用示例，他们使用了math.sqrt，所以代码中应该导入math。
此外，输出需要严格保留两位小数，可以使用Python的格式化字符串，例如"%.2f"或者format函数。在用户提供的引用[2]中，输出使用了%f，但用户的问题要求保留两位小数，所以需要调整格式说明符为%.2f。
现在，整合这些步骤：
1. 输入三个边的长度，可能需要转换为浮点数。
2. 判断这三个边是否能构成三角形。正确的方法是检查所有三个组合，或者将三边排序后检查最大的边是否小于另外两边之和。
3. 如果能构成，计算周长和面积，并保留两位小数输出。
4. 否则，输出不能构成三角形的提示。
可能的代码结构如下：
- 输入三个边a, b, c，转为float类型。
- 检查三角形有效性：将三个边排序，然后判断a + b > c（假设c是最大的）。
- 计算周长，半周长，然后面积。
- 格式化输出结果，保留两位小数。
同时，需要处理可能的输入错误，比如用户输入了非数字，但根据问题描述，测试用例保证数据有效，所以可能不需要处理异常。
现在，根据用户提供的引用[2]中的代码，他们的判断条件写的是a + b > c > a - b，这可能有问题，因为当c是最大的边时，应该只需要判断a + b > c，而其他边的情况已经由排序保证。但原代码中的条件是否正确呢？例如，c > a - b是否多余？比如，假设c是最大的边，那么a - b可能为负数，这时候c > a - b总是成立，所以条件可能等效于a + b > c。但为了准确，正确的条件应该是排序后判断最大的边是否小于另外两边之和。因此，在代码中，应该先将三边排序，然后判断最大的边是否小于其他两边之和。
所以，正确的步骤应该是：
输入三边a, b, c，然后转换为列表，排序，使得a, b, c按升序排列，这样c是最大的。然后判断a + b > c。如果是，则可以构成三角形。
这比检查所有三个条件更高效，因为排序后只需要检查一次。
因此，在代码中，可以这样做：
将输入的三个数存入列表，排序后赋值给a, b, c（升序），然后判断a + b > c。
例如：
sides = [a, b, c]
sides.sort()
a, b, c = sides
然后判断a + b > c。
如果这个条件满足，那么其他条件自动满足，因为c已经是最大的边，所以a + c > b 和 b + c > a 都成立，因为c >= b >= a，所以a + c >= a + b > c >= b，所以a + c > b成立，同理b + c > a也成立。因此，只需要判断a + b > c即可。
这样就能正确判断三角形是否有效。
然后计算周长，半周长，面积。
最后，格式化输出，保留两位小数。
现在，将这些步骤转化为代码：
首先输入三个边，转换为浮点数：
a = float(input("请输入第一条边长度："))
b = float(input("请输入第二条边长度："))
c = float(input("请输入第三条边长度："))
然后将三个边排序：
sides = [a, b, c]
sides.sort()
a_sorted, b_sorted, c_sorted = sides
判断a_sorted + b_sorted > c_sorted：
if a_sorted + b_sorted > c_sorted:
计算周长和面积
else:
输出不能构成三角形
计算周长：perimeter = a + b + c （注意这里应该用原始的a, b, c，还是排序后的？周长是三个边之和，不管顺序，所以可以用原始的或排序后的，结果一样）
但是，在排序后，a_sorted, b_sorted, c_sorted是排序后的，而原始的变量可能已经改变了，所以需要注意。例如，原来的a, b, c可能被重新赋值，因此可能需要用排序后的变量来计算周长，或者直接使用sum(sides)。或者，在排序前保存原始值？
例如：
original_a = a
original_b = b
original_c = c
或者，直接使用sum(sides)作为周长，因为排序后的三个数的和等于原来的三个数的和。
所以，周长可以计算为sum(sides) = a_sorted + b_sorted + c_sorted，等同于原始的三个数之和。
半周长p = sum(sides) / 2
面积则是math.sqrt(p*(p - a_sorted)*(p - b_sorted)*(p - c_sorted))
然后输出周长和面积，保留两位小数。
因此，完整的代码可能如下：
import math
a = float(input("请输入第一条边长度："))
b = float(input("请输入第二条边长度："))
c = float(input("请输入第三条边长度："))
# 将三边排序
sides = [a, b, c]
sides.sort()
a_sorted, b_sorted, c_sorted = sides
if a_sorted + b_sorted > c_sorted:
perimeter = a + b + c # 或者使用sum([a, b, c])
p = perimeter / 2
area = math.sqrt(p * (p - a) * (p - b) * (p - c)) # 这里可能需要用排序后的边吗？
# 不，海伦公式中参数的顺序无关，因为乘法是交换的，所以用原始边或排序后的边都可以
print(f"周长：{perimeter:.2f}")
print(f"面积：{area:.2f}")
else:
print("无法构成三角形")
不过，这里有一个问题：在计算面积时，p*(p - a)*(p - b)*(p - c)中的a, b, c是否是排序后的？因为如果用户输入的边没有按顺序，比如c不是最大的，那么p - c可能是负数，导致平方根出错。但根据之前的判断，我们已经确定三边可以构成三角形，所以p - a, p - b, p - c都应该为正数吗？或者是否应该使用排序后的边来计算？
实际上，海伦公式中的p是半周长，而每个(p - a), (p - b), (p - c)都必须为正数，否则乘积为负，无法计算平方根。所以在判断三角形有效后，这三个项都应该是正数。因此，不管是否排序，只要三角形有效，海伦公式中的乘积就会是非负的，所以可以安全地计算平方根。因此，在代码中，可以使用原始输入的a, b, c来计算面积，因为无论如何，只要通过三角形判断，这些值都是有效的。
但为了保险起见，或许应该使用排序后的边，因为已经确保了c_sorted是最大的边，这样在计算p - c_sorted时，可能出现负数吗？例如，当三边是3,4,5，排序后是3,4,5，p = (3+4+5)/2=6，p -5=1>0。因此，在判断条件a_sorted + b_sorted > c_sorted的情况下，c_sorted < a_sorted + b_sorted，而根据三角形不等式，每个边都小于另外两边之和，因此每个边都小于半周长，所以p - a, p - b, p - c 都是正数。所以，无论使用原始边还是排序后的边，结果都是正确的。因此，在计算面积时，可以使用原始的a, b, c。
但用户提供的引用[2]中的代码并没有排序，而是直接使用输入的a, b, c，并且判断条件为a + b > c > a - b。这可能存在问题，因为当c不是最大的边时，这个条件可能无法正确判断。例如，假设输入的边是5, 1, 2，那么最大的边是5，但是原代码中的条件可能判断错误，因为a=5, b=1, c=2，此时a + b =6 > c=2，但显然这三个边无法构成三角形，因为1 + 2 =3 <5。所以，原代码中的判断条件可能不正确，因为未排序的情况下，直接判断a + b > c可能当c不是最大的边时，导致错误的判断。因此，正确的做法是先将三边排序，然后判断最大的边是否小于其他两边之和。
因此，在用户提供的引用[2]中的代码可能存在错误，所以在我的回答中需要正确判断三角形有效性，即通过排序后检查最大的边是否小于另外两边之和。
因此，正确的判断条件应该是在排序后检查a_sorted + b_sorted > c_sorted。
因此，在代码中，排序是必要的步骤，以确保最大的边是c_sorted。
现在，回到代码部分，正确的判断条件已经处理，那么计算面积时是否可以使用原始输入的a, b, c？
是的，因为无论顺序如何，海伦公式的结果都是相同的，因为乘法是交换的。例如，p*(p - a)*(p - b)*(p - c)不管a, b, c的顺序如何，结果都是一样的。因此，使用原始输入的a, b, c进行计算是正确的。
因此，代码中的面积计算可以写成：
p = (a + b + c) / 2
area = math.sqrt(p * (p - a) * (p - b) * (p - c))
这样更直观，因为用户输入的是a, b, c，而不是排序后的值。
因此，综合起来，正确的代码应该是：
import math
a = float(input("请输入第一条边长度a: "))
b = float(input("请输入第二条边长度b: "))
c = float(input("请输入第三条边长度c: "))
# 判断能否构成三角形
sides = [a, b, c]
sides.sort()
a_sorted, b_sorted, c_sorted = sides # 排序后c_sorted是最大的边
if a_sorted + b_sorted > c_sorted:
perimeter = a + b + c
p = perimeter / 2
area = math.sqrt(p * (p - a) * (p - b) * (p - c))
print(f"周长：{perimeter:.2f}")
print(f"面积：{area:.2f}")
else:
print("不能构成三角形")
这样就能正确判断并计算了。
现在，关于格式化输出，用户要求严格保留两位小数。在Python中，可以使用format函数或者f-string，如上面的代码示例所示，使用:.2f来格式化。
总结步骤：
1. 输入三条边并转为浮点数。
2. 将边排序，确保最大的边在最后。
3. 判断前两条边的和是否大于最大的边。
4. 如果是，计算周长和面积，否则提示无法构成。
5. 输出结果保留两位小数。
此外，用户提供的引用[2]中的判断条件可能存在问题，所以需要纠正这一点，确保使用排序后的边来正确判断。
最后，测试一下代码是否正确。例如，输入3,4,5，周长应为12，面积6。代码输出应为周长12.00，面积6.00。再比如，输入2,2,3，判断条件成立，周长7.00，面积用海伦公式计算正确。如果输入1,2,3，排序后为1,2,3，1+2=3不大于3，所以无法构成三角形。
现在，用户的问题已经解决，接下来需要生成相关问题，根据系统指令的第六点，生成相关问题。
相关问题可能涉及如何优化判断条件，如何处理非数字输入，或者海伦公式的其他应用，以及三角形的其他性质等。</think>### Python计算三角形面积和周长的实现步骤
1. **输入处理**
通过`input()`函数获取三条边长度，并转换为浮点型：
```python
a = float(input("请输入第一条边长度a: "))
b = float(input("请输入第二条边长度b: "))
c = float(input("请输入第三条边长度c: "))
```
2. **三角形有效性验证**
将三边排序后验证是否满足三角形不等式定理[^2]：
```python
sides = [a, b, c]
sides.sort()
a_sorted, b_sorted, c_sorted = sides
if a_sorted + b_sorted > c_sorted:
# 计算周长和面积
else:
print("不能构成三角形")
```
3. **周长与面积计算**
- 周长公式：$C = a + b + c$
- 海伦公式：
$$ p = \frac{a+b+c}{2}, \quad S = \sqrt{p(p-a)(p-b)(p-c)} $$
代码实现：
```python
perimeter = a + b + c
p = perimeter / 2
area = math.sqrt(p * (p - a) * (p - b) * (p - c))
```
4. **格式化输出**
使用`f-string`保留两位小数：
```python
print(f"周长：{perimeter:.2f}")
print(f"面积：{area:.2f}")
```
### 完整代码
```python
import math
a = float(input("请输入第一条边长度a: "))
b = float(input("请输入第二条边长度b: "))
c = float(input("请输入第三条边长度c: "))
sides = [a, b, c]
sides.sort()
a_sorted, b_sorted, c_sorted = sides
if a_sorted + b_sorted > c_sorted:
perimeter = a + b + c
p = perimeter / 2
area = math.sqrt(p * (p - a) * (p - b) * (p - c))
print(f"周长：{perimeter:.2f}")
print(f"面积：{area:.2f}")
else:
print("不能构成三角形")
```
### 注意事项
- 输入需为有效数字，且能构成三角形（测试用例已保证）[^3]。
- 海伦公式要求三边满足三角形不等式，否则平方根内可能出现负数。
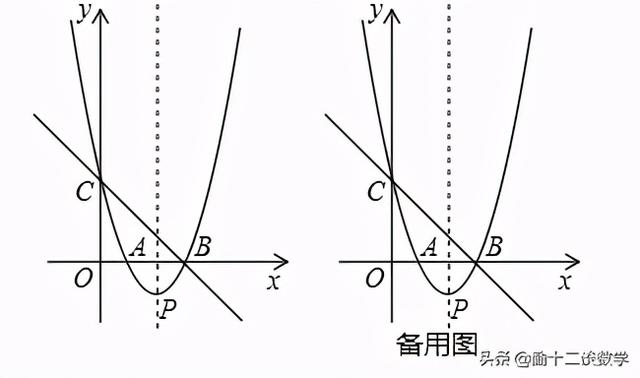
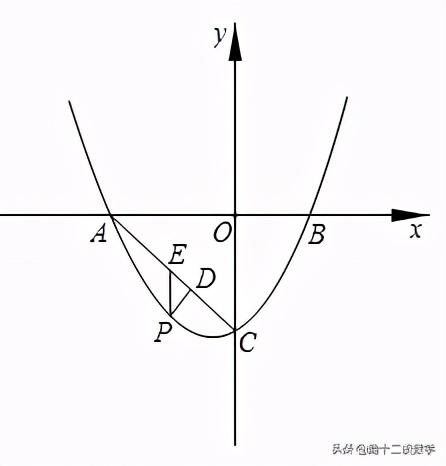
博客聚焦二次函数中三角形周长的最值问题，介绍两种解题方法。一是将军饮马模型，通过抛物线对称性和三点共线求周长最小值；二是利用相似三角形或锐角三角函数，将周长转化为线段长度，用设点法求最值。
扫一扫
1641
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
