三角形周长最短问题_初中数学最短路径问题总结

最新推荐文章于 2024-02-03 10:24:47 发布

Ben Franklin

最新推荐文章于 2024-02-03 10:24:47 发布

阅读量8.2k

点赞数 2

文章标签：三角形周长最短问题

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_35101659/article/details/112467195

版权

本文总结了初中数学中的12个最短路径问题，涉及直线上的点、对称性、三角形周长和费马点。通过构造和几何性质，找出使路径、周长或距离之和最小或最大的点的位置，包括将军饮马问题、造桥选址问题和费马点的构造与证明。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、十二个基本问题概述

问题一：在直线 l 上求一点 P，使得 PA + PB 值最小 .

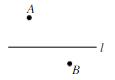
作法：连接 AB，与直线 l 的交点即为 P 点 .

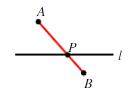
原理：两点之间线段最短 . PA + PB 最小值为 AB .

问题二：(“将军饮马问题”)在直线 l 上求一点 P，使得 PA + PB 值最小 .

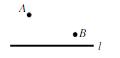
作法：作点 B 关于直线 l 的对称点 B＇，连接 AB' 与 l 的交点即为点 P．

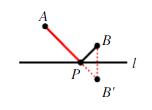
原理：两点之间线段最短． PA + PB 最小值为 AB' .

问题三：在直线 l1、l2 上分别求点 M、N，使得 △PMN 的周长最小．

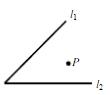
作法：分别作点 P 关于两条直线的对称点 P' 和 P''，连接 P'P''，与两条直线的交点即为点 M，N．

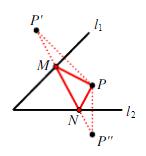
原理：两点之间线段最短． PM + MN + PN 的最小值为线段 P'P'' 的长．</

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。