ROC 曲线/准确率、覆盖率（召回）、命中率、Specificity（负例的覆盖率）

 

欢迎关注博主主页，学习python视频资源

sklearn实战-乳腺癌细胞数据挖掘（博主亲自录制视频教程）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

 

 统计项目联系QQ：231469242

 

 用条件概率理解混合矩阵容易得多

sensitivity：真阳性条件下，测试也是阳性

specificity:真阴性条件下，测试也是阴性

FALSE positive:真阴性条件下，测试却是阳性

FALSE negative：真阳性条件下，测试却是阴性

 

混淆矩阵图谱

 

 

Excel绘制ROC

 

 

 

 

 

 

 

 

 

 

 

 

准确度 (ACC, accuracy)ACC = (TP + TN) / (P + N)即：(真阳性+真阴性) / 总样本数

敏感性sensitivity=召回率recall

精准率precision=阳性预测率

 

 敏感性和假阳性率呈现正比例

敏感性和准确性（阳性预测率）呈现反比例

ROC和PRC曲线说明：敏感性（召回率）不是越高越好，敏感性太高，假阳性率也会上升。（会损失掉一些好客户）

敏感性太高，阳性预测率（准确率）会下降。（机器学习改善）

 

 

 

2.2 P-R曲线

在P-R曲线中，Precision为横坐标，Recall为纵坐标。在ROC曲线中曲线越凸向左上角约好，在P-R曲线中，曲线越凸向右上角越好。P-R曲线判断模型的好坏要根据具体情况具体分析，有的项目要求召回率较高、有的项目要求精确率较高。P-R曲线的绘制跟ROC曲线的绘制是一样的，在不同的阈值下得到不同的Precision、Recall，得到一系列的点，将它们在P-R图中绘制出来，并依次连接起来就得到了P-R图。两个分类器模型（算法）P-R曲线比较的一个例子如下图所示：

作者：金戈戈
链接：https://www.zhihu.com/question/30643044/answer/48955833
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

再说PRC， precision recall curve。和ROC一样，先看平滑不平滑（蓝线明显好些），在看谁上谁下（同一测试集上），一般来说，上面的比下面的好（绿线比红线好）。F1（计算公式略）当P和R接近就也越大，一般会画连接(0,0)和(1,1)的线，线和PRC重合的地方的F1是这条线最大的F1（光滑的情况下），此时的F1对于PRC就好象AUC对于ROC一样。 一个数字比一条线更方便调模型。
<img src="https://pic4.zhimg.com/50/3378a75e33245f6e0aac33717b19512c_hd.jpg" data-rawwidth="800" data-rawheight="600" class="origin_image zh-lightbox-thumb" width="800" data-original="https://pic4.zhimg.com/3378a75e33245f6e0aac33717b19512c_r.jpg"> 以上两个指标用来 判断模型好坏，图有些不恰当。。。但是有时候模型没有单纯的谁比谁好（比如图二的蓝线和青线），那么选择模型还是要结合具体的使用场景。

 

下面是两个场景：
1. 地震的预测
对于地震的预测，我们希望的是RECALL非常高，也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲PRECISION。情愿发出1000次警报，把10次地震都预测正确了；也不要预测100次对了8次漏了两次。
2. 嫌疑人定罪
基于不错怪一个好人的原则，对于嫌疑人的定罪我们希望是非常准确的。及时有时候放过了一些罪犯（recall低），但也是值得的。

对于分类器来说，本质上是给一个概率，此时，我们再选择一个CUTOFF点（阀值），高于这个点的判正，低于的判负。那么这个点的选择就需要结合你的具体场景去选择。反过来，场景会决定训练模型时的标准，比如第一个场景中，我们就只看RECALL=99.9999%（地震全中）时的PRECISION，其他指标就变得没有了意义。

如果只能选一个指标的话，肯定是选PRC了。可以把一个模型看的一清二楚。

 

作者：金戈戈
链接：https://www.zhihu.com/question/30643044/answer/48955833
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

再说PRC， precision recall curve。和ROC一样，先看平滑不平滑（蓝线明显好些），在看谁上谁下（同一测试集上），一般来说，上面的比下面的好（绿线比红线好）。F1（计算公式略）当P和R接近就也越大，一般会画连接(0,0)和(1,1)的线，线和PRC重合的地方的F1是这条线最大的F1（光滑的情况下），此时的F1对于PRC就好象AUC对于ROC一样。 一个数字比一条线更方便调模型。
<img src="https://pic4.zhimg.com/50/3378a75e33245f6e0aac33717b19512c_hd.jpg" data-rawwidth="800" data-rawheight="600" class="origin_image zh-lightbox-thumb" width="800" data-original="https://pic4.zhimg.com/3378a75e33245f6e0aac33717b19512c_r.jpg"> 以上两个指标用来 判断模型好坏，图有些不恰当。。。但是有时候模型没有单纯的谁比谁好（比如图二的蓝线和青线），那么选择模型还是要结合具体的使用场景。

 

下面是两个场景：
1. 地震的预测
对于地震的预测，我们希望的是RECALL非常高，也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲PRECISION。情愿发出1000次警报，把10次地震都预测正确了；也不要预测100次对了8次漏了两次。
2. 嫌疑人定罪
基于不错怪一个好人的原则，对于嫌疑人的定罪我们希望是非常准确的。及时有时候放过了一些罪犯（recall低），但也是值得的。

对于分类器来说，本质上是给一个概率，此时，我们再选择一个CUTOFF点（阀值），高于这个点的判正，低于的判负。那么这个点的选择就需要结合你的具体场景去选择。反过来，场景会决定训练模型时的标准，比如第一个场景中，我们就只看RECALL=99.9999%（地震全中）时的PRECISION，其他指标就变得没有了意义。

如果只能选一个指标的话，肯定是选PRC了。可以把一个模型看的一清二楚。

 

 

 

左上角：模型很好预测

中间红线是随机线，0.5/0.5概率，无法分类

 

 

 

X轴为False Positive （1-specificity）

y轴为True Positive(sensitivity)

 

宁可误杀一千不可放走一人，只要全部认定为阳性，敏感度就是百分之百，但说明调高敏感度同时，假阳性概率也会随之提高

当全部认定为阳性，阴性数量为0，specificity=0,  假阳性1-specificity=1，假阳性也是最高。

 

TP(sensitive)提高，FP（false positive）也增高，当拐点达到左上角时，达到最佳值，

 

 

 

 

 True positive rate=red pixal to the right of line /all red pixal

 

 false positive rate=blue pixal to the right of line/all blue pixal

 

sensitivity=黑色竖线右边红色像素面积/红色像素总面积
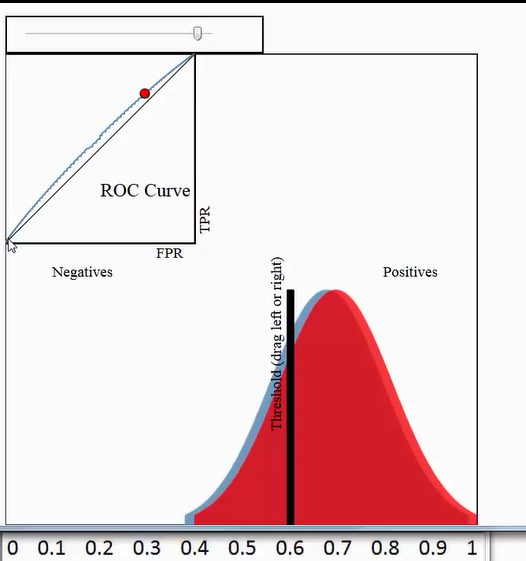
false positive=黑色竖线右边绿色像素面积/蓝色像素总面积

 

 

曲线面积为1是最理想状态，

 

 

 

曲线面积0.8，表示0.8的概率随机事件阳性概率大于阴性

 

 

 

 

 

 

 

蓝色表示不接受

红色表示接受

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

这种roc很难区别分类

 

 

 

最早用于英国雷达分辨鸟或德国飞机的概率

 

 

7.4 Receiver-Operating-Characteristic (ROC) Curve
Closely related to sensitivity and specificity is the Receiver-Operating-
Characteristic (ROC) curve. This is a graph displaying the relationship between the
true positive rate (on the vertical axis) and the false positive rate (on the horizontal

axis). The technique comes from the field of engineering, where it was developed to
find the predictor which best discriminates between two given distributions: ROC
curves were first used duringWWII to analyze radar effectiveness. In the early days
of radar, it was sometimes hard to tell a bird from a plane. The British pioneered
using ROC curves to optimize the way that they relied on radar for discriminating
between incoming German planes and birds.
Take the case that we have two different distributions, for example one from
the radar signal of birds and one from the radar signal of German planes, and
we have to determine a cut-off value for an indicator in order to assign a test
result to distribution one (“bird”) or to distribution two (“German plane”). The only
parameter that we can change is the cut-off value, and the question arises: is there
an optimal choice for this cut-off value?
The answer is yes: it is the point on the ROC-curve with the largest distance to
the diagonal (arrow in Fig.7.10).3
Fig.

 

 

 

 

 

受试者工作特征曲线 （receiver operating characteristic curve，简称ROC曲线），又称为 感受性曲线（sensitivity curve）。得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一 信号刺激的反应，只不过是在几种不同的判定标准下所得的结果而已。接受者操作特性曲线就是以假阳性概率（False positive rate）为 横轴，击中概率为纵轴所组成的坐标图，和被试在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。

ROC 曲线是根据一系列不同的二分类方式（分界值或决定阈），以真阳性率（灵敏度）为纵坐标，假阳性率（1-特异度）为横坐标绘制的曲线。传统的诊断试验评价方 法有一个共同的特点，必须将试验结果分为两类，再进行统计分析。ROC曲线的评价方法与传统的评价方法不同，无须此限制，而是根据实际情况，允许有中间状 态，可以把试验结果划分为多个有序分类，如正常、大致正常、可疑、大致异常和异常五个等级再进行统计分析。因此，ROC曲线评价方法适用的范围更为广泛。

 

 

主要作用

编辑

1.ROC曲线能很容易地查出任意界限值时的对疾病的识别能力。

2.选择最佳的诊断界限值。ROC曲线越靠近左上角,试验的 准确性就越高。最靠近左上角的ROC曲线的点是错误最少的最好 阈值，其假阳性和假阴性的总数最少。

3.两种或两种以上不同诊断试验对疾病识别能力的比较。在对同一种疾病的两种或两种以上诊断方法进行比较时，可将各试验的ROC曲线绘制到同一坐标中，以直观地鉴别优劣，靠近左上角的ROC曲线所代表的受试者工作最准确。亦可通过分别 计算各个试验的ROC曲线下的面积(AUC)进行比较，哪一种试验的 AUC最大，则哪一种试验的诊断价值最佳。

 

 

1.ROC曲线绘制。依据专业知识，对疾病组和参照组测定结果进行分析，确定测定值的上下限、 组距以及截断点（cut-off point），按选择的组距间隔列出累积 频数分布表，分别计算出所有截断点的敏感性、 特异性和假阳性率（1-特异性）。以 敏感性为纵坐标代表 真阳性率，（1-特异性）为横坐标代表 假阳性率，作图绘成ROC曲线。

2.ROC曲线评价 统计量计 算。ROC曲线下的面积值在1.0和0.5之间。在AUC>0.5的情况下，AUC越接近于1，说明诊断效果越好。AUC在 0.5～0.7时有较低准确性，AUC在0.7～0.9时有一定准确性，AUC在0.9以上时有较高准确性。AUC=0.5时，说明诊断方法完全不起作 用，无诊断价值。AUC<0.5不符合真实情况，在实际中极少出现。

3.两种诊断方法的统计学比较。两种诊断方法的比较时，根据不同的试验设计可采用以下两种方法：①当两种诊断方法分别在不同受试者身上进行时，采用成组 比较法。②如果两种诊断方法在同一受试者身上进行时，采用配对比较法

 

 

 

　 ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系，它通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和 特异性，再以敏感性为纵坐标、（1-特异性）为横坐标绘制成曲线，曲线下面积越大，诊断准确性越高。在ROC曲线上，最靠近坐标图左上方的点为敏感性和特 异性均较高的临界值。

 

 

ROC曲线的例子

　 　考虑一个二分问题，即将实例分成正类（positive）或负类（negative）。对一个二分问题来说，会出现四种情况。如果一个实例是正类并且也 被 预测成正类，即为真正类（True positive）,如果实例是负类被预测成正类，称之为假正类（False positive）。相应地，如果实例是负类被预测成负类，称之为真负类（True negative）,正类被预测成负类则为假负类（false negative）。

FN：漏报，没有正确找到的匹配的数目；

TN：正确拒绝的非匹配对数；

　　列联表如下表所示，1代表正类，0代表负类。　　

		预测
		1	0	合计
实际	1	True Positive（TP）	False Negative（FN）	Actual Positive(TP+FN)
	0	False Positive（FP)	True Negative(TN)	Actual Negative(FP+TN)
合计		Predicted Positive(TP+FP)	Predicted Negative(FN+TN)	TP+FP+FN+TN

从列联表引入两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为TPR=TP/ (TP+ FN)，刻画的是分类器所识别出的 正实例占所有正实例的比例。另外一个是假正类率(false positive rate, FPR),计算公式为FPR= FP / (FP + TN)，计算的是分类器错认为正类的负实例占所有负实例的比例。还有一个真负类率（True Negative Rate，TNR），也称为specificity,计算公式为TNR=TN/ (FP+ TN) = 1-FPR。

其中，两列True matches和True non-match分别代表两行Pred matches和Pred non-match分别代表匹配上和预测匹配上的

 

FPR = FP/(FP + TN) 负样本中的错判率（假警报率）

TPR = TP/(TP + TN) 判对样本中的正样本率（命中率）

ACC = (TP + TN) / P+N 判对准确率

 

　 　在一个二分类模型中，对于所得到的连续结果，假设已确定一个阀值，比如说 0.6，大于这个值的实例划归为正类，小于这个值则划到负类中。如果减小阀值，减到0.5，固然能识别出更多的正类，也就是提高了识别出的正例占所有正例 的比类，即TPR,但同时也将更多的负实例当作了正实例，即提高了FPR。为了形象化这一变化，在此引入ROC，

ROC曲线和它相关的比率

(a)理想情况下，TPR应该接近1，FPR应该接近0。

ROC曲线上的每一个点对应于一个threshold，比如Threshold最大时，TP=FP=0，对应于原点；Threshold最小时，TN=FN=0，对应于右上角的点(1,1)

(b)随着阈值theta增加，TP和FP都减小，TPR和FPR也减小，ROC点向左下移动；

 

　 　Receiver Operating Characteristic,翻译为"接受者操作特性曲线"，够拗口的。曲线由两个变量1-specificity 和 Sensitivity绘制. 1-specificity=FPR，即假正类率。Sensitivity即是真正类率，TPR(True positive rate),反映了正类覆盖程度。这个组合以1-specificity对sensitivity,即是以代价(costs)对收益 (benefits)。

       此外，ROC曲线还可以用来计算“均值平均精度”（　　下表是一个逻辑回归得到的结果。将得到的实数值按大到小划分成10个个数 相同的部分。　　

Percentile	实例数	正例数	1-特异度(%)	敏感度(%)
10	6180	4879	2.73	34.64
20	6180	2804	9.80	54.55
30	6180	2165	18.22	69.92
40	6180	1506	28.01	80.62
50	6180	987	38.90	87.62
60	6180	529	50.74	91.38
70	6180	365	62.93	93.97
80	6180	294	75.26	96.06
90	6180	297	87.59	98.17
100	6177	258	100.00	100.00