板式橡胶支座弹性模量怎样计算_连载桥梁微技术37【橡胶支座的刚度模拟1】

橡胶支座的刚度模拟-1

midas Civil

midas Civil是桥梁领域通用结构分析及设计系统，它具有直观的操作界面，并且采用了尖端的计算机显示技术。midas Civil集成了静力分析、动力分析、几何非线性分析、屈曲分析、移动荷载分析、PSC桥分析、悬索桥分析、水化热分析等分析设计功能。

具体问题：

对于广大用户一直关心的如何在程序中模拟橡胶支座的刚度问题，下面给出详细的解释说明。

解决方法：

1) 普通板式橡胶支座介绍

图 1.1板式橡胶支座

①特点：性能优良、构造简单、价格低、无需维护、易更换、缓冲隔震、建筑高度低等特点。

②构造：由多层橡胶片与薄钢板硫化、粘合而成，它有足够的竖向钢度，能将上部构造的反力可靠的传递给墩台；有良好的弹性，以适应梁端的转动；又有较大的剪切变形能力，以满足上部构造的水平位移。

③活动机理：利用橡胶支座的不均匀弹性压缩实现转角，利用剪切变形实现水平位移。

④适用范围：

i.普通板式橡胶支座适用于跨度小于 30m、位移量较小的桥梁；正交桥梁用矩形支座；曲线桥、斜交桥及圆柱墩桥用圆形支座。

ii.四氟板式橡胶支座适用于大跨度、多跨连续、简支梁连续板等结构的大位移量桥梁。它还可用作连续梁顶推及 T 型梁横移中的滑块。矩形、圆形四氟板式橡胶支座的应用分别与矩形、圆形普通板式橡胶支座相同。

2)规范中的相关规定

①按结构型式分为：

i.普通板式橡胶支座分为矩形板式橡胶支座(代号 GJZ)、圆形板式橡胶支座(代号 GYZ)；

ii.四氟滑板式橡胶支座分为矩形四氟滑板橡胶支座(代号 GJZF4)、圆形四氟滑板橡胶支座(代号 GYZF4)

②按支座材料和适用温度分为：

1)常温型橡胶支座应采用氯丁橡胶(CR)生产，适用温度为：-25°C  ～ 60°C  。 

2)耐寒型橡胶支座应采用天然橡胶(NR)生产，适用温度为：-40°C  ～ 60°C  。 

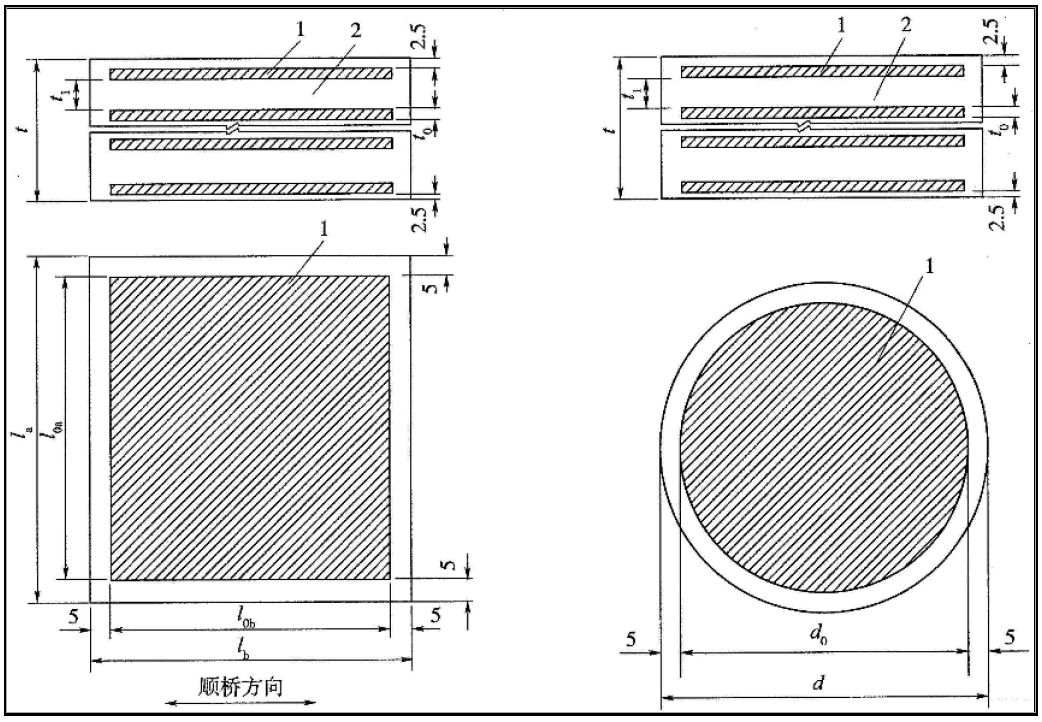
图 1.2       橡胶支座布置图 

3) Civil 中的模拟方式

使用“边界条件”→“弹性连接”，模拟支座的 6 个刚度。(如图 1.3、1.4 所示)

以材料力学角度理解： 

沿单元局部坐标系 x 轴方向刚度：SDx=EA/L

沿单元局部坐标系 y、z 轴方向刚度：SDy=SDz=GA/L

绕单元局部坐标系 x 轴方向转动刚度：SRx=GIp/L

绕单元局部坐标系 y、z 轴方向转动刚度：SRy=EIy/L、SRz=EIz/L， 

(式中：E-弹性模量；G-切变模量；A-面积；L-支座高度(厚度)；Iy、Iz-

截面抗弯惯性矩；Ip-截面抗扭惯性矩。) 

注：由于在这里输入的各向刚度的单位是线刚度，所以在模拟支座顶、底两个节点的间距时，其间距值可以是实际的支座高度，也可以是为了模型查看方便，设置一个稍大些的值，都不影响分析结果。 

图 1.3    弹性连接的定义 

图 1.4     模型中的“弹性连接” 

4) 结合规范(JT/T 4-2004)和(JTG D62-2004)举例说明支座刚度的计算方法

例：我们分别选取矩形支座和圆形支座来计算(实际设计时，支座的选取要根据支反力及 D62 规范来确定)

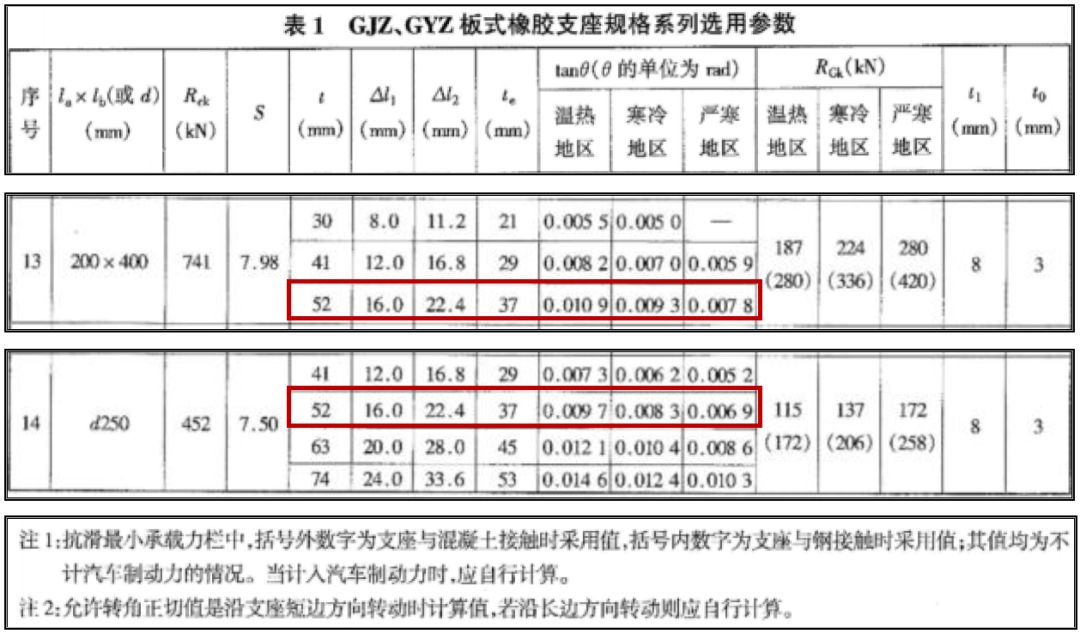
图 1.5     板式橡胶支座规格表 

① SDx 的计算(即支座的抗压刚度计算)

图 1.6      规范中的相关计算公式 

矩形支座：La×Lb-200×400/52：S=7.98

(注：S 在支座选用表中可直接查到，在此主要是说明计算过程，参见 D62，8.4.1) 

支座剪变模量 Ge 的计算 

本例按常温选取，Ge=1MPa(参见 D62，8.4.1) 

(注：Ge 选取的值是根据试验得到，同时，试验规定 Ge 的测定是在平均压应力σc =10MPa作用下得到的，也就是说是在承压状态下得到的剪变模量，也就支座不存在刚度计算时，是否在承压状态下计算的刚度这个问题了。 

支座抗压弹性模量 Ee 计算 

圆形支座：Ee = 5.4Ge S2 = 5.4 × 1 × 7.52 = 303.75MPa

② SDy、SDz 的计算(即支座的剪切刚度计算)

材料力学的角度计算公式：SDy=SDz=GA/L，结合规范后的计算方式如下： 

i.G 的计算(G=Ge=1MPa 参见 D62，8.4.1)

ii.A 的计算(A=kAe，计算见前页 Ae 计算，圆形 k=0.9,矩形 k=5/6，参见帮助文档-截面-剪切面积部分)

iii.L 的计算(L=te，计算过程略，参见 SDx 中的 te 计算)

综上，midas Civil 中弹性连接沿局部坐标 y、z 轴方向刚度 SDy=SDz

③ SRx 的计算(即支座的抗扭刚度计算)

材料力学的角度计算公式：SRx=GIp/L，结合规范后的计算方式如下： 

i. Ip 的计算(支座截面的抗扭刚度)

抗扭刚度 Ip 是抵抗扭矩的刚度。它不同于为了计算扭矩作用下的截面剪应力所使用的极惯性矩。但是，当截面形状是圆形或厚板圆环时，其抗扭刚度与极惯性矩相同。

在 midas Civil 的帮助文件中，给出了常见截面 Ip 的计算公式，如图 1.7 所以：