凸优化 & 1概念

---恢复内容开始---

放射集合
系数之和为1 相加仍然能在集合内，就是 纺射集合
子空间加一个常熟 就是纺射集合 ，
例题2.1
一类特殊的线性方程组的解可以看作纺射 集合

纺射包 aff C
是由集合C中所有店组成的仿射组合

定义集合C的维度为其纺射包的位数，

特例 ： R2上的单位元 纺射包 是全空间R 维度为2 但是一般来说 单位元还的维度是1

如果以一个集合 C的仿设纬度小于n
称 集合C的相对内部为aff C的内部
记为relint

例题2.2
考虑 R3中的处于(x1,x2）平面的一个正方形

C= 一个上述正方形
其纺射包是一个平面，但是内部为空，相对内部不为空

C的边界是自身，但是相对边界是其边框（相对边界对应相对内部）

2.1.4 凸集

集合C被称为凸集，当C中元素 加和为1（但都为正数时）还在 C集内 称为凸集

集合C中所有点的凸组合称为凸包
记为conv C

凸组合的概念可以扩展到无线级数，积分和大多数形式的概况v分布

级数扩展：
无穷级数系数之和为1， x1 x2 x3 等等都属于凸集内的点，
如果收敛 并且和也在凸集内，就说 视野更凸集

积分扩展：
系数在C上的积分等于1；
系数*x 的积分结果仍然在集合内

概率扩展(最一般的情况)：
C 属于Rn 是凸集， x是随机变量，
x 属于 C 的概率是1
那么 Ex 属于C
事实上 这里的形式包含了上述的特殊情况，
举例： 如果x 是两点分布， 就回退到了两个点的简单的凸组合

2.1.5 锥

系数为正即可（非负的线性组合)

集合C的锥包 是C中严肃 的所有锥组合的集合

2.2 重要的例子

• 空集，任意一个点 ， 全空间Rn 都是Rn 的纺射子集
• 任意直线是仿射的。如果直线通过零点，那就成为了自空间， 也是凸锥
• 一条射线 是凸的 但不是仿射的
• 任意子空间是纺射的 凸锥

2.2.1 超平面与半空间

超平面是关于x的非平凡线性方程的解空间( 因为是一个仿设集合）

几何上 超平面可以解释为与给定向量的内积为常数的点的集合
也可以堪称是 法线防线为a 的超平面， 而常数b 决定了这个平面从原点的偏移
我们甚至可以写成
{x| a^T(x-x0)=0}=x0+a的正交补

一个超平面将Rn 划分为两个半空间(闭的)
半空间是凸的但是不仿射的

开半空间 定义如其名

2.2.2 球和椭球

Euclid 球 简称球
就是说 Ecuild 范数的意思
球是 凸集


以上需要一点矩阵知识

2.2.3 范数球和范数锥

Rn 中的范数

附A.1.2

非负
正定
齐次
满足三角不等式
例子说明

二阶锥的实例 冰淇凌锥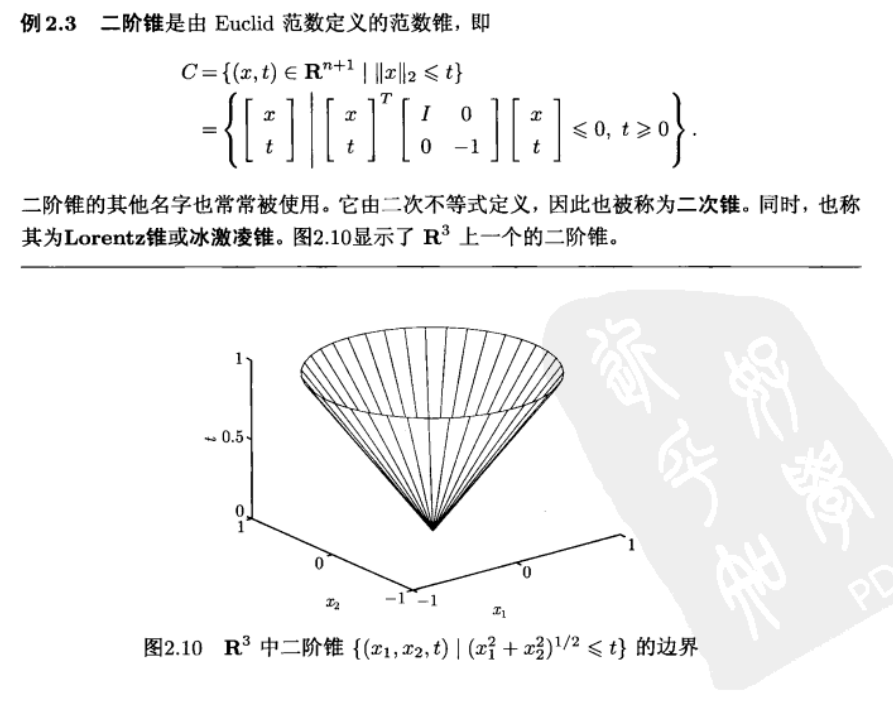

2.2.4 多面体

多面体是 有限个半空间和超平面的交集

仿射集合(子空间 超平面， 直线） 涉嫌，线段， 和半空间都是 多面体。
显而易见，多面体是凸集。

有界的多面体有时候被称为多胞形

五个半空间交集定义的多面体
形式化定义

简洁的定义如下

非负象限 具有非负分量的点的集合

单纯形

conv{v0,...,vk} 单纯形
例题2.5

k+1 个点 仿射独立 那么单纯形的维数被定义为k
单位单纯形 是由零向量和单位xiangliang 0, e1,...,en 决定的 n维单纯形。

单纯形的定义

从多面体的角度理解单纯形

首先 单纯形是 满足一定条件点(仿射独立) 的凸包

采用这种写法 简化
注意的B 的规格是 nxk 并且秩为k

不等式的角度

因为A1 A2 是随B 确定而确定的矩阵
所以这是关于x 的线性要求

多面体的凸包描述

一个凸包和一个锥包的并（）
任何一个多面体都可以如此表示

这个经典的例子说明了，使用不等式和 凸包表示一个多面体 的计算量是完全不同的

正定锥 与 半正定锥

我们认为半正定矩阵是一个凸锥

以为两个半正定矩阵的 正系数和 仍然是半正定矩阵

保凸运算

交集是保凸的

有分析 我们同样认识到半正定锥 是凸的

这种绝对值不等式 由于是两个线性不等式，我们认为他是由无数个平板的交的来 因此是凸的

事实上 一个闭集S是包含他的所有半空间的交集

仿射函数

说明了仿射函数是 保凸运算

凸集的和 部分和 是保凸运算

线性矩阵不等式的解
这里的矩阵是对称的，我们首先知道这种
是锥 半正定的 凸的
于是x 就是一种仿射映射下的原像 于是也是凸的

双曲锥 的仿射函数 到二阶锥

线性分式与透视函数

透视函数的原理:小孔成像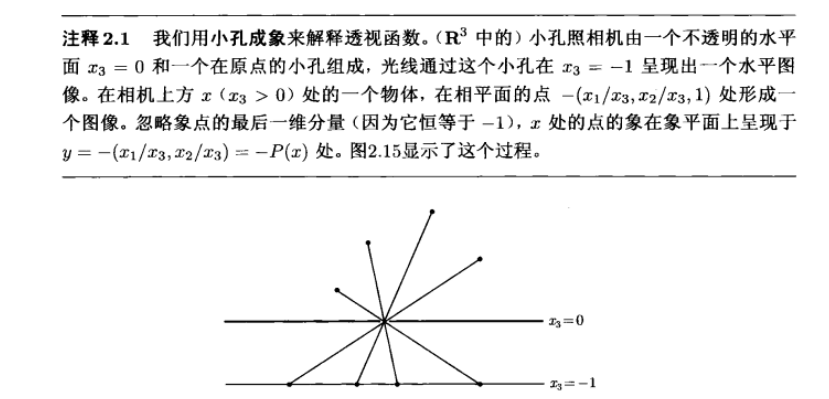

令人印象深刻

2.4 广义不等式

正常锥的定义 凸的 闭的 实的 尖的

转载于:https://www.cnblogs.com/sfzyk/p/8588573.html