一.直线和线段
设

直线:

线段:

二.仿射集(Affine Set)凸集(Convex Set)和锥(Cones)
仿射集
仿射集:通过集合

也可以理解为C包含了C中任意两点的系数之和为1的线性组合。
仿射组合:把具有


仿射集推广:
一个仿射集合包含其中任意点的仿射组合。
仿射集的例子:
直线
平面
超平面
凸集
凸集:集合C中任意两点间的线段任然在C中,那么集合C便是凸集,即
凸组合:称点


凸集推广:
一个集合是凸集等价于集合包含其中所有点的凸组合。
例子:

(最左边是凸集,右边两个不是凸集,很简单,找出两个点,看看其线段是不是有不在集合上面就行了。)
仿射集合凸集关系:
因为仿射集的条件比凸集的条件强,所以仿射集必然是凸集。\
锥
锥:对于任意的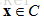
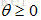
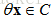
锥的例子:
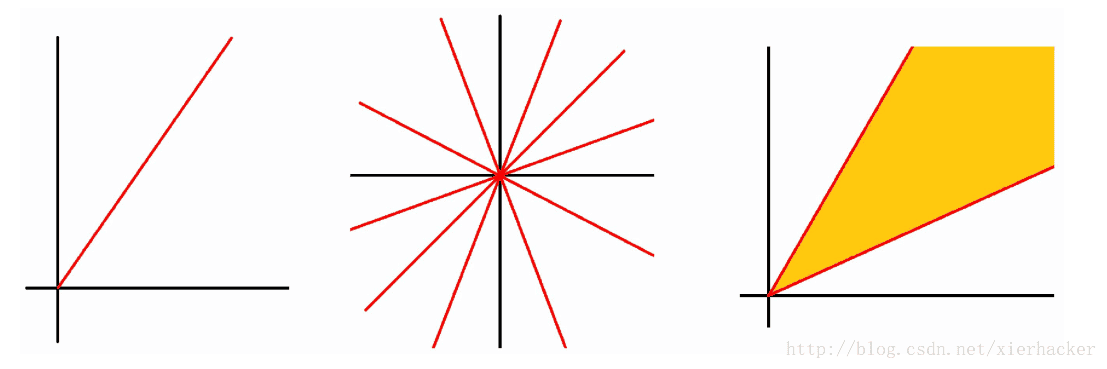
(过原点的射线,射线族,角)
凸锥:集合C既是凸集又是锥,即对于任意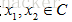
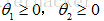
锥组合(非负线性组合):称点

三.仿射包、凸包和锥包
仿射包:由集合
也可以说,仿射包是包含C的最小的仿射集合。
仿射维数:
集合C的仿射维数为其仿射包的维数。
三角形的仿射维数为2
线段的仿射维数为1
球的仿射维数为3
凸包:集合C中所有点的凸组合的集合称为凸包,记为conv C:

也就是说集合C的凸包是能够包含C的最小的凸集。
锥包:集合C的锥包是C中元素的所有锥组合的集合。

也就是说,是包含集合C的最小凸锥。(如下图两个集合的锥包)












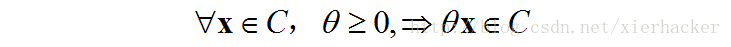
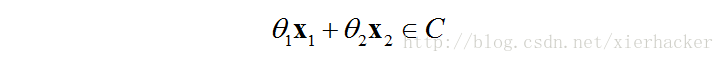




















 985
985

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








