四边形内接于圆定理_最值几何（三） 辅助圆

点击蓝字

关注我们

在数学的世界里，重要的不是我们知道什么，而是我们怎样知道什么。

–pythagoras(毕达哥拉斯)

几何最值大策略------两大公理＋三大变换

两大公理

公理一：两点之间线段最短

引申：三角形三边关系

公理二：垂线段最短

三大变换

平移、旋转、轴对称

今天我们讲解辅助圆最值问题(三角形三边关系)

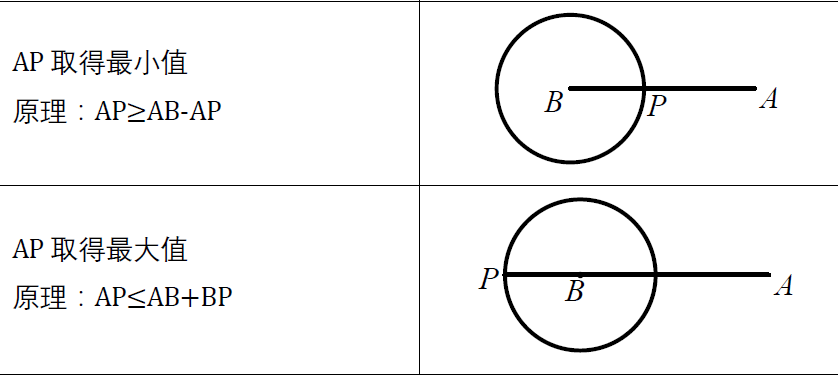
基础模型：圆外一点到圆上的最值

A为圆外一点，B为圆上动点，求AB的最值

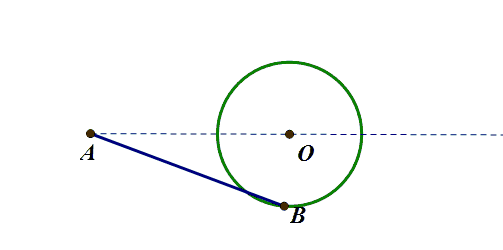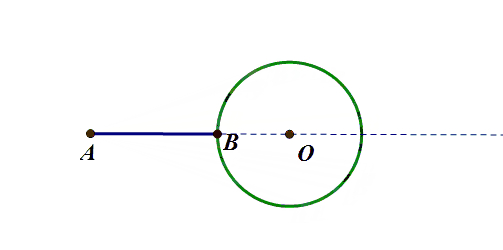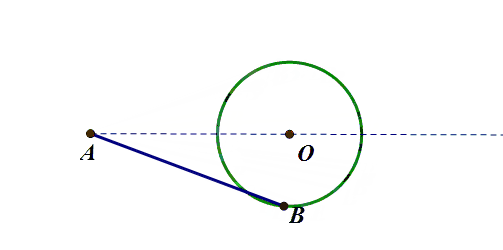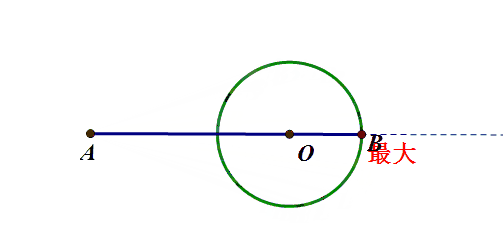
原理：三角形三边关系(第三边大于两边只差，小于两边之和)

模型3.1：定点定长

圆的定义：到定点(圆心)距离等于定长(半径)的点集合。

当题目中发现动点到定点距离不变，则动点在圆以定点为圆心，不变距离为半径的圆上。

例1 动点折叠

如图，在边长为2的正方形ABCD中，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF所在直线折叠得到△GEF，连接GC，则GC长度的最小值是                

分析：

不管点F运动到哪里，△AEF≌△GEF始终成立，则动点G到定点E的距离始终等于AE长，满足定点定长，则点G在以点E为圆心，AE为半径的圆弧上。

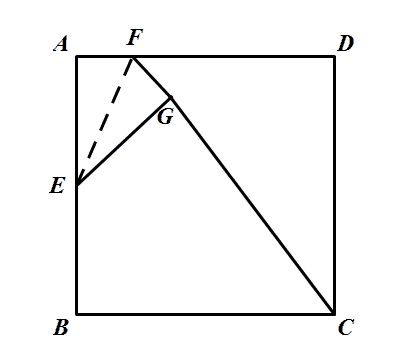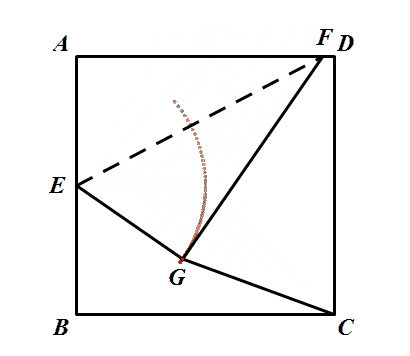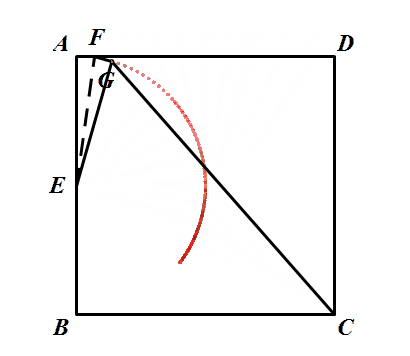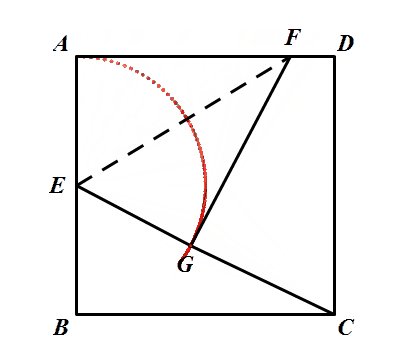
所以看基础模型，当E、G、C三点共线时，CG最短。

总结：动点折叠，轨迹为圆。

练1  动点折叠

如图，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点点N是AB边上一动点将△AMN沿MN所在的直线翻折得到△AM，连接AC，则线段AC长度的最小值是            

先仔细想想，再看答案。

模型3.2：定弦定角

圆周角定理：同弧所对圆周角相等。

圆周角定理+等弧对等弦，所以在一个三角形中，当一个角所对的边不变，且这个角的大小不变，则这个角的顶点在这个三角形的外接圆上。

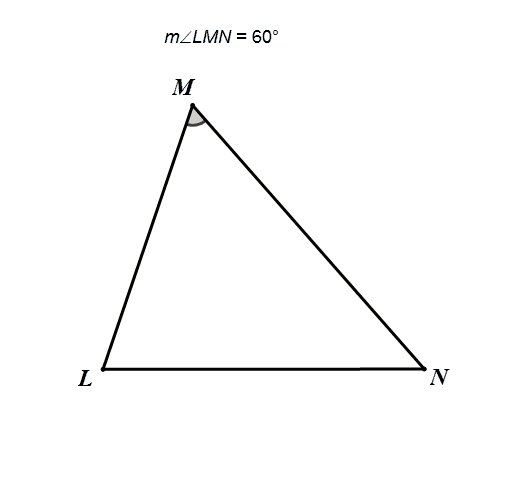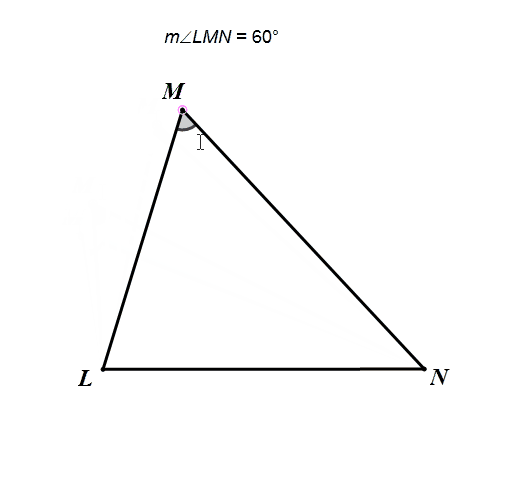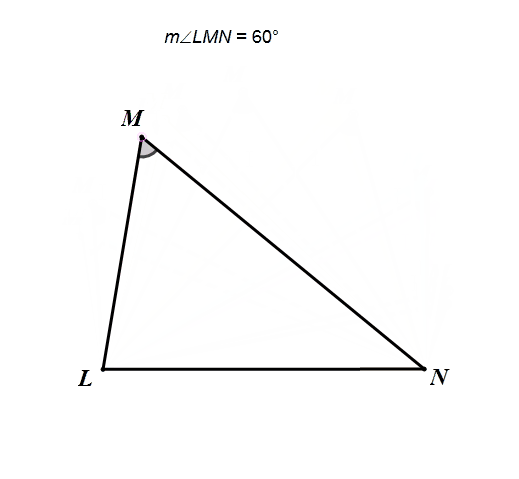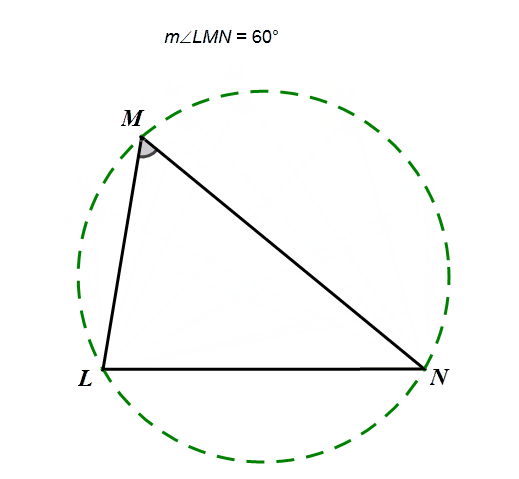
例2  定角定弦

如图，点P在第一象限，△ABP是边长为2的等边三角形，当点A在x轴的正半轴上运动时，点B随之在y轴的正半轴上运动，运动过程中，点P到原点的最大距离是________.

分析：

本题由于AB两点都是动点，分析起来比较难，我们不如改变视角，用手摁住AB不动，让坐标系动起来。

由于AB长固定，∠AOB=90°始终成立，则O点轨迹在圆上，就像这样。

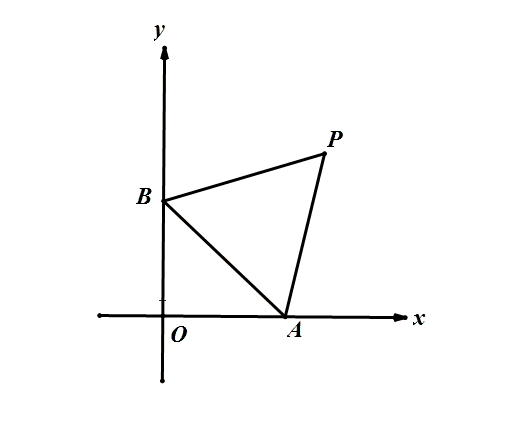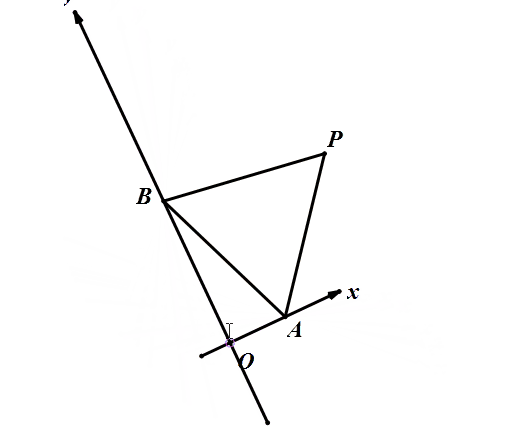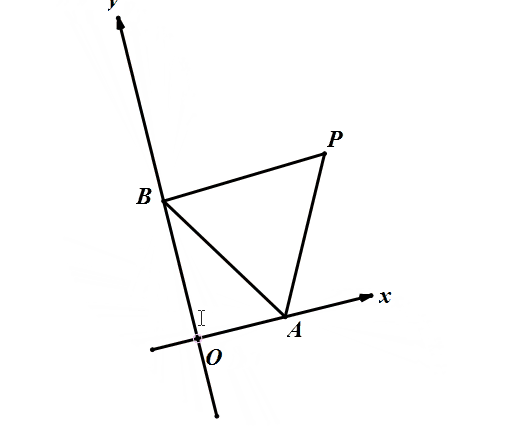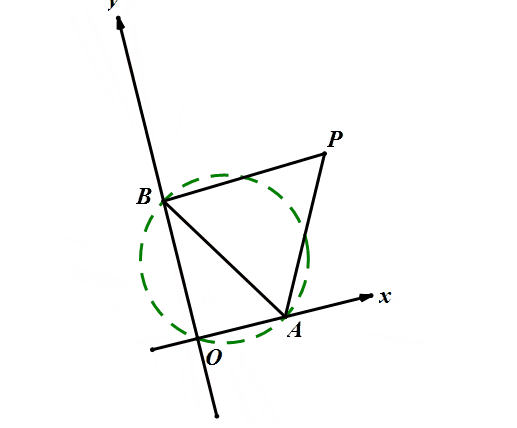
所以我们只要确定圆心，三点共线，就可以迎刃而解！

总结：定长线段移动时，可以转化参考系，化动为静，变静为动。运动是相对的，并非绝对。

模型3.3：四点共圆

我们知道圆的内接四边形对角互补。

那什么样的四边形四点共圆呢？

第一类：对角互补四边形(∠A+∠C=180°)

第二类：等角对同边(∠BAC=∠BDC)

第三类：反8相似(△ABO∽△DCO)

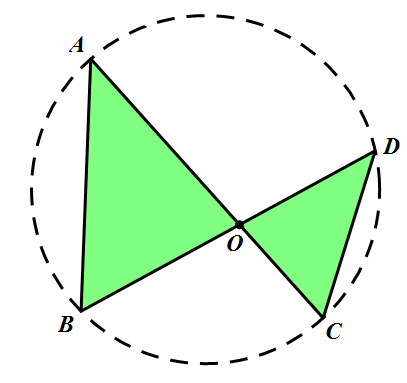
例3  找找共圆

正方形ABCD中，∠EAF=45°，交BD于G、H

找找哪四个点共圆？

解析：

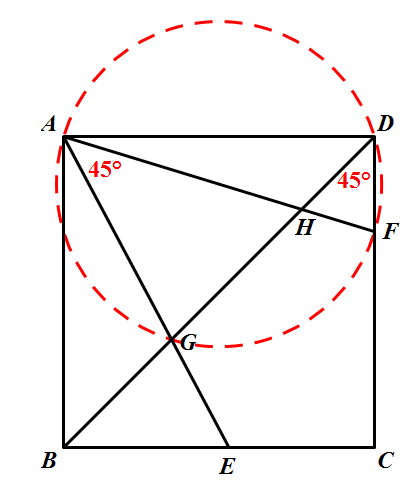
A、G、F、D四点共圆

A、B、E、H四点共圆

总结：熟悉上述三类模型，即可找到四点共圆。

最后，提一个小问题：辅助圆的类型有哪几类核，能总结出来吗？

最值问题先告一段落，后续还有更精彩的专题，敬请期待！

往期精彩回顾：

最值几何(一)

最值几何(二)---垂线段最短

你不知道的尺规作图(一)

你不知道的尺规作图(二)

你不知道的尺规作图(三)

你不知道的尺规作图(四)

你不知道的尺规作图(五)

老师加的那条辅助线为什么我没想到？I-基础篇

老师加的那条辅助线为什么我没想到？II-探究

“一边一角”全等构造-实战破题篇(1)

“一边一角”全等构造-实战破题篇(2)

“一边一角”全等构造-实战破题篇(3)

扫码关注我们

微信号｜天才数学战

球分享

球点赞

球在看