四边形内接于圆定理_「奥数」蝴蝶定理

蝴蝶定理(Butterfly Theorem)，是古代欧氏平面几何中最精彩的结果之一。这个命题最早出现在1815年，由W.G.霍纳提出证明。而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号，题目的图形像一只蝴蝶。这个定理的证法不胜枚举，至今仍然被数学爱好者研究，在考试中时有各种变形。

蝴蝶定理(Butterfly Theorem)：设M为圆内弦EF的中点，过M作弦AB和CD。设AD和BC各相交EF于点P和Q，则M是PQ的中点。

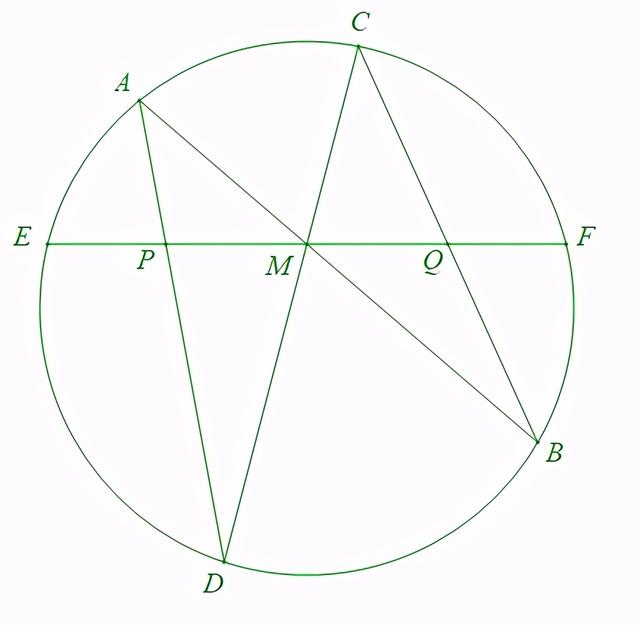
【简析】

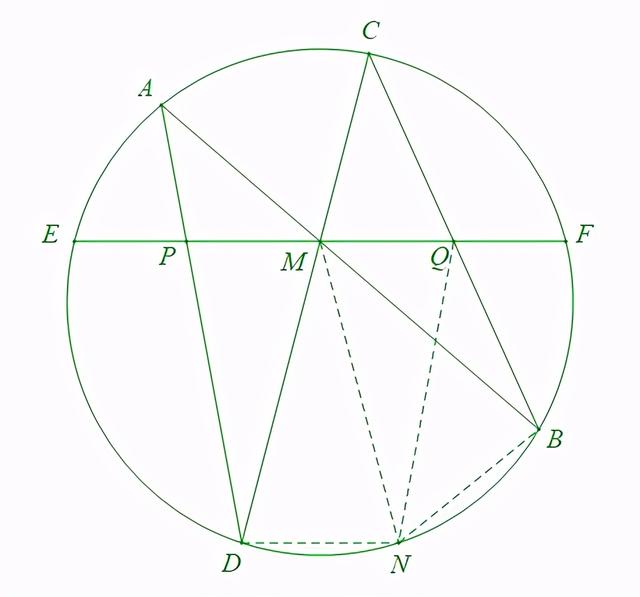
如图，过点D作弦DN∥EF，连接MN、QN和BN，

四边形BCDN为圆的内接四边形，

所以∠CDN+∠CBN=180°，

根据圆的对称性，易证MD=MN，∠DME=∠NMF，

那么可以得到∠QMN=∠MND=∠MDN，

所以∠QMN+∠CBN=180°，

则M、N、B、Q四点共圆，

∠MNQ=∠MBQ=∠ADC，

那么可得△DMP≌△NMQ(ASA)，

进而得到MP=MQ。