四边形内接于圆定理_几何综合之托勒密定理

几何综合题中常出现判断两条或三条线段的数量关系的题目，其中共顶点三线段数量关系的证明，一直是北京乃至全国初中几何考题中的常客，从初二上学期的等边三角形到初二下学期四边形，此类考题考察都非常广泛，其中托勒密定理的应用尤为突出！ 今天我们一起来探究，什么是托勒密定理？它又将如何应用！

托勒密定理：圆内接四边形中，两条对角线的乘积等于两组对边的乘积之和

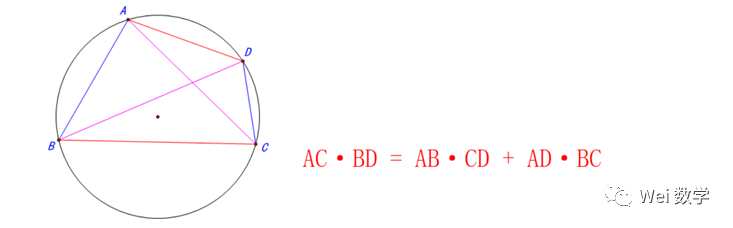
定理的证明需要构造相似，用到两组相似?，结合证明

过程如下：

当然我们还可以从不同的构造方向，分别以点A点B点C三点为顶点，构造相似?，同样可以得出结论，不妨来动手试一试：

托勒密定理的逆定理：在凸四边形ABCD中，若两条对角线的乘积等于两组对边的乘积之和，则四边形ABCD内接于圆。

拓展四点共圆情况：

1. 若四个点到一个定点的距离相等，则这四点共圆(圆的定义)

2. 同斜边的直角三角形的四个顶点共圆(直径所对圆周角是直角)

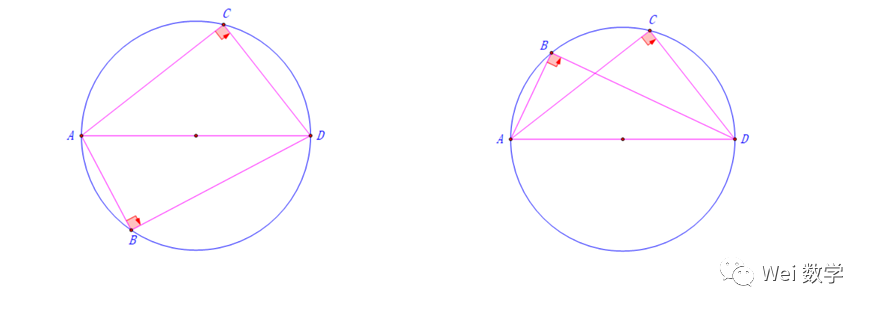
3. 若一个四边形的一组对角互补(和为180°)则这四个点共圆

(圆内接四边形对角互补)

4. 若一个四边形的外角等于它的内对角，则这个四边形的四个顶点共圆

5. 若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两端共圆(在同圆或等圆中，同弧或等弧所对圆周角相等)

在考试中常考题型，熟练后，秒出结论，不成问题！

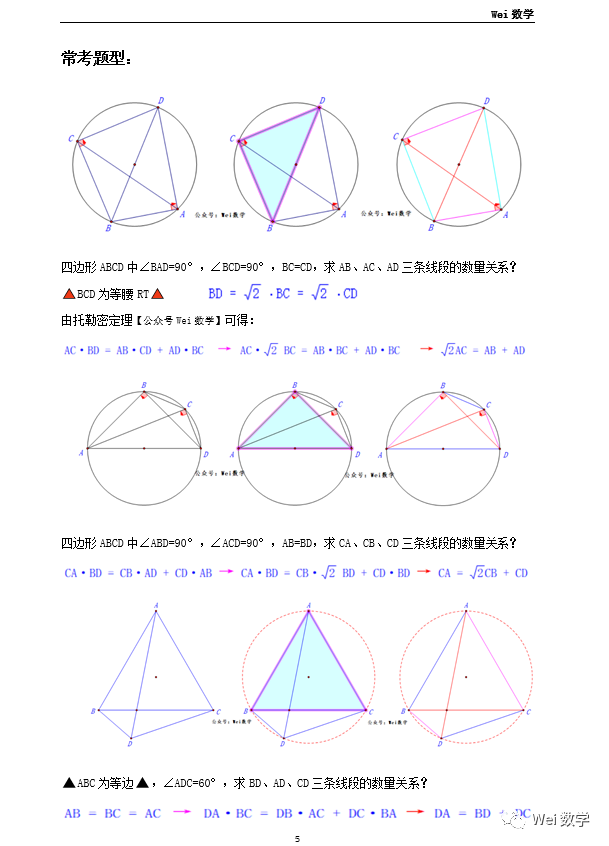
托勒密定理不止在初中几何中应用广泛，在高中解三角形和圆锥曲线中也有很多妙用！

整理了部分北京初中几何考题，来练练手：

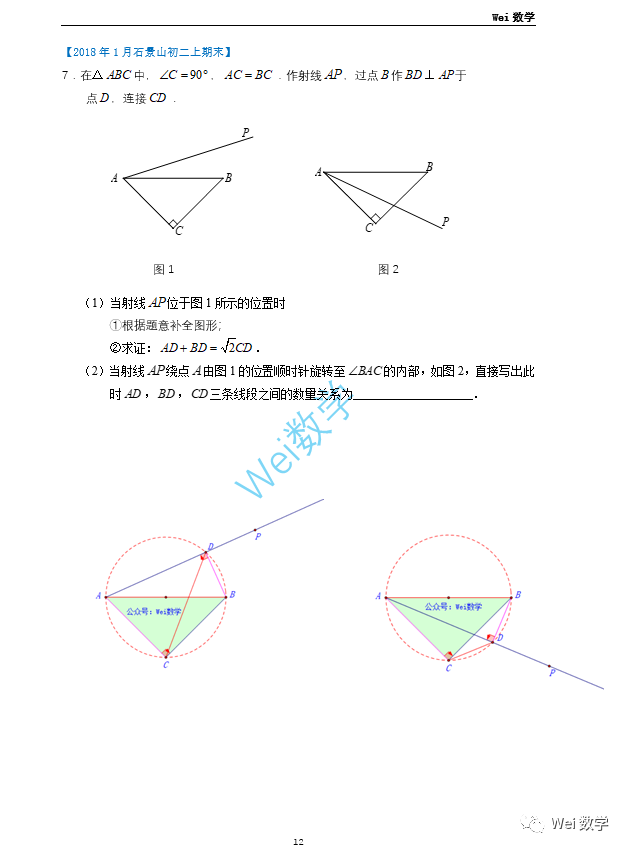
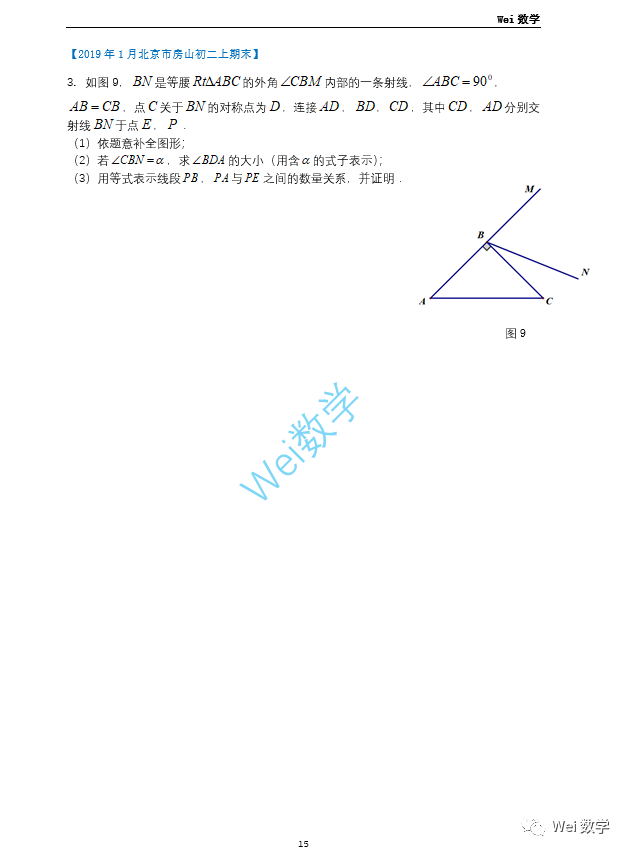
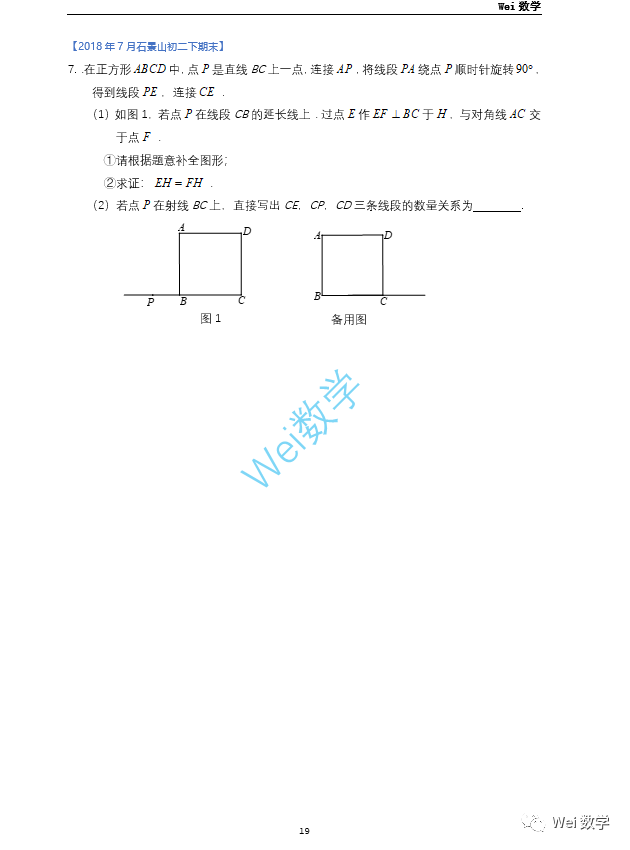
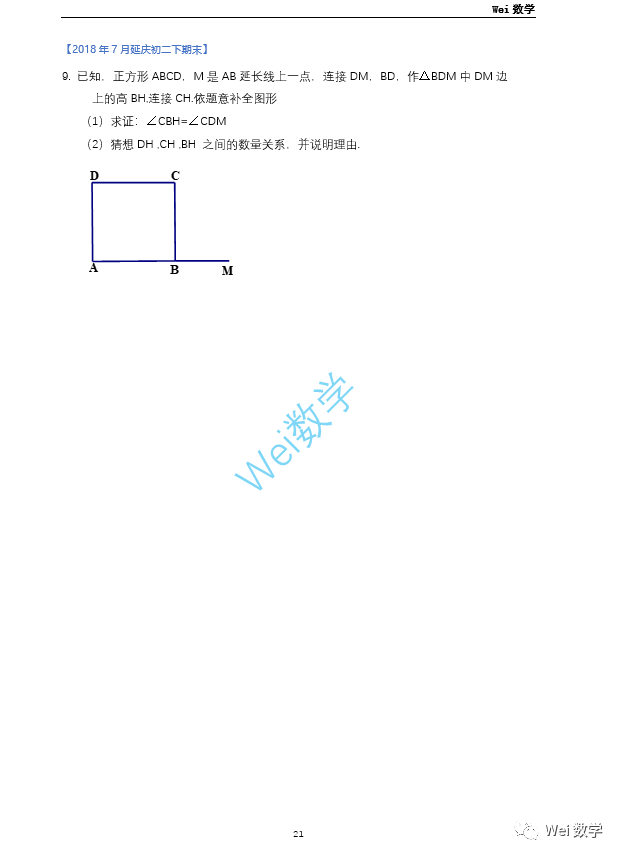
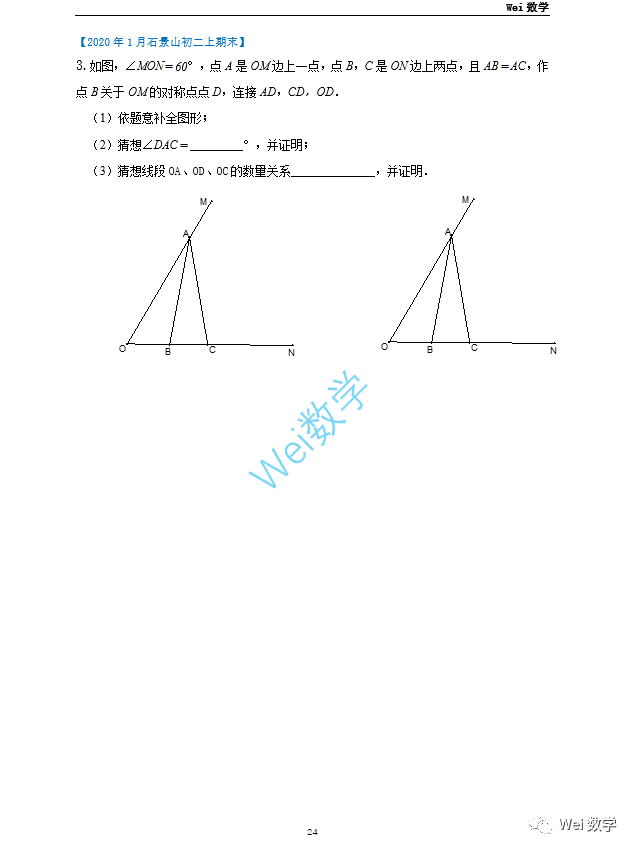
非常经典的20年东城二模，此题答案在如下推荐链接：

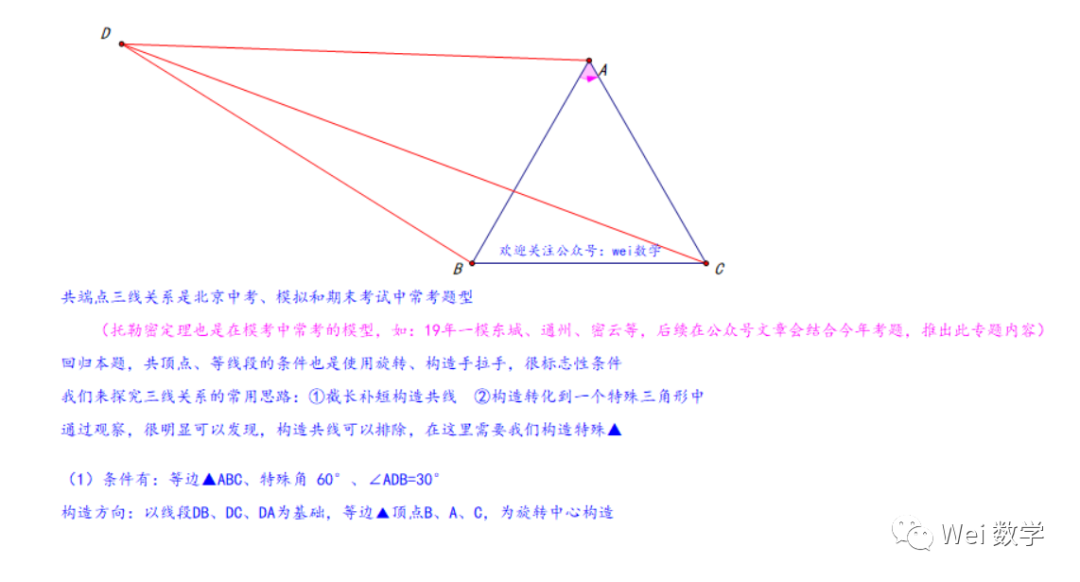
2019-2020北京市初三二模数学东城、西城选填核心题目对比，几何综合、新定义详解

往期推荐：

一题多解，品一品60°和45°几何综合

几道有意思的几何综合

专题讲义暂不提供电子版。