四边形内接于圆定理_圆的重点和难点解析

圆的重点和难点解析

1、圆：

(1)圆可以看作线段OA绕着一个端点O旋转一周，另一个端点A所形成的的图形。——运动的角度

点O为圆心，OA为半径   记作⊙O

(2)圆可以看作到定点的距离等于定长的点的集合。——集合的角度

         定点——圆心          定长——半径

2、弦：连接圆上任意两点的线段叫做弦。

               经过圆心的弦叫做直径。

3、弧：圆上任意两点间的部分叫做圆弧，简称弧。

            圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

4、优弧和劣弧：小于半圆的弧叫做劣弧；大于半圆的弧(用三个字母表示)叫做优弧。

5、等弧：在同圆或等圆中，能重合的弧叫等弧。

6、对称性：既是轴对称图形又是中心对称图形。

重点：应用是圆中的半径所构成等腰三角形的进行计算。

典型题目：

如图，⊙O的直径BA的延长线与弦DC的延长线交于点E，且CE＝OB，

已知∠DOB＝72°，求∠E

解：连接OC，设∠E=x

∵ CE＝OB，OC＝OB

∴ ∠E= ∠1=x

∵∠2= ∠E+ ∠1=2x

∵ OC＝OD

∴ ∠2= ∠D=2x

∵ ∠DOB=∠ E+∠D=3x= 72°

∴x=24°

∴ ∠E= 24°

教学重点：

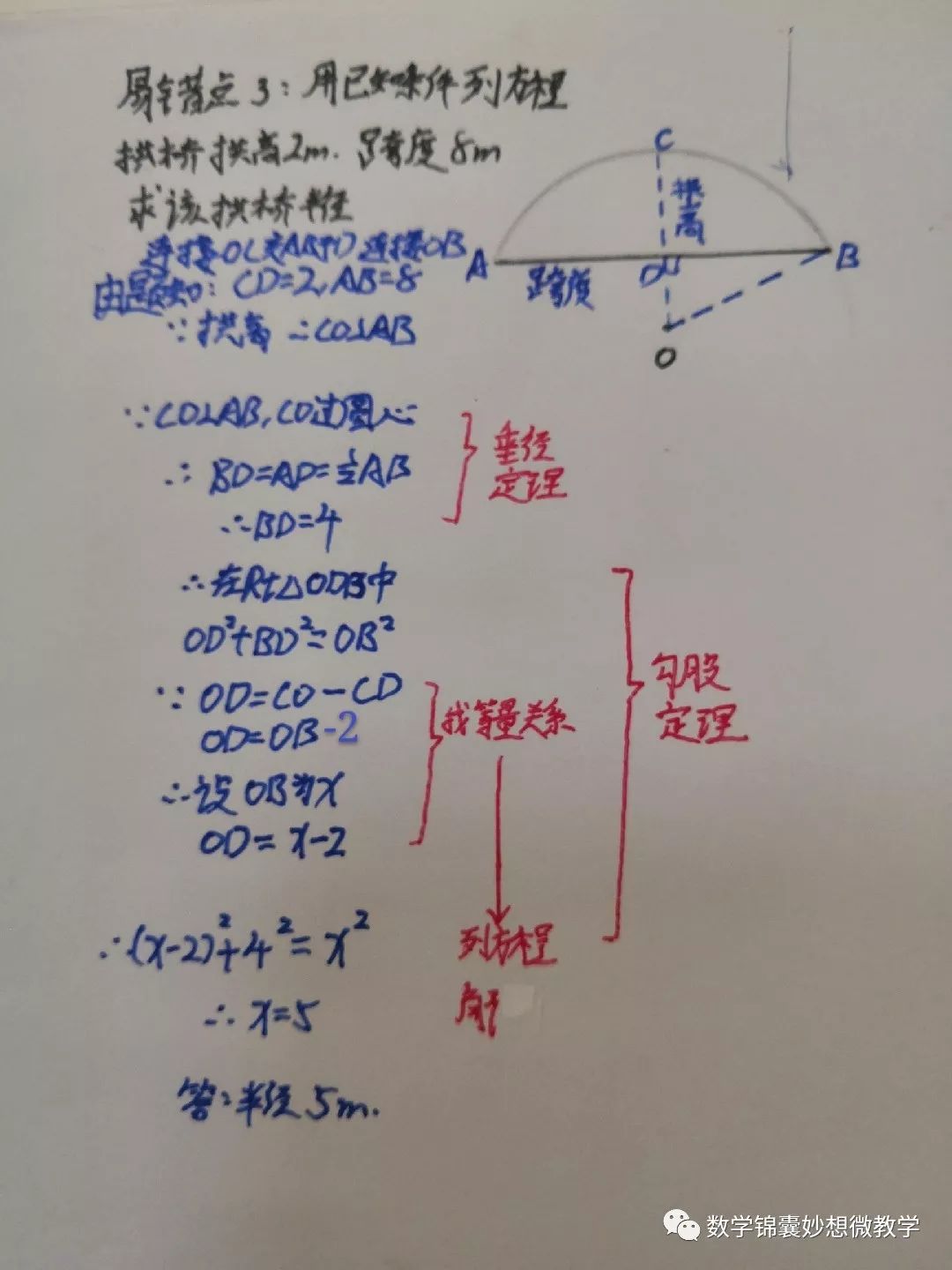
垂径定理：垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。

明确垂径定理的一个推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧。

根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备上述五个条件中的任何两个条件都可以推出其他三个结论。

      垂径定理及其推论反映了圆的重要性质，是圆的轴对称性的具体化，也是证明线段相等、角相等、垂直关系的重要依据。

典型习题：

难点：

易错点：

1、定义：顶点在圆心的角叫做圆心角。(如：∠AOB和∠A‘OB’ )

2、圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等.

3、推论：同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．

典型习题：

1、定义：顶点在圆上，并且两边都和圆相交的角叫圆周角．

2、圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半. ∠AOB=2∠ACB

3、推论1：同弧或等弧所对的圆周角相等．∠ACB=∠AC’B

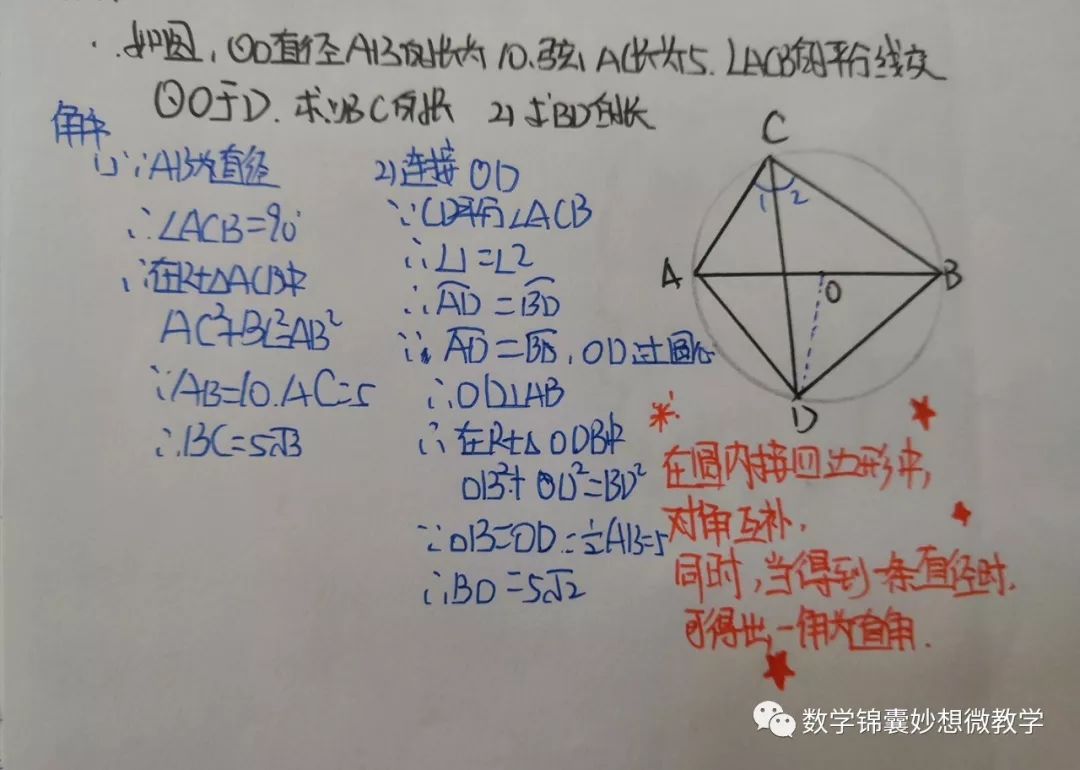
推论2：半圆(或直径)所对的圆周角是直角.

推论3：90°的圆周角所对的弦是直径

典型习题：

4、圆内接多边形：如果一个多边形的所有顶点都在一个圆上，这个多边形

叫做圆内接多边形，这个圆叫做这个多边形的外接圆

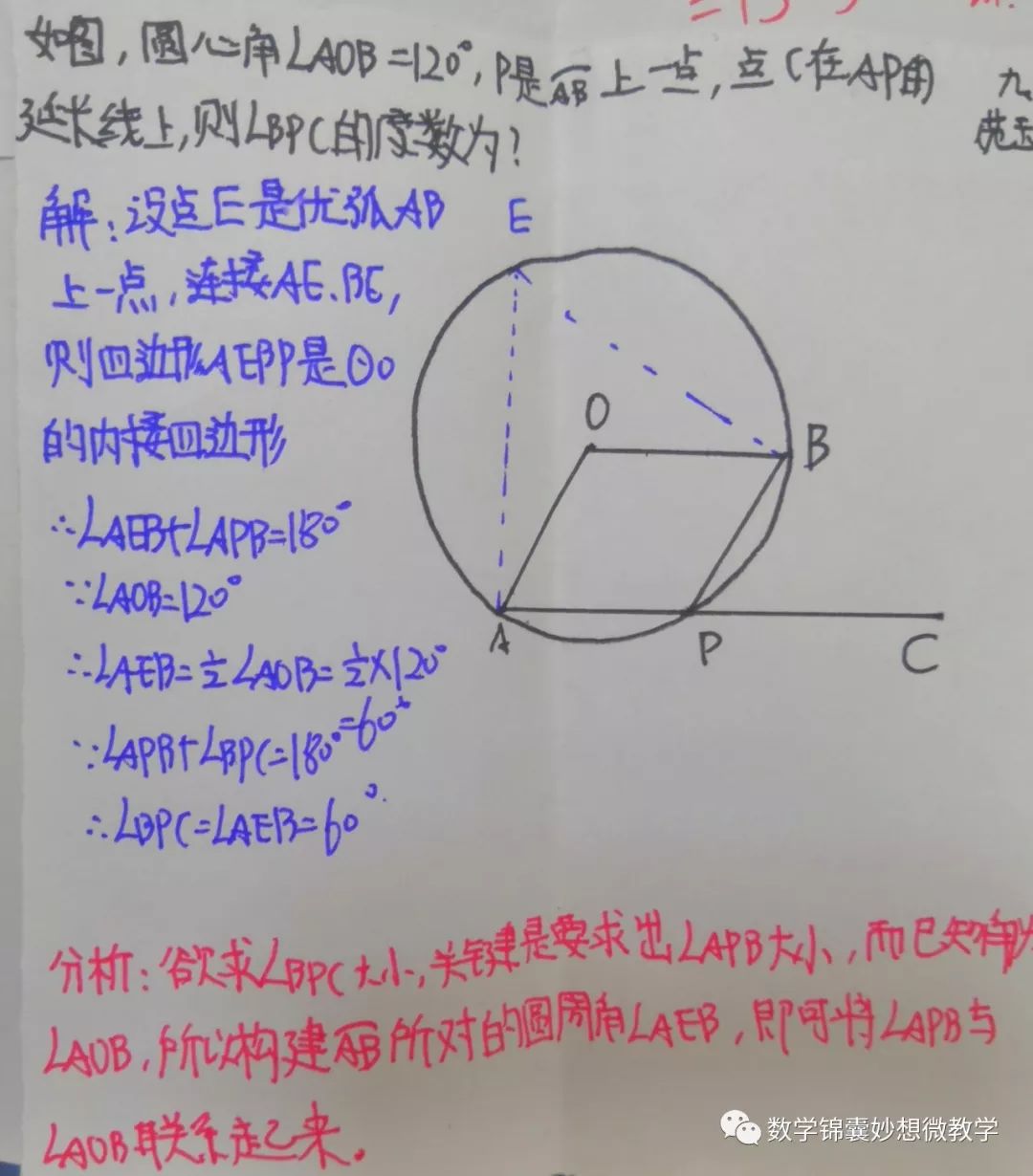
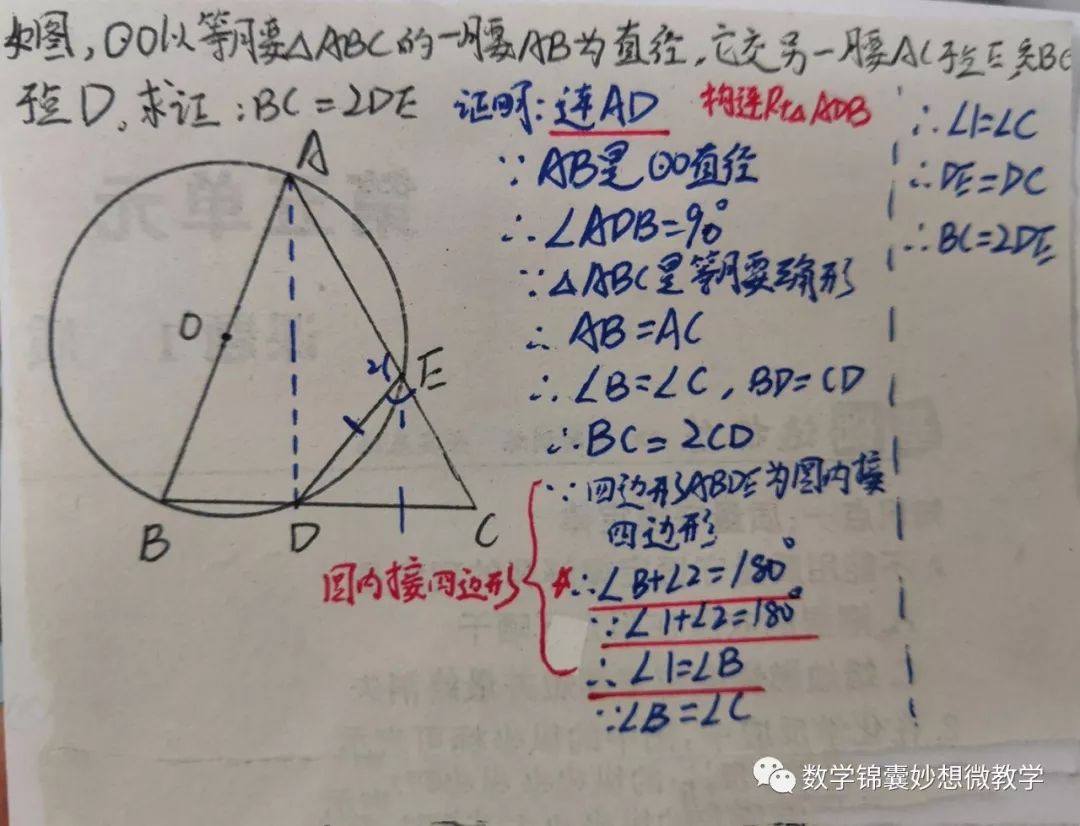
5、圆内接四边形：圆内接四边形的对角互补。

∵圆内接四边形ABCD

∴∠ABC+∠ADC=180°

圆内接四边形的外角等于内对角

∵圆内接四边形ABCD

∴∠ADE=∠B

典型习题：

设⊙O的半径为r，点到圆心的距离为d，则有：

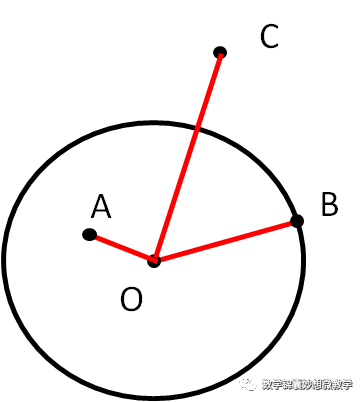
典型习题：

如图，Rt△ABC中，∠C=90°，CD⊥AB于D，AC=3，AB=5，以C为圆心，AC长为半径画圆，试指出A、B、D与⊙C的关系。

解：∵ ∠C=90°,AC=3，AB=5

∴由勾股定理得BC=4

∵CD⊥AB于D

∴由△ABC面积得CD=2.4

∵以C为圆心，AC长为半径画圆

∴AC= r =3 ，点A在圆上

   BD=4﹥r，点B在圆外

   CD=2.4 ﹤ r，点D在圆内

典型习题：

在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与直线AB有怎样的位置关系？为什么？

 (1)r=2cm；

 (2)r=2.4cm

 (3)r=3cm。

解：∵ ∠C=90°,AC=3cm，AB=5cm

∴由勾股定理得BC=4cm

∵ CD⊥AB于D

∴由△ABC面积得CD=2.4cm

∵以C为圆心

∴圆心到直线AB的距离d=CD=2.4cm

∴ r=2cm时，d﹥r，⊙C与直线AB相离；

   r=2.4cm时，d=r，⊙C与直线AB相切；

   r=3cm时，d﹤r，⊙C与直线AB相交。

6、切线的判定定理：经过半径的外端点并且垂直于这条半径的直线是圆的切线。

∵OA是半径，       

    OA⊥m于点A

∴直线 m是⊙O的切线

典型习题：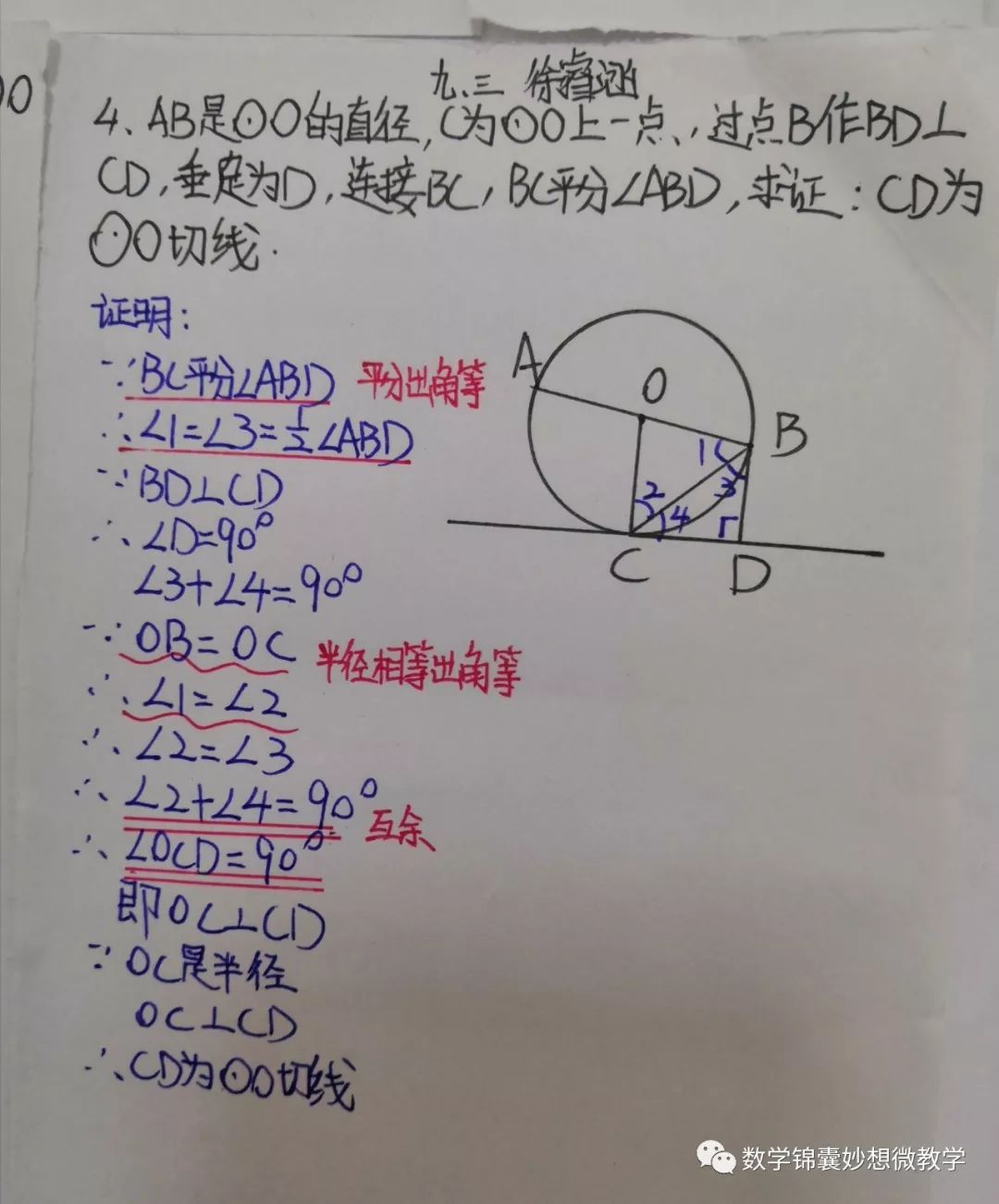

7、切线的性质定理：圆的切线垂直于过切点的半径．

∵直线 m切⊙O于点A

∴OA⊥直线 m

归纳：切线的判定方法有三种：

①直线与圆有唯一公共点；

②直线到圆心的距离等于该圆的半径；

③切线的判定定理．

8、切线长的定义：经过圆外一点作圆的切线，这点和切点之间的线段的长，

叫做这点到圆的切线长。(PA、PB)

9、切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，

这一点和圆心的连线平分两条切线的夹角。

∵PA，PB是圆的切线

∴PA=PB，

      ∠APO=∠BPO

切线长定理的拓展结论：

∵PA，PB是圆的切线

∴PA=PB，

  ∠APO=∠BPO

∴OP ⊥AB

 ∴AE=BE

M为弧AB中点

典型习题：

10、三角形内切圆：与三角形各边都相切的圆叫做三角形的内切圆。

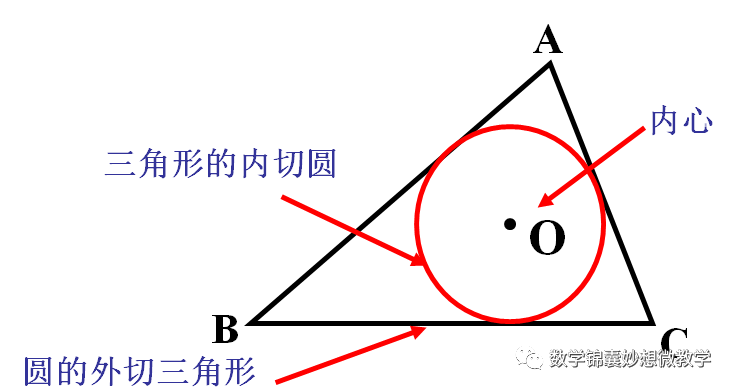
三角形内切圆的圆心O叫做三角形的内心，内心是三角形三条角平分线的交点，它到三边距离相等。

结论：

典型习题：

1、△ABC中，⊙O是△ABC的内切圆，切点是D，E，F，AB=12，BC=10，AC=8，求AD、BE、CF

解：设AD=x

∵ ⊙O是△ABC的内切圆

∴AD=AF=x

    BD=BE=12-x

    CE=CF=8-x

∴BC=BE+CE=12-x+8-x=10

∴x=5

∴AD=5,BE=12-5=7,CF=8-5=3

2、Rt△ABC中，∠C=90°，⊙O是△ABC的内切圆，切点是D，E，F，AB=13，BC=5，AC=12，求⊙O半径。

解：方法1：

方法2：

(1)定义：各边相等,各角也相等的多边形叫做正多边形。

(2)正n边形与圆有密切的关系：把圆分成n等分(n≥3),顺次连接各分点所得的多边形是这个圆的内接多边形。

(3)正多边形的中心:正多边形的外接圆的圆心.

(4)正多边形的半径:外接圆的半径R(OA和OB)

(5)正多边形的边心距:中心到正多边形的一边的距离r(OE)(内切圆半径)

(6)正多边形的中心角：正多边形的每一条边所对的圆心角ɑ( ∠ AOB)

(7)相关计算公式：

设边长为a，周长为L

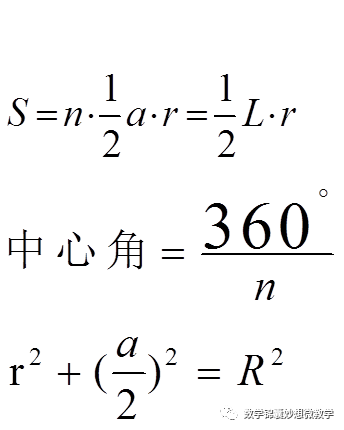
典型习题：

1、已知等边△ABC的半径为2，求它的边心距、边长，周长、面积。

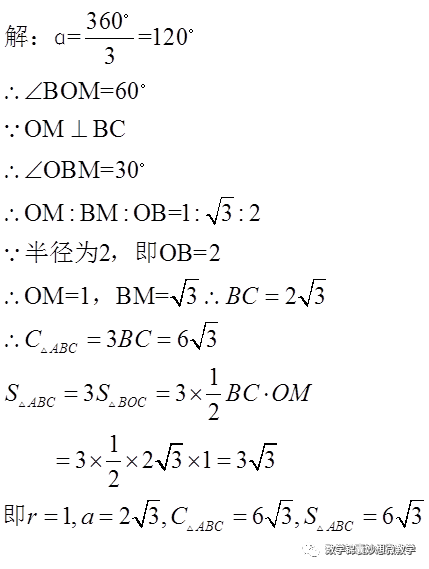
2.已知正四边形的边长为2，求它的外接圆的半径、内切圆半径、周长、面积。

3.已知六边形的边心距为 2cm，求它的边长、外接圆的半径、周长、面积。

难点：求半径相等的正三角形、正四边形、正六边形的面积比。

典型习题：

1.已知：扇形的圆心角为150°，半径为3，求扇形的弧长。

易错点：

2．已知：扇形的弧长为6π ，圆心角为120°，求扇形的面积。

3．一个扇形的弧长是6π ，面积是12π ，求扇形的圆心角。

(1)圆锥的侧面展开图是一个扇形。

(2)母线：这个扇形的半径(圆锥有无数条母线)

(3)圆锥底面圆周长：这个扇形的弧长

(4)圆锥的高:连结顶点与底面圆心的线段叫做圆锥的高h

                   h2+r2=R2

(5)圆锥的侧面积:

  S侧= 1/2母线长×底面圆的周长

     = 1/2R ×2πr= πrR

(6)圆锥的表面积：

  S表=S侧+S底=πrR+πr2

典型习题：

如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，求圆锥的底面半径.

一审：三班黎昌翰、张潇博、郭煜航；二审：四班曹洛萌、邓雨含、王涵。

感谢六位小朋友。

有趣的数学在等你 长按扫码关注