犀牛给曲线增加控制点_如何绘制最简曲线

   Rhinoceros犀牛的曲线称为Nurbs曲线(Non-Uniform Rational B-Splines)，非均匀有理B样条。在如何绘制最简曲线前，首先应该掌握Rhinoceros犀牛曲线的基本概念：控制点、阶数、节点，(如下图所示)。

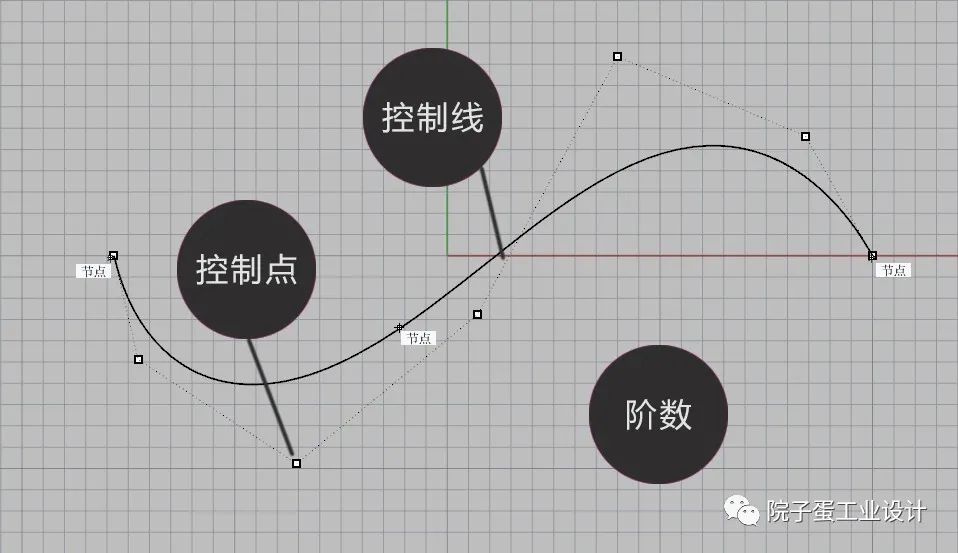
    控制点：两个控制点是由控制线连接的，控制点左右两侧的曲线会随着控制点的移动发生变化；Rhinoceros犀牛曲线中有包括控制点和编辑点，控制点在曲线外，又称为外壳线，编辑点在曲线上。 

     阶数(Degree)：又称为度数，是一种数学模型，这个指数决定了曲线的光顺程度。

     节点：一般是曲线上的多余信息，控制点数减去阶数等于节点数；添加节点，控制点会增加，删除节点，控制点会减少。

1、什么是最简曲线？

   最简曲线是一条Nurbs曲线的控制点数减去阶数的数值是1；这样的曲线只有在曲线的首端和末端分别有一个节点，中间没有节点，又称之为单跨距(英文单span)的曲线；节点是多余的信息，因为曲线的中间没有节点，这样的曲线是没有信息冗余的，(如下图所示)。

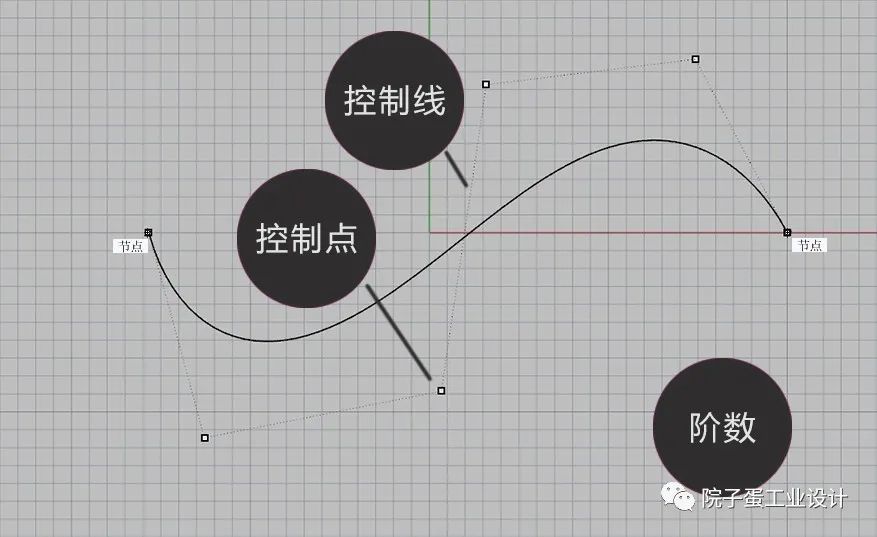
   该条曲线是6个控制点，阶数是5，满足控制点数减去阶数的数值是1，是一条最简曲线，(如下图所示)。

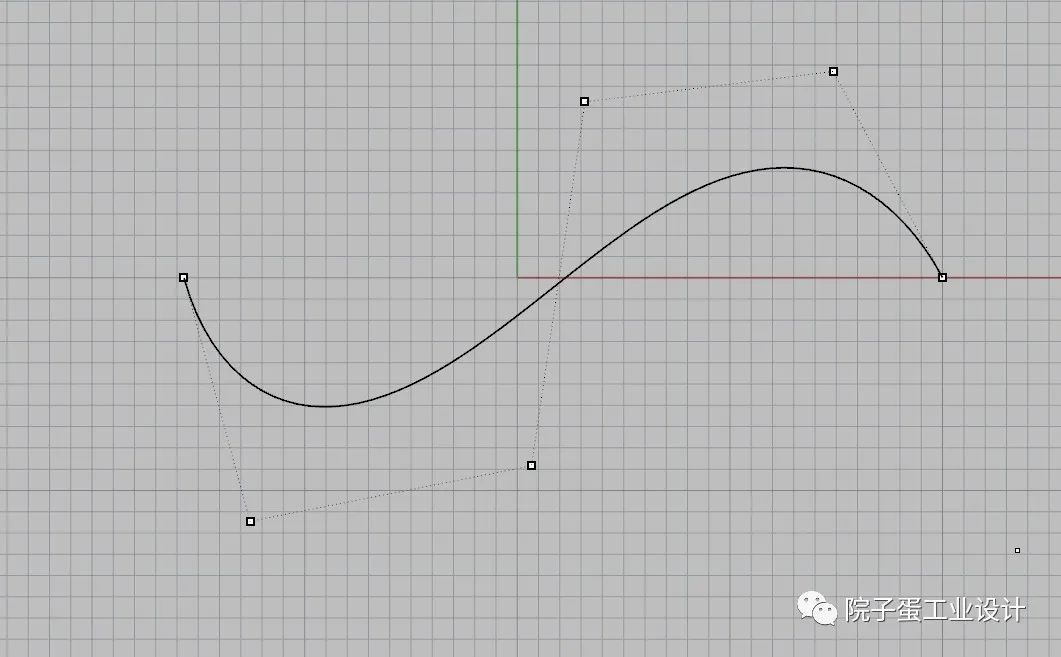
2、如何绘制最简曲线？

   绘制最简曲线的方法包括：控制点曲线画法和内插点曲线画法两种方法。两种方法我们都是以5阶为例。

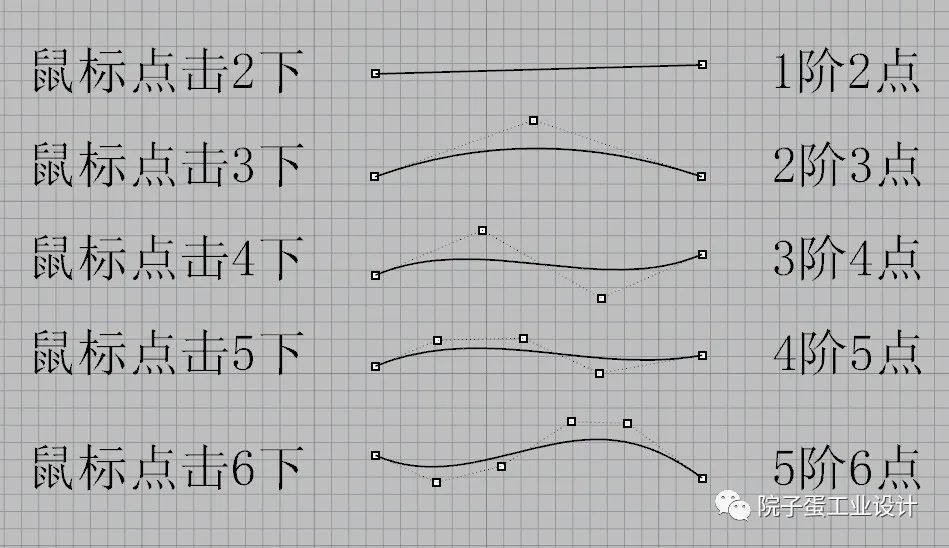
   1、控制点曲线画法：在控制点曲线命令栏(阶数(D)=)输入数值5并且在任一二维视图画曲线。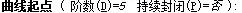鼠标点击2下会生成一条1阶2点的曲线；鼠标点击3下会生成一条2阶3点的曲线；以此类推直到鼠标点击6下以下都会生成相应阶数和点数的最简曲线，满足控制点数减去阶数的数值是1，(如下图所示)。

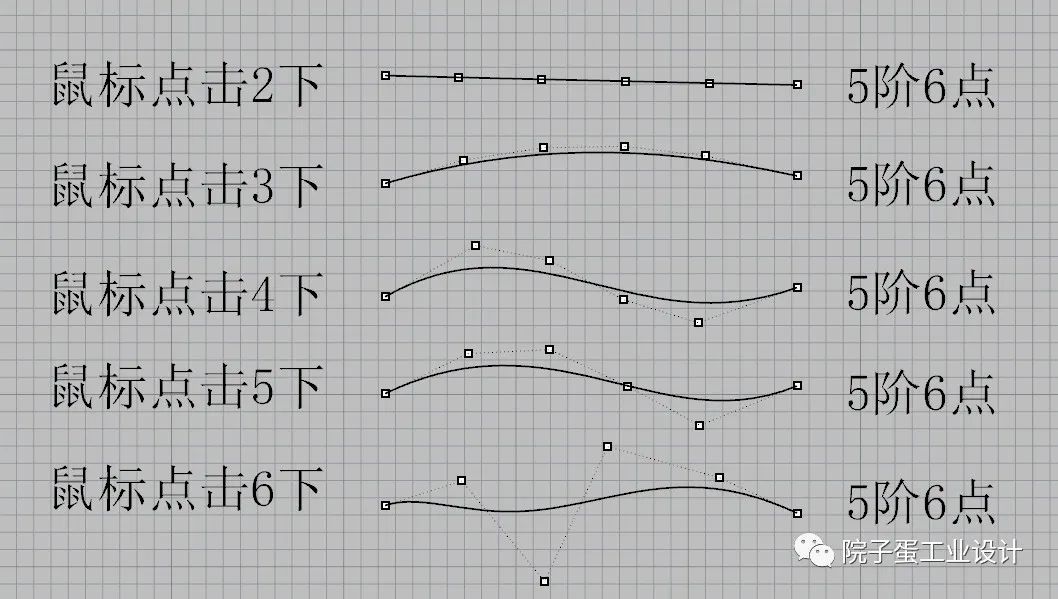
   2、内插点曲线画法：内插点曲线(阶数(D)=)输入数值5，(节点(K)=)选择均匀 并且在任一二维视图画曲线。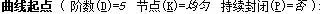鼠标点击2下会生成一条5阶6点的曲线；鼠标点击3下同样会生成一条5阶6点的曲线；以此类推直到鼠标点击6下以下都是生成一条5阶6点的最简曲线，满足控制点数减去阶数的数值是1，(如下图所示)。

虽然(阶数(D)=)输入数值都是输入5，控制点曲线画法和内插点曲线画法的结果是不一样，但是都可以画出最简曲线。 以上都是以阶数5作为案例，通过实验性发现Rhinoceros犀牛在控制点曲线的画法的情况下一般阶数在1-11，只要鼠标点击的次数不超过(阶数(D)=)输入的数值+1，都可以生成相应阶数和控制点数的最简曲线。在内插点曲线画法的情况下，内插点曲线画法(阶数(D)=)输入的数值只能是奇数(1、3、5、7、9、11)这几个数值，而且数值3还是特例，只要鼠标点击的次数不超过(阶数(D)=)输入的数值+1，生成的最简曲线的阶数都是(阶数(D)=)输入的数值，控制点数是(阶数(D)=)输入的数值+1。掌握了这些规律就可以任意画最简曲线。 在Rhinoceros犀牛中的曲线不需要过多的控制点就可以描述产品的造型，一般情况下产品的模型所有成面曲线都可以用最简的曲线。最简曲线的画法可以使得产品模型的曲面更加光顺并且质量更好，成为曲线生成高质量曲面的基础。