核密度中对窗框h的估计用R语言_密度泛函理论(二)

分子模拟学习，请点击蓝字关注~

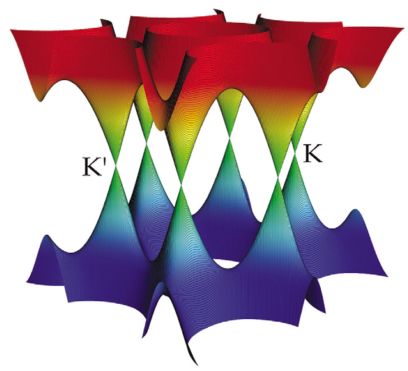
(石墨烯的价带与导带，Materialstoday, Vol 10, 1-2, 2007)

在密度泛函理论的第一篇文章中，我们介绍了Kohn-Sham将多电子体系中的能量进行分解重组，最终建立了能量泛函。除了非关联动能项，核势能，Hartree能，交换关联能都表达成了电子密度的函数，而非关联动能项表达为非关联轨道波函数的泛函，如下式所示：

其中各项的表达式为：

---

Kohn-Sham方程

下面我们需要求解能量泛函的最小值，也就是体系的基态，在求解能量最小值的时候，需要注意到系统的波函数需要满足正交关系，因此该极值为条件极值。正交限制条件为：

利用拉格朗日乘子法求解极值：

展开上式，代入各项的变分：

最终，欲使所构造的拉格朗日泛函的变分为0，需要满足：

其中拉格朗日乘子是由于各个轨道的正交化而引入的，因此可以看做不同轨道的特征值，也就是各个轨道的特征能量，因此Kohn-Sham方程最终化简为：

上式就是著名的Kohn-Sham方程，在利用密度泛函理论进行计算的时候，实际的计算都是根据辅助哈密顿量HK-S来进行计算的。

交换关联泛函

利用Kohn-Sham方程求解多电子体系的能量及电子密度的一个重要的前提是：已知的交换关联泛函Uxc。在密度泛函理论中，所有的量在理论上都是精确的，只有交换关联泛函采用的是近似方法得到的。通常的近似方法有局部密度近似(LDA)和广义梯度近似(GGA)。

1. 局域密度近似

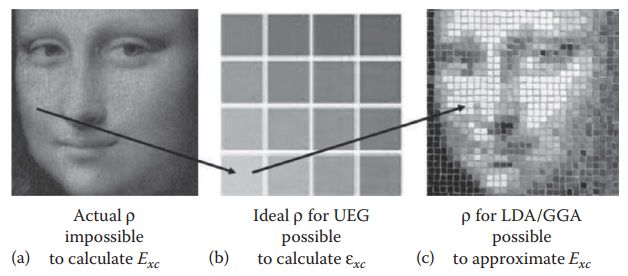
(Book:Computational Materials Science, June Gunn Lee)

局域密度近似的主要思想是，电子在均匀场中将表现为均匀的电子密度，其交换关联能是可以用量子蒙特卡洛算法精确计算的，当外界势场变化幅度不剧烈时，在局域采取均匀的电子密度来计算交换关联能。

在均匀场中，交换能的表达式为：

关联能的表达式为：

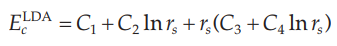
其中Ci都为拟合的常数，rs是与电子密度有关的量，表达式为：

最终交换关联能都表达为电子密度的函数，那么就可以代入Kohn-Sham方程进行计算了。

利用局域密度近似也可以处理考虑电子自旋的电子密度：

局域密度近似LDA方法在早期的DFT计算中被广泛使用，但它在计算下列问题时存在一定的误差：

1、计算晶格常数时会通常偏小，因此体系的吸附能和体积模量通常偏大。

2、计算吸附能时偏高，计算扩散能垒时偏低。

3、计算电子动量和角动量时偏低。

4、计算能带带宽时，偏低超过50%，有时甚至根本得不到能带带宽。

5、对于过渡态金属的计算不准确，因为这些金属核外电子密度变化剧烈。例如利用LDA计算Fe(铁磁性)和Cr(反铁磁性)两种物质时，最终得到的结果都是非磁性的。

6、对于有氢键和范德华力作用的体系的计算也不精确。

为了获得更精确的交换关联泛函，研究者们提出了广义梯度近似的交换关联泛函。

2. 广义梯度近似

在LDA方法中，交换关联泛函仅为电子密度的函数，而在GGA近似方法中，交换关联泛函是电子密度和电子密度梯度的函数。

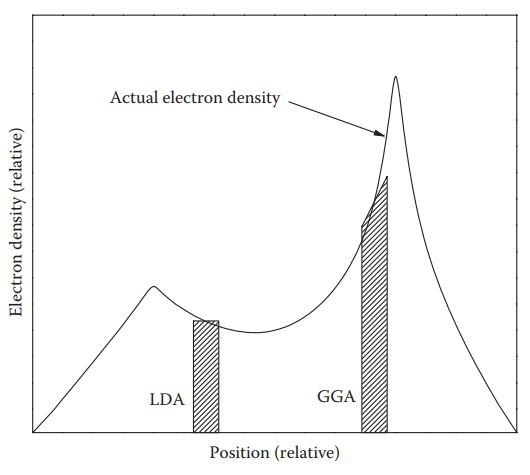
(交换关联泛函LDA和GGA的对比)

GGA形式的交换关联能可以表达为：

考虑自旋形式的交换关联能的表达式为：

在实际应用中，GGA的表达式其实是直接在LDA的表达式中增加一项与电子密度梯度有关的函数，如下式所示：

其中：

通常s的取值范围为0~3，而F(s)的取值范围为1~1.6。关于F的表达式有许多形式的GGA交换关联泛函，其中比较流行的有PW91和PBE两种类型，分别是Perdew和Wang 1992年和Perdew 1996年提出来的。其中PBE是改进的PW91版本的交换关联泛函，也是目前使用最广泛的，兼顾精度与效率的泛函。下面是利用PBE计算常见材料额晶格常数和体积模量。

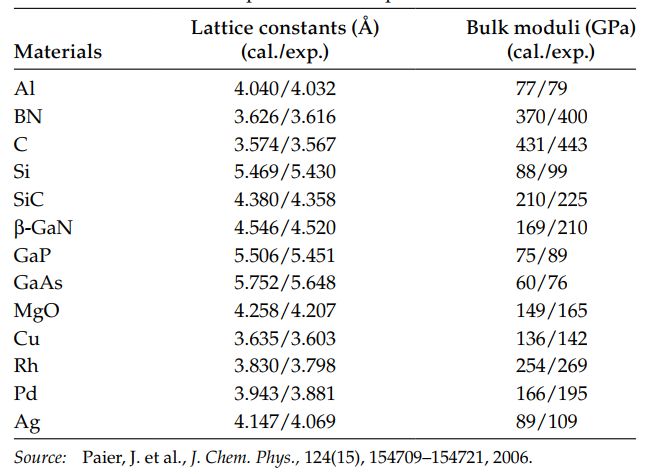
GGA几乎使用于所有的系统，对于结构参数的误差通常为1~3%。但是GGA在计算能带带宽的时候，仍然小于实际值超过50%。造成能带带宽估计偏小的原因有两个：首先，在Kohn-Sham方法中，计算带宽的方法与定义有出入，带宽的定义为：

而在Kohn-Sham方法中计算的带宽其实是：

在Kohn-Sham方法中并没有真实的增加或去除电子，所以更高能级n+1轨道的能量也是由n个电子估计的，因此能带带宽偏小。

第二个原因是源于交换关联泛函的连续性，而真实的交换关联泛函应该是不连续的。最终导致同一轨道上相同自旋的电子相互作用不能完全被排除，这就导致了共价带能量的升高，导带能量的降低，所以能带带宽就降低了。在H-F方法中，电子的关联效应可以有Slater行列式完全消除，因此由H-F方法计算的能带带宽通常偏大。

校正能带带宽计算的方法大致有三种：

1、使用混合H-F方法的交换关联泛函，

2、将能量用格林函数表述，利用多体摄动理论校正关联项；

3、使用其他关联项校正的方法。

在实际的DFT计算中，关联密度泛函往往是合并在赝势函数中的，在选择赝势的时候也就选择了交换关联泛函。

Kohn-Sham方程的求解

求解K-S方程通常采用自恰迭代法，如下图所示：

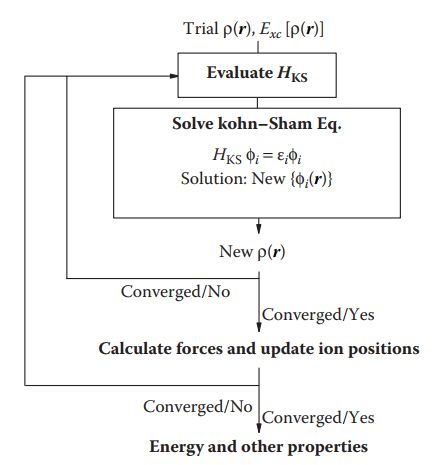
用于初始迭代的波函数是稍微多于n/2个的平面波以及由赝势函数提供的独立的原子周围的电子密度，然后不断代入K-S方程进行迭代，直到能量收敛至基态，达到停止的判断标准，通常为10^-5~10^-4 eV.

分子模拟交流学习，请扫码关注