r语言集合补集_【必修一】高中数学必备知识点：8.补集及综合应用

全集 全集的定义及表示

(1)定义：如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集．

(2)符号表示：全集通常记作U.

疑难解析：

对全集概念的理解

“全集”是一个相对的概念，并不是固定不变的，它是依据具体的问题来加以选择的．例如：我们常把实数集R看作全集，而当我们在整数范围内研究问题时，就把整数集Z看作全集.

补集

补集的概念和性质

疑难解析

理解补集应关注三点

(1)补集既是集合之间的一种关系，同时也是集合之间的一种运算．求集合A的补集的前提是A是全集U的子集，随着所选全集的不同，得到的补集也是不同的，因此，它们是互相依存、不可分割的两个概念．

(2)∁UA包含三层意思：①A⊆U；②∁UA是一个集合，且∁UA⊆U；③∁UA是由U中所有不属于A的元素构成的集合．

(3)若x∈U，则x∈A或x∈∁UA，二者必居其一．

补集运算

[例1]　(1)(广东高考)已知全集U＝R，A＝{x|x≤0}，B＝{x|x≥1}，则集合∁U(A∪B)＝ (　　)

A．{x|x≥0}　　　B．{x|x≤1}

C．{x|0≤x≤1}       D．{x|0＜x＜1}

(2)设U＝{x|－5≤x

[解析]　

(1)A∪B＝{x|x≤0，或x≥1}，

所以∁U(A∪B)＝{x|0

(2)法一：在集合U中，

∵x∈Z，

则x的值为－5，－4，－3,3,4,5，

∴U＝{－5，－4，－3,3,4,5}．

又∵A＝{x|x2－2x－15＝0}＝{－3,5}，

∴∁UA＝{－5，－4,3,4}，∁UB＝{－5，－4,5}．

求补集的方法

求给定集合A的补集通常利用补集的定义去求，从全集U中去掉属于集合A的元素后，由所有剩下的元素组成的集合即为A的补集．

例题：已知全集U，集合A＝{1,3,5,7}，∁UA＝{2,4,6}，∁UB＝{1,4,6}，求集合B.

解：∵A＝{1,3,5,7}，∁UA＝{2,4,6}，

∴U＝{1,2,3,4,5,6,7}．又∵∁UB＝{1,4,6}，

∴B＝{2,3,5,7}.

集合的交、并、补综合运算

解题技巧

解决集合交、并、补运算的技巧

(1)如果所给集合是有限集，则先把集合中的元素一一列举出来，然后结合交集、并集、补集的定义来求解．在解答过程中常常借助于Venn图来求解．这样处理起来，相对来说比较直观、形象且解答时不易出错．

(2)如果所给集合是无限集，则常借助数轴，把已知集合及全集分别表示在数轴上，然后进行交、并、补集的运算．解答过程中要注意边界问题．

练习：

已知全集U＝{x|x<10，x∈N*}，A＝{2,4,5,8}，B＝{1,3,5,8}，求

∁U(A∪B)，∁U(A∩B)，(∁UA)∩(∁UB)，(∁UA)∪(∁UB)．

解：∵A∪B＝{1,2,3,4,5,8}，

U＝{1,2,3,4,5,6,7,8,9}，

∴∁U(A∪B)＝{6,7,9}．

∵A∩B＝{5,8}，

∴∁U(A∩B)＝{1,2,3,4,6,7,9}．

∵∁UA＝{1,3,6,7,9}，∁UB＝{2,4,6,7,9}，

∴(∁UA)∩(∁UB)＝{6,7,9}，

(∁UA)∪(∁UB)＝{1,2,3,4,6,7,9}．

说明：作出Venn图，如图所示，由图形也可以直接观察出来结果．

补集的综合应用

解题技巧

利用补集求参数应注意两点

(1)与集合的交、并、补运算有关的参数问题一般利用数轴求解，涉及集合间关系时不要忘掉空集的情形．

(2)不等式中的等号在补集中能否取到，要引起重视，还要注意补集是全集的子集．

练习题：

已知集合A＝{x|x0}．若A∩(∁RB)＝∅，求实数a的取值范围．

解：∵B＝{x|x0}，

∴∁RB＝{x|－1≤x≤0}，

因而要使A∩(∁RB)＝∅，结合数轴分析(如图)，

可得a≤－1.

即实数a的取值范围是{a|a≤－1}．

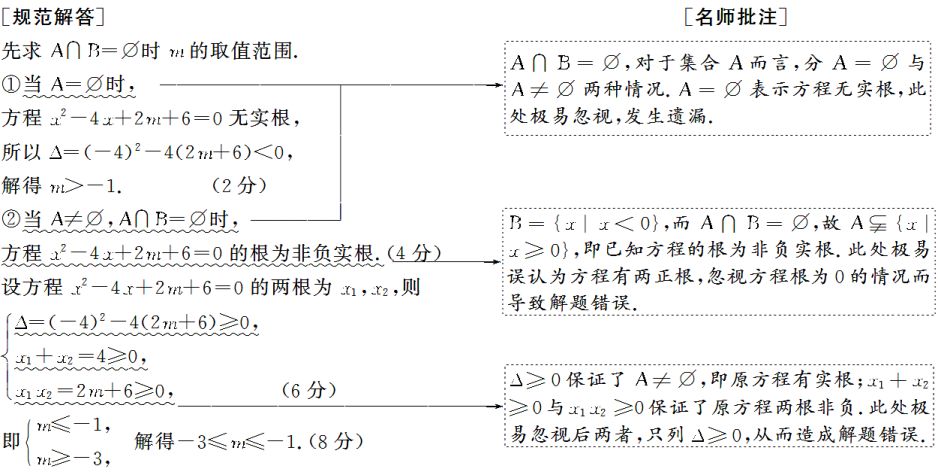
易错分析

1.补集思想的综合应用

[典例]　(12分)已知集合A＝{x|x2－4x＋2m＋6＝0}，B＝{x|x<0}，若A∩B≠∅，求实数m的取值范围．

解题流程

练习：

End

阅读推荐

1.20省高考分数线及一分一段表汇总！你目前的分数排全省多少名?

2.多省高考分数线公布！另附志愿填报完全版指南，一分也不允许你浪费！

3.高考成绩出来了，请不要打扰别人的幸福

4.一份超实用的志愿填报攻略，待查收！

▐ 来源：本文综合来源于网络，如有侵权请联系删除！

▐ 标签：高考地理  备战高考    知识汇总

▐ 更多内容请关注微信公众号平台：高考数学ID：gkdl100

点击“阅读原文”，做学霸