分数乘混合运算50道_5分钟看懂：怎么找单位“1”、分数乘法应用题各类题型解题思路...

人教版六年级上册第一单元 分数乘法的计算与分数乘法应用题各类题型解题思路专题总结

一、分数乘法计算

(一)分数乘法的意义：

1、分数乘整数与整数乘法的意义相同。都是求几个相同加数的和的简便运算。

例如：2/9×3表示求3个 2/9的和是多少？也表示2/9的 3 倍是多少？

3个 2/9的和是多少

2、分数乘分数是求一个数的几分之几是多少。

例如：1/2 × 1/4表示求1/2 的1/4是多少？

求1/2 的1/4是多少

(二)分数乘法的计算法则及注意事项：

1、分数与整数相乘：分子与整数相乘的积做分子，分母不变(整数和分母约分) 。

分数乘以整数的意义和计算方法

2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母(分子和分母约分)。

分数乘以分数的计算方法

3、分数与小数相乘：可以把小数化成分数，也可以把分数化成小数，也可以直接用分母与小数约分。

分数乘以小数的计算方法

4、为了计算简便，能约分的要先约分，再计算。

5、当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

6、分数连乘的计算方法：先约分，分子中可与分母约分的数都先约分，再用分子乘分子作积的分子，分母乘分母作积的分母。

7、分数的计算结果一定要保留最简分数。

(三)、乘积的变化规律(乘法中比较大小时)：

一个数(0 除外)乘大于1的数(大于1的假分数)，积大于这个数本身。

一个数(0 除外)乘小于1的数(0 除外，真分数)，积小于这个数本身。

一个数(0 除外)乘1，积等于这个数本身。

一个数(0 除外)乘0，积等于0.

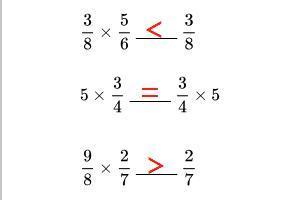
(四)、分数混合运算的运算顺序和整数的运算顺序相同。

同级混合运算(只有加减法或者只有乘除法)，按照从左到右的顺序依次计算；

两级混合运算(既有乘除法，又有加减法)，先算乘除、后算加减；

有小括号的时候，先算小括号里面的加减法，再算乘除法，后算括号外面的；

既有小括号又有中括号，先算中括号里面的小括号，再算中括号，最后算中括号外面。

(五)、整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律： a × b = b × a

乘法结合律： ( a × b )×c = a × ( b × c )

乘法分配律： ( a + b )×c = a c + b c 或 a c + b c = ( a + b )×c

二、分数乘法应用题(已知单位“1”的量用乘法，即求单位“1”的几分之几是多少)

1、找单位“1”： 一般分率句中分率的前面，或者“占”、“是”、“比”的后面，就是单位“1”的量。

2、画线段图帮助理解：

(1)、两个量的关系：画两条线段图，先画单位“1”的量，再画比较量；

(2)、部分和整体的关系：画一条线段图，先画整体，再画部分。

3、分数乘法应用题的基本类型：

(1)、求一个数的几分之几是多少： 一个数 × 几分之几【单位“1” × 分率】；

例题：求一个数的几分之几是多少

(2)、连续求一个数的几分之几是多少：一个数 × 几分之几 × 几分之几【单位“1” × 分率 × 分率】

例题2：连续求一个数的几分之几是多少

(3)、求比一个数多(或少)几分之几的数是多少：一个数 × (1+几分之几)或 一个数 × (1-几分之几) 【单位“1”× (1+(或-)分率)】

例3求比一个数多(少)几分之几的数

小技巧：

分率前是“的”： 单位“1”×分率=对应的量

分率前是“多或少”： 单位“1”×(1+分率)=对应的量

总结：分数乘法应用题其实并不难，找准单位“1”、找到要求的量以及这个量所对应的分率即可。

分数乘法和分数除法应用题，包括六年级上下册都会学到的百分数应用题，一定要把“量率对应”思想理解到位。