实现线段切割法_这道三年级奥数题，解题关键在“切割”上，来看看是怎么切割的...

三年级数学老师，为了使小学生的思维更加有深度，于是给小学生写了一道难度大点的奥数题，这道题的解题关键在“切割”上，来看看是怎么切割的吧!

如图:

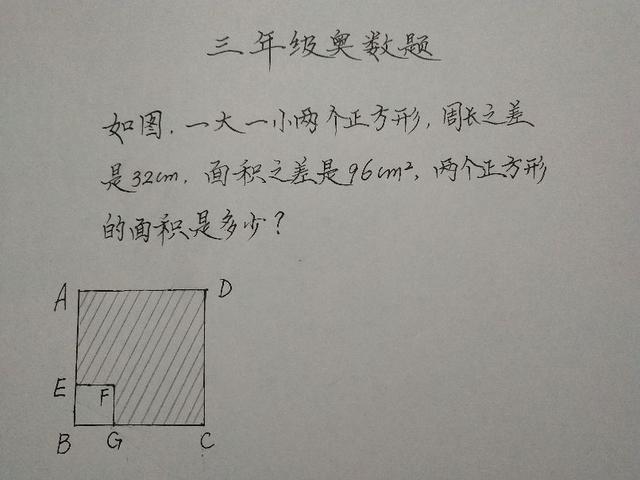
解题分析:

由题意可知是一大一小两个正方形，那么这两个正方形的每条边各是相等的。

因为两个正方形周长之差是32cm，所小正方形的每条边，都比大正方形的每条边长少:

32÷4＝8cm

8cm其实也就是线段AE、GC的长度，即AE=8cm，GC=8cm

接下来就是作辅助线来帮助小学生理解了:

根据题意可知:两个正方形的面积之差是96平方厘米，即上图中的阴影部分的面积是96平方厘米。

下面采取“切割法”把图中的阴影部分的面积，切割成三部分，这也是这道题的解题关键，具体做法是:

由“线段EF”延长至“M点”，由“线段GF”延长至“N”。

如图所示:

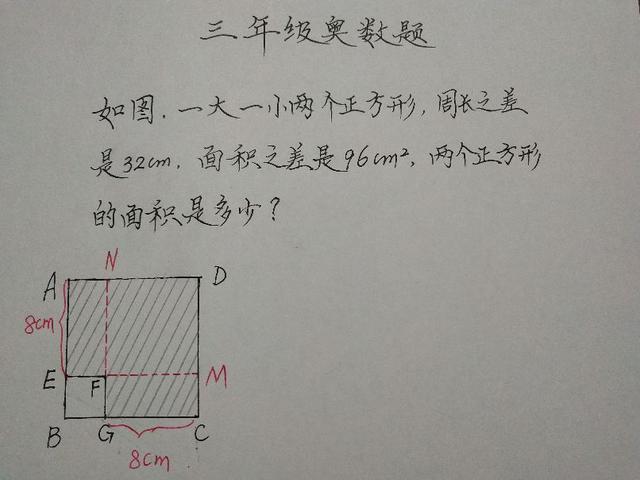
根据图示可直观地看出:

图形FMDN是正方形，它的边长就是线段AE的长度，即8cm，那么根据这个条件，就可以求出正方形FMDN的面积，即:

8×8＝64㎝²

那么再根据图中阴影部分的面积是96㎝²，可以求出剩下的阴影部分的面积，即:

96－64＝32㎝²

根据图示也可看出:

“图形AEFN”和“图形GCMF”是完全相同的两个长方形，也就是这两个长方形的面积相同。

看到这儿，小学生可能也发现了:

这两个长方形的面积，其实就是刚刚上面求出的剩下的阴影部分的面积，即:32㎝²，根据这些可以求出其中一个长方形(长方形AEFN)的面积是:

32÷2＝16㎝²

又知道这个长方形的一条边长:

AE=8cm

所以另外一条边长(也就是小正方形的边长)为:

16÷8=2㎝

那么小正方形的面积为:

2×2=4㎝²

再根据:AE=8㎝，BE=2㎝，可以求出大正方形边长，即AE的长为:

8+2＝10㎝

所以大正方形的面积为:

10×10=100㎝²

计算如图:

这是道相当有难度的经典题，做这道题的关键在于对阴影部分的切割，也就是作的辅助线。

家有小学生的朋友们，可以让孩子做一做，看看能想到这种“切割法”吗？

如果你有不同的解题方法，欢迎留言探讨哦！

点击关注，随时学习，请@专注分享小学思维拓展题的虎妈猫师。