关于坐标变换的总结

2019独角兽企业重金招聘Python工程师标准>>>

约定本文的向量均以行向量来表达，就记向量为V吧。

我们直截了当学习构造一个代表运动的矩阵吧。构造的结果是一个矩阵M，这个矩阵代表一个运动。求得M之后，用V*M就代表对向量V执行M代表的运动，即算出向量V在执行M代表的运动之后，具备的新坐标V'。这个所谓的新坐标V'，与旧坐标V处于同一坐标系。因此，准确的说，我这儿所说的运动，是指在一个坐标空间中，将物体从一个地方搬到另一个地方，这两个地方的地址描述都是在同一个坐标空间的参照下。物体的老地址（老坐标）是V，搬动之后，新地址（新坐标）是V'。那么，我所要构造的矩阵M，其实描述的就是这个搬动动作--怎么个搬动法，或者你也可以认为M描述的是新旧坐标之间的一种【一一映射】关系。强调一下，这里的搬动只是比较直观的表述，实际上我要说的是运动，包括旋转。

搞明白了上面这些，我们就对运动的描述（用矩阵描述）与运动的执行（用乘法来执行）以及运动的结果（将物体搬到了新地方，得到了新坐标）有了一点点总体的印象。然后，我再来说怎么构造这样一个代表运动的矩阵。首先，我们先看3*3单位矩阵，由于我约定向量为行向量，因此，矩阵的每一行都是一个坐标基，即单位坐标轴的坐标，比如第一行为(1 0 0)，第二行为(0 1 0)，第三行为(0 0 1)。关键的地方来了，假设我们把物体绕X轴旋转θ角，那么我们所需要的描述这个旋转动作的矩阵M，其每一行的坐标基，就是单位坐标基分别都做这个旋转动作后具备的新坐标。即：老x坐标基（1 0 0）旋转后成为新x坐标基（1 0 0），老y坐标基（0 1 0）旋转后成为新y坐标基（0 cosθ sinθ），老z坐标基（0 0 1）旋转后成为新z坐标基（0 -sinθ cosθ），最终，矩阵M的三行分别就是这三个新坐标基：

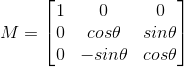
这就是要求的变换矩阵。总结一下就是，变换矩阵的三行，就是单位矩阵的坐标基分别变换后的新坐标。这就是构造变换矩阵的方法。这里的变换，可以是旋转，可以是缩放，也可以是镜像，切变等等（这里不包含投影变换），但求变换矩阵的方法都是一样的。

平移变换需要单独讲一下。平移变换是个最简单的变换，但是却不能按照上述的方法来构造。上面的变换只能描述线性变换，但平移变换不是线性变换，而是所谓的仿射变换。构造平移变换的方法极其简单：在3*3单位矩阵的三行坐标基下面再加一行，我称其为【平移基】。比如：向x轴、y轴、z轴分别平移1、-1、2个单位，则平移基为(1 -1 2)，最终的平移变换矩阵就是：

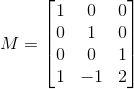
这个矩阵不能合法的与三维向量相乘，因此，这里又要引入四维齐次坐标的概念：将3D向量增加一个分量，变成4D向量，将4*3矩阵增加一列，变成4*4矩阵。这里稍微讲一下齐次坐标相关的东西：3D向量本身既可以用来描述点的坐标，也可以用来描述矢量，但矢量是没有平移的概念的，所以当3D向量表示的是矢量时，我们给该3D向量增加的分量是0，这样它与M相乘时，平移基会被增加的这个0给乘成0，即平移基不会起作用。当3D向量表示的是点时，我们增加的分量是1，这样它与M相乘时，平移基会作用在向量的每个分量上，起到平移的效果。矩阵增加的一列是.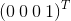

这样，综合一下，变换矩阵M是一个4*4矩阵，前三行是坐标基，第四行是平移基。构造这样一个变换矩阵的方法是：线性变换的部分，将单位矩阵的三个坐标基分别进行同样的线性变换，得到新的坐标基，作为矩阵的前三行；平移变换的部分，直接填数到平移基即可。最终所得即为所求。顺便提一下，我们约定的向量是行向量，对应有，矩阵的每一行是坐标基或平移基；若约定向量为列向量，则矩阵的每一列是坐标基或平移基。记住了这一点，则向量与矩阵相乘时，哪个在左边哪个在右边就绝不会搞错了。

上面罗里吧嗦的讲了一大堆，其实核心就一条：如何构造一个变换矩阵。而且，构造的是物体变换矩阵。即坐标系不变，将物体进行变换，得到其新的坐标。你可以指定一个点，与M相乘，看看得到的结果与你将这个点进行相应的变换后，是不是同一个结果。肯定是。同时，我们也知道，变换物体与变换坐标系其实是反向等价的。那么，其实我们现在也就知道如何构造坐标系变换矩阵了。在数学上，就是将4*4的物体变换矩阵左上角的3*3子矩阵进行转置，将第四行的平移基进行取反，所得即所求。这里解释一下：因为3*3子矩阵是整个变换的线性变换部分，是可逆的，其逆矩阵等于其转置矩阵。在不同的3D软件系统之间，往往就涉及到坐标系变换的问题。我想留到最后来专门讲一下这个坐标系变换的问题。

到这里为止，单次的变换，我们可以求得其对应的矩阵表示了。那么若干次的变换序列，是个什么情况呢？

不要闭着眼睛直接回答：不就是矩阵连乘么！这里面是有个思维路线过程的，“矩阵连乘”这四个字在没有明确一些重要前提条件的情况下，显得比较空洞和无法实用。正确的思维过程是这样的：首先还是回到我们上面的构造过程，构造过程中有个很重要的前提，坐标系是没有变化的。是这个坐标系里的物体在变换。我们构造的矩阵也是个物体变换矩阵。对坐标系里的物体执行变换的过程，就是用V*M来进行。得到的结果是物体的新坐标--同一个坐标系里的新坐标V'。在这整个过程再来一遍时，和第一遍没什么太大的不同，唯一的区别是物体在新的地方重复这个变换过程。其他的意义都没有发生变化。因此会得到一个更新的坐标V''而已，且V''=V' * M。只有讲出了这个模式时，接下来的第三遍、……第N遍，才会真实而明确：(((V * M) * M) * M) * M……根据结合律，括号可以都去掉，也可以将所有的M都括到一起，于是M' = M * M * …… ，变换结束时，V' = V * M'。这个思维路程中，可以清晰的看到这么一个道理：多个变换其效果等于一个变换。这才是“矩阵连乘”这四个字的内涵。走了这么一个过程，我们也就知道了为何可以连乘，以及实际使用时该如何做才是正确的。

其实这些都不复杂，可以说很简单，但在实际项目使用这些理论时，还是经常会碰到一些混乱。在我的实际经验中，混乱与错误，一般是由于没有搞清楚到底该构造物体变换还是该构造坐标系变换造成的，尤其是有些需求中既有物体变换又有坐标系变换。这个是需要根据项目实际情况来判断的，犯错误的次数多了，多总结总结，自然就会少犯错，甚至养成正确的直觉。建议大家先把构造物体变换矩阵的方法多实践练习几次，达到熟练掌握的程度。在我的理论中，这个是根基。把这个根基牢牢把握住了，后面的变换知识水到渠成。

以上是基础知识，比较没有歧义，可以命名为第一部分。接下来想讲一些容易混淆的问题，就叫做第二部分吧。

首当其冲的就是“欧拉角”。混乱是从这个问题中产生的：如何将欧拉角转换为四元数或矩阵？我们以转换为矩阵为例来讲。有了第一部分的理论，我们转换的思路应该是有的，欧拉角嘛，就3个角，看成3次变换，一次变换就是绕一个轴转动一个角度。自然地，我们得出变换矩阵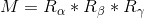。其实我认为这就是对的，没有问题，只要它满足我们构造矩阵的前提。但问题是，在实际项目中，有些时候这个前提并不满足。因为欧拉角在一种归类法上，可以分成两大类：内在的和外在的，英文中叫intrinsic和extrinsic。所谓的内在外在，是说：物体自身是有自己的坐标系的，这个坐标系是长在物体身上的，那么当物体转动时，这个坐标系也会转动，如果欧拉角的3个角度，都是描述的物体绕自身这个坐标系的轴的转动，那么这个欧拉角就叫做内在的欧拉角。如果欧拉角的3个角度，都是描述的物体绕体外不变的坐标系的轴的转动，那么这个欧拉角就叫做外在的欧拉角。我就呵呵了。既然说到这儿，就顺便提一下，欧拉角通常有这样一种分类法，a-b-a或者a-b-c，前者意思是欧拉角的第三次旋转的旋转轴与第一次的一样，后者的意思是欧拉角的三次旋转分别绕不同的坐标轴。这样，xyz三个轴，总共有12种欧拉角。再加上刚说的内在与外在之分，总共就有24种欧拉角。正是这种多姿多彩，导致了在不同软件系统之间进行坐标变换时，欧拉角会带来巨大麻烦，是个真正的麻烦制造者，我一般称其为rubbish。那么回到我们刚才的话题，欧拉角转矩阵，按照我们第一部分的要求，构造变换矩阵时，始终是在同一个坐标系之中，因此，当欧拉角是外在的欧拉角时，我们的“矩阵连乘”法正是满足要求的。那么，当欧拉角是内在的时，我们能求出对应的变换矩阵吗？答案是肯定的。其实问题的核心还是要真正理解“矩阵连乘”法则。连乘法则的重要前提是各个变换都是在同一个坐标系下描述的，反之，也成立！即：当变换是在同一个坐标系下描述的时候，这些变换的序列其效果等价于一个“矩阵连乘”结果。因此，不管欧拉角的三次变换是怎么变的，我们真正要做的事情，就是在一个统一的坐标系里描述所有的变换。不止是欧拉角的例子，任何类似的变换问题，我觉得都应该这么想一想。拿具体例子来说事吧。假设有一个外在的欧拉角α−β−γ，它的三次变换所对应的变换矩阵分别是Rα−Rβ−Rγ，这三个变换矩阵很明显都是在【外在系】里的变换描述，因此这三个变换的序列等效于一个变换：Rα * Rβ * Rγ。这里我必须直接给出一个结论，在后面再证明它--外在的欧拉角α−β−γ等价于内在的欧拉角γ−β−α。根据这个结论，情况就很简单了：当给出的是外在的欧拉角时，用本文第一部分的方法按照欧拉角定义的顺序依次构造三个变换矩阵之后直接连乘得出欧拉角对应的变换矩阵；当给出的是内在的欧拉角时，用本文第一部分的方法按照欧拉角定义的顺序逆序构造三个变换矩阵之后直接连乘得出欧拉角对应的变换矩阵。所以，其实“矩阵连乘”本身是没啥混淆的地方，关键是能否抓住规则适用的前提条件。现在来看看内在外在欧拉角的逆序等价性的证明吧。这个网上能找到很多证明，我放一个证明链接到这儿，自己去看吧。证明里值得注意的一点是：内在欧拉角的三个旋转Eγ-Eβ-Eα，也是在【外在系】里的变换描述。即：不管是内在的还是外在的欧拉角，我们要构造的变换矩阵都是在【外在系】里的描述，构造方法如第一部分所述。

在实际项目中面临坐标变换问题时，大致还是可以从两个层次来着手的。首先，根据需求把理论捋顺，要构造什么，怎么构造，上面都有现成的理论可以照着做。然后，考虑具体的软件系统中，每个概念对应什么程序对象，api规范，期待的有效数据等等。在这后一个层次中，有一点值得一提，就是使用第三方的线性代数库，比如Eigen库等等。一般来说，线性代数库是纯粹的数学运算库，应用范围广泛，不是专为图形学变换定制的，因此没有所谓的左右手系规定、行列向量之分等等。当然，Eigen库里有提到Matrix是列向量存储的，但在逻辑意义上是没有行列之分的。数学运算库只是做数值计算，它真的不关心我们所谓的左右手系规定等等，它所做的工作就是纯粹按照数学规则，将我们输入给它的数值处理后返回给我们。比如，我们需要一个绕x轴旋转θ角的变换，那么eigen库可能就会直接返回给我们下面这个矩阵：

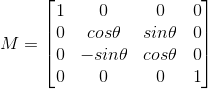
那么这么一个变换矩阵，当我们是x轴指向屏幕里面的右手系时，它是代表顺时针旋转θ角，当我们是x轴指向屏幕里面的左手系时，它是代表逆时针旋转θ角。但是这两种情况都满足我们事先告诉eigen要做的事--构造一个绕x轴转θ角的变换，这个结果也正是处在一种确定坐标手性的我们所需要的，因为只有我自己知道我处在什么坐标手性、坐标轴的指向，我知道我在右手系，知道我的x轴指向屏幕里面，那我理所应当的应该知道绕x轴转θ角的变换是顺时针旋转，所以eigen返回的结果符合我的预期。当我处在左手系，x轴指向屏幕里时，我也理所应当的知道绕x轴转θ角的变换应该是逆时针旋转，eigen返回的结果还是符合我的预期。当我处在x轴指向屏幕里面的右手系时，如果我想eigen帮我构造一个逆时针转θ角的变换，那我传参数的时候，自己就应该知道要传-θ，而不是之前的θ，此种情况eigen自然会返回一个不同的矩阵。也就是说，矩阵的意义是我们赋予的，矩阵的16个数字是eigen填写的，但它填的很正确，满足我们的预期。

最后，让我们着手解决第一部分留下的一个重要问题：不同3D系统之间的坐标系变换。

首先排除欧拉角！不要挑战自己。不同3D系统之间，直接将欧拉角进行变换，完全是自找不痛快。因为上面我们说了，通常欧拉角就有24种之多，再加上不同3D系统里可能对欧拉角还有自己的各种奇葩设定，令人防不胜防。比如设定欧拉角的范围是0~65535,0~360等等等等，别问我碰到过这种奇葩没有，说出来都是泪。

排除欧拉角之后，我们来说说矩阵。这里有两个坐标系：源坐标系、目的坐标系。我们能提供的数据是源坐标系里物体的坐标，因此，正常情况下能构造从源坐标系到目的坐标系的物体变换矩阵。不过，真实的情况是，物体本身在空间中并没有运动，我们只是想要知道这个物体在目的坐标系里的坐标是什么。因此，这是一个坐标系变换问题，我们只需要把构造的源坐标系到目的坐标系的物体变换矩阵求逆即为所求。这里的难点可能在于找到一个变换序列，不过也算不上什么难点，随便找一条变换路径，总是能构造出来的。值得欣慰的是，一般现实中的不同3D系统的坐标系之间，有坐标轴互相平行。这个就很简单了，按照我们的构造方法，只需要把坐标基交换顺序改改符号就可以构造出了，平移基单独仔细处理一下，不会是问题。

再说说四元数。四元数只是表达旋转的，所以平移得单独处理。四元数的跨3D系统坐标变换，核心是脑子里要有一幅画面：一根旋转的弓箭，即所谓的轴角对。这根旋转的弓箭，在源坐标系与目的坐标系中一致，它就在空间中那么的转，我们要做的只不过是在不同的坐标系中用不同的四元数来描述同一个事物。有两个方法可以构造这个四元数。其一，利用系统自带或第三方数学库，若两个坐标系手性相反，则将源坐标系反掉一根轴，然后对四元数求逆，然后随便构造一个四元数序列，将反调轴之后的坐标系与目的坐标系运动对齐，所有这些四元数连乘，就是所要的变换四元数。若两个坐标系手性相同，则直接构造一个四元数序列，将源坐标系与目的坐标系的坐标轴运动对齐，所有四元数连乘即为所求。其二，伸出双手比划比划，就可以很直接的写出最终变换四元数了，标准是同样的旋转，在不同坐标系符号一致的话，则数值保持同号，符号不一致的话，则数值反号。这里写的比较简略，自己总结吧。

=============2017.08.16-23:44 补充 ↓ ===============

关于三个坐标轴分别平行的坐标系之间的坐标系变换矩阵的求法，稍微详细说一下：

还是按照最开始说的，先求物体变换矩阵。先写出目的坐标系的x、y、z轴单位方向向量在源坐标系里的坐标，这就是源坐标系的坐标基进行物体变换之后的新坐标基，因此这三个坐标直接就是所求的物体变换矩阵(在源坐标系里)。然后，将该物体变换矩阵求逆，就得到源坐标系到目的坐标系的坐标系变换矩阵。同时，我们也知道，源坐标系到目的坐标系的坐标系变换矩阵求逆，就得到目的坐标系到源坐标系的坐标系变换矩阵，所以，源到目的的物体变换矩阵就是目的到源的坐标系变换矩阵，也就是目的坐标系的坐标基在源坐标系里的坐标构成的矩阵，就是目的到源的坐标系变换矩阵。反过来也成立，源坐标系的坐标基在目的坐标系里的坐标描述，就是源坐标系到目的坐标系的坐标系变换矩阵。

=============2017.08.17-10:53 补充 ↓ ===============

刚才审视昨晚补充的内容，有点搞笑。其实上面得出的结论【源坐标系的坐标基在目标坐标系里的坐标描述，就是源坐标系到目标坐标系的坐标系变换矩阵】是通用的，不管两个坐标系的轴是否平行。只不过坐标轴平行的情况下，一个坐标系的坐标基在另一个坐标系里的描述可以很轻松的直接看出来。

=============2018.06.06-14:37  ↓ ===============

建立坐标系，一定是指在一个已有的坐标系里建立一个新坐标系，首先就得搞清楚这一点。那么，怎么才叫建立了这个坐标系呢？那就是在已有的那个坐标系里描述清楚了新坐标系的原点和旋转。

转载于:https://my.oschina.net/zhoubaojing/blog/894512