GMM高斯混合模型学习笔记（EM算法求解）

  提出混合模型主要是为了能更好地近似一些较复杂的样本分布，通过不断添加component个数，能够随意地逼近不论什么连续的概率分布。所以我们觉得不论什么样本分布都能够用混合模型来建模。由于高斯函数具有一些非常有用的性质。所以高斯混合模型被广泛地使用。

    GMM与kmeans相似，也是属于clustering，不同的是。kmeans是把每一个样本点聚到当中一个cluster，而GMM是给出这些样本点到每一个cluster的概率。每一个component就是一个聚类中心。

    GMM(Gaussian Mixture Model)高斯混合模型，由K个不同的Gaussian线性组合而成，每一个Gaussian是混合模型的一个component，GMM的概率密度函数例如以下： 

p(x)=∑k=1Kp(k)(x|k)=∑k=1Kπk(x|μk,∑k)

    依据上式。从GMM中生成一个样本点x分两步： 
    1，从K个component中随机的选择一个 
    2。从该component中选择一个点

    參数说明：N个样本点。K个component，μk,∑k 是第k个component的均值和协方差矩阵，是模型參数，是须要预计的。

πk是mixing coefficient，表示第k个component被选中的概率。πk=1N∑Nn=1znk，也是模型參数。须要预计。N是高斯（正态）分布。

    对一个样本集建立高斯混合模型的过程，就是依据已知样本集X反推高斯混合模型的參数(μ,∑,π)，这是一个參数预计问题。首先想到用最大似然的方法求解，也就是，要确定參数π,μ,∑使得它所确定的概率分布生成这些样本点的概率最大。这个概率也就是似然函数，例如以下： 

p(x)=∏n=1Np(xi)

而一般对于单个样本点其概率较小。多个相乘后更小，easy造成浮点数下溢，所以通常是对似然函数求log，变成加和形式： 

∑i=1Nlnp(xi)

    这个叫做log似然函数，目标是要最大化它。用log似然函数对參数分别求偏导。令偏导等于0，可求解得參数。 
    然而。GMM的log似然函数是例如以下形式： 

lnp(X)=∑i=1Nln[∑k=1Kπk(xi|μk,∑k)]

    能够看到对数中有求和，直接求导求解将导致一系列复杂的运算，故考虑使用EM算法。（详细思路见上一篇： EM算法学习笔记 ）

    考虑GMM生成一个样本点的过程，这里对每一个xi引入隐变量z，z是一个K维向量，如果生成xi时选择了第k个component，则zk=1，其它元素都为0。∑Kk=1zk=1. 
    如果z是已知的。则样本集变成了{X,Z}，要求解的似然函数变成了： 

p(X,Z|μ,∑,π)=∏n=1N∏k=1Kπznkk(xn|μk,∑k)znk

log似然函数为： 

lnp(X,Z|μ,∑,π)=∑n=1N∑k=1Kznk[lnπk+ln(xn|μk,∑k)].(∗)

    能够看到，这次ln直接对Gaussian作用，求和在ln外面，所以能够直接求最大似然解了。

1,初始化一组模型參数π,μ,∑ 
2,E-step

---

    然而。其实z是不知道的。我们仅仅是如果z已知。

而z的值是通过后验概率观測。所以这里考虑用z值的期望在上述似然函数中取代z。 
    对于一个样本点x： 

p(z)=∏k=1Kπzkk

p(x|zk=1)=(x|μk,∑k)

p(x|z)=∏k=1K(x|μk,∑k)zk

p(x)=∑zp(z)p(x|z)=∑k=1Kπk(x|μk,∑k)

    后验概率（固定 μ,∑,π ）： 

p(z|x,μ,∑,π)=p(x|z)p(z)p(x)正比于∏n=1N∏k=1K[πk(xn|μk,∑k)]znk

    由于{ zn }之间是相互独立的。 
    计算z期望 γ(znk) （z向量仅仅有一个值取1，其余为0）： 

γ(znk)=E[znk]=0∗p(znk=0|xn)+1∗p(znk=1|xn)=p(znk=1|xn)=p(znk=1)p(xn|znk=1)p(xn)=πk(x|μk,∑k)∑Kj=1πj(x|μj,∑j).

    将z值用期望取代。则待求解的log似然函数(*)式变为： 

Ez[lnp(X,Z|μ,∑,π)]=∑n=1N∑k=1Kγ(znk)[lnπk+ln(xn|μk,∑k)].

3,M-step

---

    如今能够最大化似然函数求解參数了，首先对μ求偏导，令偏导等于0。可得： 

∑n=1N∑k=1Kγ(znk)∑k(xn−μk)=0

μk=1Nk∑n=1Nγ(znk)xn，其中Nk=∑n=1Nγ(znk).

Nk  是“the effective number of points assigned to cluster k”. 
    再对 ∑k 求偏导，令偏导等于0，可得： 

∑k=1Nk∑n=1Nγ(znk)(xn−μk)(xn−μk)T

    接下来还需求解π。注意到π需满足∑Kk=1πk=1。所以这是一个带等式约束的最大值问题。使用拉格朗日乘数法。 
    构造拉格朗日函数： 

L=lnp(X|π,μ,∑)+λ(∑k=1Kπk−1).

    对 π 求导，令导数为0： 

∑n=1N(x|μk,∑k)∑Kj=1πj(x|μj,∑j)+λ=0

    两边同乘 πk 得： 

∑n=1Nγ(znk)+λπk=0

Nk+λπk=0

    两边对k求和： 

∑k=1KNk+∑k=1Kλπk=0

N+λ=0

    可得： λ=−N  
    代入可得： πk=NkN.

4,检查是否收敛 
    反复E-step和M-step两步。直到收敛，就可以求得一个局部最优解。

---

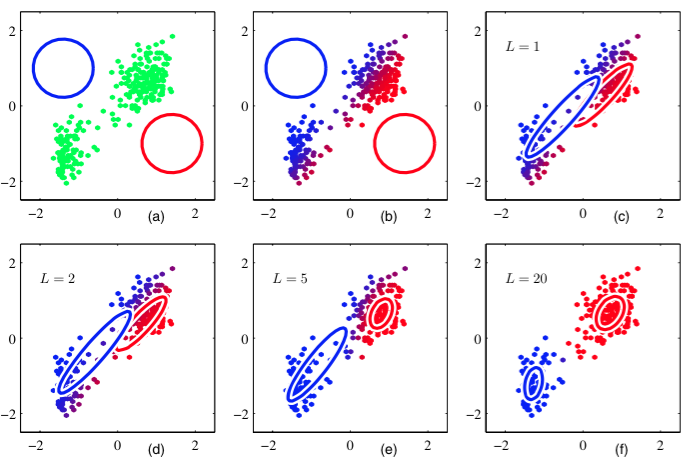
GMM的建模步骤例如以下图（k=2,高斯分布是蓝色和红色圈）： 

---

主要參考资料： 
《Pattern Recognization and Machine Learning》 
帮助理解： 
http://blog.pluskid.org/?p=39

本文转自mfrbuaa博客园博客，原文链接：http://www.cnblogs.com/mfrbuaa/p/5111355.html，如需转载请自行联系原作者