本节书摘来自华章出版社《深度学习导论及案例分析》一书中的第3章,第3.2节,作者李玉鑑 张婷,更多章节内容可以访问云栖社区“华章计算机”公众号查看。
3.2受限玻耳兹曼机的学习算法
受限玻耳兹曼机的学习就是对模型参数集θ进行计算,常用的方法是最大似然估计,其基本思想在于采用梯度上升算法最大化总体对数似然函数。在给定可视向量训练集S={v(l),1≤l≤N}时,受限玻耳兹曼机的对数似然函数定义为
lRBM(θ)=log∏Nl=1p(v(l)θ)=∑Nl=1logp(v(l)θ)(3.11)
由于
lRBM(θ)=∑Nl=1log∑hp(v(l),hθ)=∑Nl=1log∑hexp(-ε(v(l),hθ))∑v,hexp(-ε(v,hθ))
=∑Nl=1(log∑hexp(-ε(v(l),hθ))-log∑v,hexp(-ε(v,hθ)))(3.12)
所以,受限玻耳兹曼机的对数似然梯度为
lRBM(θ)θ=∑Nl=1θlog∑hexp{-ε(v(l),hθ)-log∑v,hexp{-ε(v,hθ)}
=∑Nl=1∑hexp(-ε(v(l),hθ))∑hexp(-ε(v(l),hθ))×(-ε(v(l),hθ))θ
-∑v,hexp(-ε(v,hθ))∑v,hexp(-ε(v,hθ))×(-ε(v,hθ))θ
=∑Nl=1-∑hp(hv(l),θ)(ε(v(l),hθ))θ+∑v,hp(v,hθ)(ε(v,hθ))θ
=∑Nl=1-Ep(hv(l),θ)(ε(v(l),hθ))θ+Ep(v,hθ)(ε(v,hθ))θ(3.13)
其中,Ep(•)表示求关于分布p的数学期望,p(hv(l),θ)表示在可视向量为v(l)时,隐含向量的条件概率分布。
根据公式(3.13)可得对数似然梯度关于各个参数的偏导为
lRBM(θ)wij=∑Nl=1(Ep(h|v(l),θ)[hiv(l)j]-Ep(v,h|θ)[hivj])
=∑Nl=1(p(hi=1|v(l),θ)v(l)j-∑vp(v|θ)p(hi=1|v,θ)vj)(3.14)
lRBM(θ)aj=∑Nl=1(EP(h|v(l),θ)[v(l)j]-Ep(v,h|θ)[vj])=∑Nl=1(v(l)j-∑vp(v|θ)vj)(3.15)
lRBM(θ)bi=∑Nl=1(Ep(h|v(l),θ)[hi]-Ep(v,h|θ)[hi])
=∑Nl=1(p(hi=1|v(l),θ)-∑vp(v|θ)p(hi=1|v,θ))(3.16)
显然,直接利用公式(3.14)~公式(3.16)计算上述偏导值的效率是非常低的,因为在计算Ep(v,h|θ)[hivj]、Ep(v,h|θ)[vj]和Ep(v,h|θ)[hi]的期望值时,需要进行具有指数复杂度的求和运算。
为了快速计算受限玻耳兹曼机的对数似然梯度,可以采用一类称为对比散度(Contrastive Divergence,CD)的近似算法[146,147]。其中常用的是k步对比散度算法(kstep Contrastive Divergence,CDk),详见算法3.1。注意,算法3.1并未加入学习率等预设参数,与网上下载的实现代码可能略有不同。
算法3.1k步对比散度(CD-k)
输入:RBM(v1,…,vm,h1,…,hn)、训练集S={v(l),1≤l≤N}
输出:梯度近似Δwij、Δaj、Δbi,其中,i=1,…,n,j=1,…,m
初始化:Δwij=Δaj=Δbi=0,其中,i=1,…,n,j=1,…,m
for all the v(l)∈S do
g(0)←v(l)
for t=0,…,k-1 do
for i=1,…,n do h(t)i~p(hig(t),θ) end for
for j=1,…,m do g(t+1)j~p(vjh(t),θ)end for
end for
for i=1,…,n,j=1,…,m do
Δwij←Δwij+p(hi=1g(0),θ)•g(0)j-p(hi=1g(k),θ)•g(k)j
end for
for j=1,…,m do Δaj←Δaj+(g(0)j-g(k)j) end for
for j=1,…,n do Δbj←Δbi+p(hi=1g(0),θ)-p(hi=1g(k),θ) end for
end for
不难看出,CDk算法的核心是一种特殊的吉布斯采样,称为交错吉布斯采样(alternating Gibbs sampling)或者分块吉布斯采样(blocked Gibbs sampling)[145],如图3.3所示。吉布斯采样是一种MCMC算法,在直接采样困难的情况下,可以用来生成一个吉布斯蒙特卡罗马尔可夫链或吉布斯链[148,149],用以近似一个给定多变量分布的样本。交错吉布斯采样主要包括下面两个关键步骤:
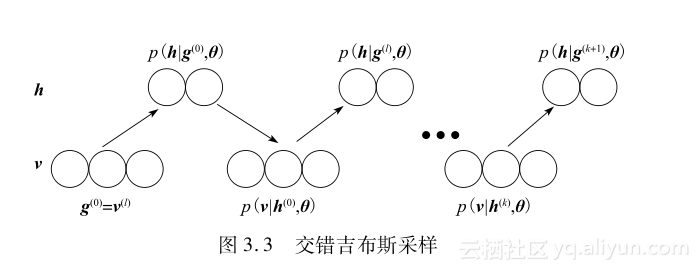
1)令t=0,用可视向量的训练样本v(l)初始化吉布斯链,得到g(t)=(g(t)1,g(t)2,…,g(t)m)T=v(l)。
2)通过迭代依次从p(hg(t),θ)采样h(t)=(h(t)1,h(t)2,…,h(t)n),从p(vh(t),θ)采样g(t+1),直到t+1=k。
对每一个可视向量样本v(l),都可以利用交错吉布斯采样生成一个k步吉布斯链,g(l,0)=v(l),h(l,0),g(l,1),…,h(l,k),g(l,k+1)。根据这个吉布斯链,就可以近似计算在训练样本仅为v(l)时的对数似然梯度如下:
lRBM(θ)wij≈∑Nl=1(p(hi=1g(l,0),θ)g(l,0)j-p(hi=1g(l,k),θ)g(l,k)j)(3.17)
lRBM(θ)aj≈∑Nl=1(g(l,0)j-g(l,k)j)(3.18)
lRBM(θ)bi≈∑Nl=1(p(hi=1g(l,0),θ)-p(hi=1g(l,k),
θ```
))(3.19)
显然,算法3.1就是公式(3.17)~公式(3.19)的结果。它被称为CDk是因为最大化RBM的对数似然函数lRBM(θ)在理论上恰好等价于最小化KullbackLeibler散度KL(p0p∞)=1NlogN-1N∑Nl=1logp(v(l)|θ),而在实践上又近似等价于最小化两个KullbackLeibler散度之差[62,64,146],即
CDk=KL(p0p∞)-KL(pkp∞)
=1NlogN-1N∑Nl=1logp(g(l,0)|θ)-1NlogN-1N∑Nl=1logp(g(l,k)|θ)
=1N∑Nl=1(logp(g(l,0)|θ)-logp(g(l,k)|θ))(3.20)
其中,p0(vθ)=1N∑Nl=1δ(v-v(l))=1N∑Nl=1δ(v-g(l,0))
是可视向量的经验分布,pk(vθ)=1N∑Nl=1δ(v-g(l,k))是在给定参数时,k步吉布斯链产生的重构分布,p∞(vθ)=p(vθ)则是平衡分布。
虽然CDk在计算受限玻耳兹曼机的对数似然梯度时是一种有偏的随机梯度方法,但其中的偏差会在k趋于∞时消失。在实际应用中,常常只需取k=1,就可以达到足够好的效果。目前,关于CDk算法的收敛性还没有得到严格的理论证明,对其合理性和收敛性的启发式分析可进一步参看文献[150,151]。
通过选择学习率η、权重退化率λ、动量加权率ν,还可以根据公式(3.21)迭代更新RBM的参数集θ,直到满足一定的收敛条件:θ(t+1)=θ(t)+ηlRBM(θ(t))θ-λθ(t)+νΔθ(t-1):=Δθ(t)(3.21)
最后应该指出,关于受限玻耳兹曼机的学习,还可以使用对比散度学习的改进算法,如持续对比散度(Persistent Contrastive Divergence,PCD)[152]和快速持续对比散度(Fast Persistent Contrastive Divergence,FPCD)[153],以及其他算法,包括并行回火(Parallel Tempering,PT)[154]、伪似然(pseudo likelihood)[155]、比率匹配(ratio matching)[156]等。



















 764
764











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








