图像处理之高斯一阶及二阶导数计算
图像的一阶与二阶导数计算在图像特征提取与边缘提取中十分重要。一阶与二阶导数的
作用,通常情况下:
一阶导数可以反应出图像灰度梯度的变化情况
二阶导数可以提取出图像的细节同时双响应图像梯度变化情况
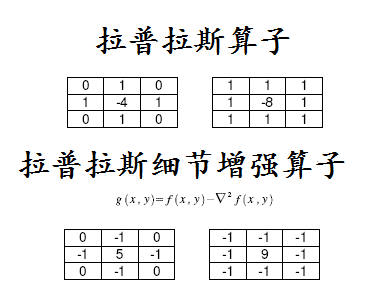
常见的算子有Robot, Sobel算子,二阶常见多数为拉普拉斯算子,如图所示:
对于一个1D的有限集合数据f(x) = {1…N}, 假设dx的间隔为1则一阶导数计算公式如下:
Df(x) = f(x+1) – f(x-1) 二阶导数的计算公式为:df(x)= f(x+1) + f(x-1) – 2f(x);
稍微难一点的则是基于高斯的一阶导数与二阶导数求取,首先看一下高斯的1D与2D的
公式。一维高斯对应的X阶导数公式:
二维高斯对应的导数公式:
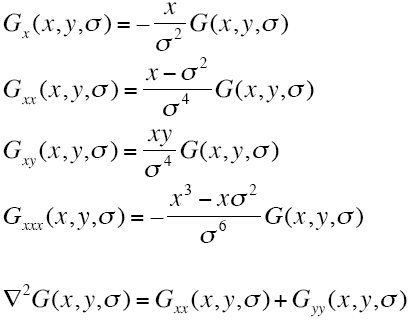
二:算法实现
1. 高斯采样,基于间隔1计算,计算mask窗口计算,这样就跟普通的卷积计算差不多
2. 设置sigma的值,本例默认为10,首先计算高斯窗口函数,默认为3 * 3
3. 根据2的结果,计算高斯导数窗口值
4. 卷积计算像素中心点值。
注意点:计算高斯函数一定要以零为中心点, 如果窗口函数大小为3,则表达为-1, 0, 1
三:程序实现关键点
1. 归一化处理,由于高斯计算出来的窗口值非常的小,必须实现归一化处理。
2. 亮度提升,对X,Y的梯度计算结果进行了亮度提升,目的是让大家看得更清楚。
3. 支持一阶与二阶单一方向X,Y偏导数计算
四:运行效果:








 本文介绍了图像处理中高斯一阶和二阶导数的重要性,用于特征和边缘提取。讨论了一阶导数反映灰度梯度变化,二阶导数用于提取图像细节和梯度变化。讲解了基于高斯的导数计算公式,并概述了算法实现步骤,包括高斯采样、计算导数窗口、卷积计算和归一化处理。最后展示了算法运行效果。
本文介绍了图像处理中高斯一阶和二阶导数的重要性,用于特征和边缘提取。讨论了一阶导数反映灰度梯度变化,二阶导数用于提取图像细节和梯度变化。讲解了基于高斯的导数计算公式,并概述了算法实现步骤,包括高斯采样、计算导数窗口、卷积计算和归一化处理。最后展示了算法运行效果。
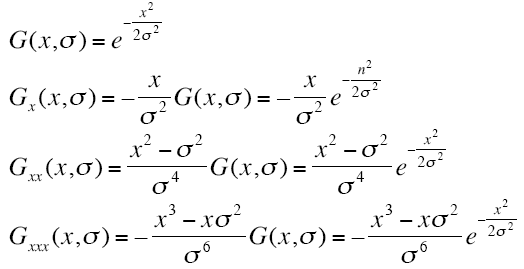
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 225
225

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








