1.非线性处理与线性处理的差别
上一篇博文的内容,是关于均值滤波器的。比方说像算术均值滤波器,几何均值滤波器。这以类型的滤波器的经常被用于剔除某些不须要的频率成分,或者选择须要的频率成分,从而达到去噪的目的。这种滤波器,被称为线性滤波器。
然而,另一些特殊滤波器,他们被称为非线性滤波器。其代表为中央值滤波器。所谓中央值滤波器,就是将一定范围内的数据(对于图像而言,是像素的灰度值)进行排序,选择中央值作为滤波器的输出。
中央值滤波器的目的并非频率成分的选择,而是求root信号。关于root信号的定义,[文献1]中是这样给出的。
------------------------
定义:对于随意信号,使用中央值滤波器进行有限次处理,直到所得到的限号不变为止。中央值滤波器处理前后,假设这个信号列没有不论什么变化,那么将这个信号列称为这个滤波器的root信号。
------------------------
对于中央值滤波器来讲,能够完美去除被椒盐噪声污染的root信号。对于root信号,有例如以下的性质。对于下面定理的证明与具体说明,请參考[文献2][文献3]。
=============
定理1:假设信号列{x(i)}是单调递增或单调递减的,那么对于不论什么尺寸的中央值滤波器,这个信号列都是root信号。
定理2:假设信号列{x(i)}是在从i開始的m个信号之间的局部单调信号的话,那么对于尺寸为N=2M+1(M<=m-2)的中央值滤波器,这种信号为这个滤波器的root信号。
=============
2.几个典型的非线性滤波器
2.1 中央值滤波器 (Median Filter)
正如第一节所叙述的,中央值滤波器能够有效去除椒盐噪声,而且不会使得图像模糊。我们将一副图像染上椒盐噪声,然后使用不同尺寸的中央值滤波器去进行处理。所得的结果的画质使用SSIM去评价。
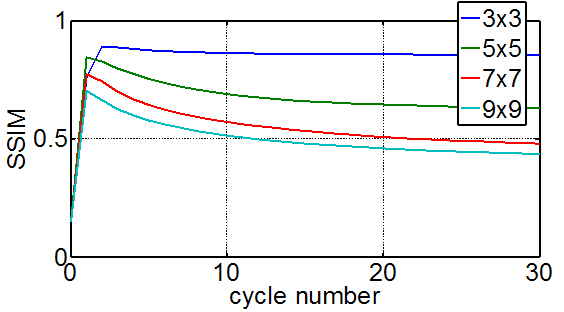
首先,将图像染上盐粒密度为0.15,胡椒密度为0.15的椒盐噪声,使用3x3,5x5,7x7和9x9四种不同尺寸的中值滤波器去处理图像。所得到的结果,例如以下表所看到的。
由上图所看到的,能够看出,所用滤波器尺寸不同,得到的结果是不同的,尺寸较大的滤波器得到了不太好的结果。随着循环次数的添加,图像的SSIM逐渐变化,最后趋近于稳定。以下是循环次数为30时候,4种尺寸滤波器得到的结果。
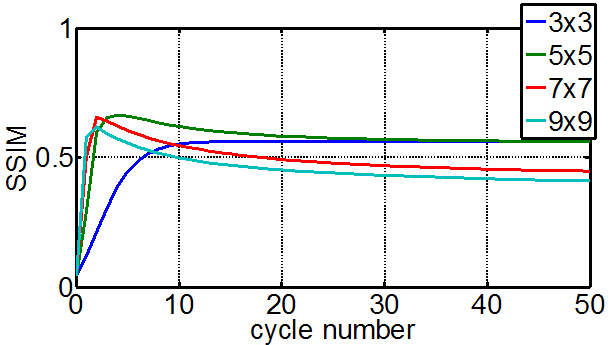
为了验证噪声与实验结果的影响,将图像染上盐粒密度为0.35,胡椒密度为0.35的椒盐噪声,在进行滤波实验,能够得到例如以下曲线。
实验结果给出,尺寸较小的的中值滤波器,其收敛到root信号较为缓慢,其次,对于高噪声的图像,其修复结果是不太好的。
总结上述实验,能够得到三个实用的结论。
1.中央值滤波器在处理过程中,不断在寻找root信号。重复数回之后,其结果收敛,基本不改变。
2.对于不同的图像,不同的噪声,最适合本幅图像的中央值滤波器的尺寸是不同的。并非尺寸越小越好。
3.尺寸小的滤波器,收敛速度慢。反之,尺寸大的滤波器,收敛较快。
2.2 自适应中央值滤波器
我们要非常好的使用中央值滤波器,仅仅有一个要点!就是找一个最适合的滤波器尺寸,使得原图就是这个滤波器的root信号,那么,就能够得到一个完美的结果(当然,最适合的滤波器是不存在的)。那么,这里就能够有个想法了,在运行滤波器操作的时候,尽可能多的尝试各种尺寸,选择一个最适合的,让原图非常接近这个尺寸的滤波器的root信号。这种话,就能够得到一个不错的结果了。当然,之对于椒盐噪声的话,还能够增加这样一个功能,因为噪声的灰度值是已知的(盐粒噪声为1,胡椒噪声0),那么仅仅有其中央值不是0或者1的时候,滤波器生效,否则,扩大滤波器尺寸。
归纳上述思想,能够得到例如以下的伪代码。
START: S_xy = read(f(x,y),[size_S_xy]);
z_min = min(S_xy);
z_max = max(S_xy);
z_med = median(S_xy);
LOOP A : A_1 = z_med - z_min;
A_2 = z_med - z_max;
if ((A_1 >0) and (A_2 < 0))
goto LOOP B;
else size_S_xy++;
goto START;
if (size_S_xy <= size_max)
g(x,y) = z_med;
goto NEXT;
LOOP B : B_1 = f(x,y) - z_min;
B_2 = f(x,y) - z_max;
if ((B_1 >0) and (B_2 < 0))
g(x,y) = f(x,y) ;
goto NEXT;
else g(x,y) = z_med;
goto NEXT;
NEXT : x,y移动到下一个像素点
if (x > x_max)and(y>y_max)
return;
else goto START;
2.3 最大值滤波器与最小值滤波器
因为这个非常easy,结果就不贴了。
2.4 中点滤波器(midpoint filter)
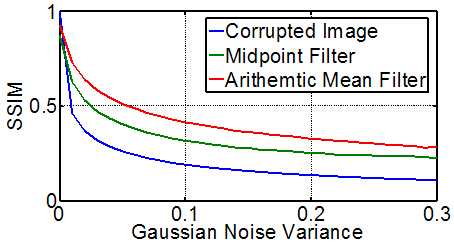
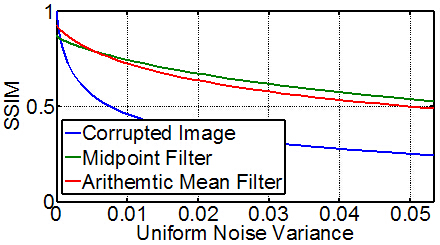
中点滤波器,糅合了均值滤波器和非线性的排序处理。这种滤波器对于去除高斯噪声与均匀噪声有非常好的效果。
我们使用这个滤波器,与平均滤波器做个比較吧。其结果显示在下图。
图片上,纵轴表示画质SSIM,横轴表示噪声的方差。绿线表示中点滤波器,红线表示算术滤波器。能够看出,均匀噪声上,中点滤波器的性能还是优于算术平均滤波器的。(当然,这可能跟选用的评价图像有关,可是基本是这个趋势)。
2.4 修正的阿尔法均值滤波器
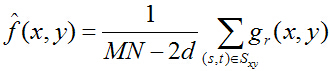
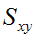 的
的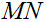 个数据进行排序,从大到下的顺序去除
个数据进行排序,从大到下的顺序去除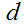 个数据,从小到大的顺序去除
个数据,从小到大的顺序去除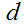 个数据。将剩下的数据计算均值。
个数据。将剩下的数据计算均值。
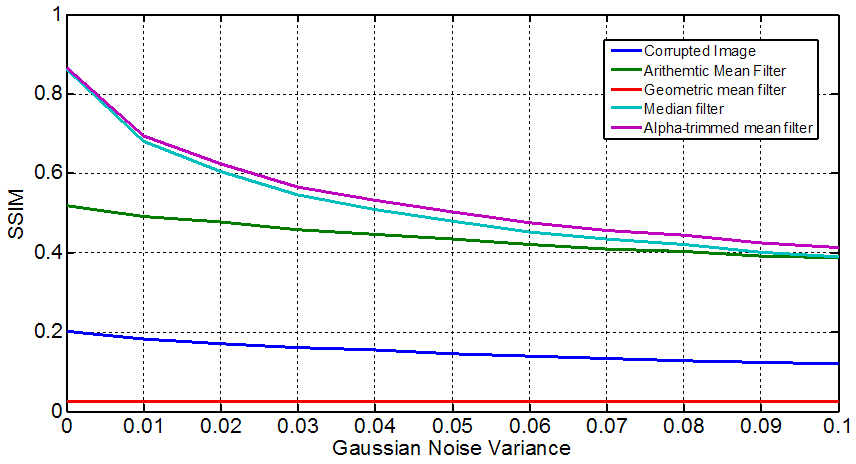
这种滤波器,非常擅长去除椒盐噪声与其它类型噪声一起污染过的图片。依旧是实验,首先将图片染上盐粒密度为0.1,胡椒密度为0.1的椒盐噪声。然后,再将这幅图像染上高斯噪声。在将图片进行去噪。得到的结果例如以下所看到的。
能够出,对于复数的噪声,这种滤波器的效果是最好的。
3.自适应中值滤波器的Matlab代码
因为本次代码都比較简单,主要是概念上的理解,所以,代码我也就贴个自适应滤波器的代码就完事吧!下一篇博文,会说到去卷积处理。
參考文献
[文献1]非線形ディジタル信号処理 ,棟安実治 ・田口亮 著,システム制御情報学会,朝倉書店,1999年03月20日
[文献2]Tyan, S. G. "Median filtering: Deterministic properties." Two-Dimensional Digital Signal Prcessing II. Springer Berlin Heidelberg, 1981. 197-217.
[文献3]Gallagher Jr N C, Wise G L. A theoretical analysis of the properties of median filters[J]. Acoustics, Speech and Signal Processing, IEEE Transactions on, 1981, 29(6): 1136-1141.
原文发于博客:http://blog.csdn.net/thnh169/
=============更新日志===================
2014 - 7 - 17 修正了一些格式错误








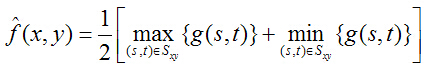

















 5920
5920

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








