正文共：872 字
预计阅读时间： 3 分钟
数学部分难度：需要了解球体、柱体、锥体体积公式
还记得课本上是怎样推导球的体积公式的吗？
球体体积公式：
一个常见的方法是祖暅(gèng)原理，下面的动图解释的就是它：
下图左边是一个半径为r的球体，右边是一个和球体一样高(H=2r)，底面半径和球体半径相同的圆柱，圆柱当中被挖去了两个圆锥(想像一个沙漏的形状)。
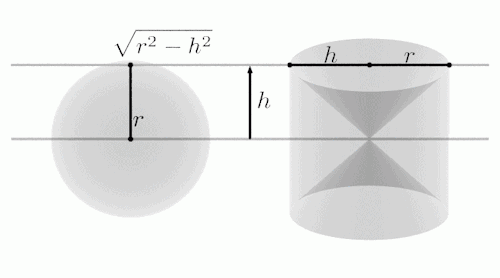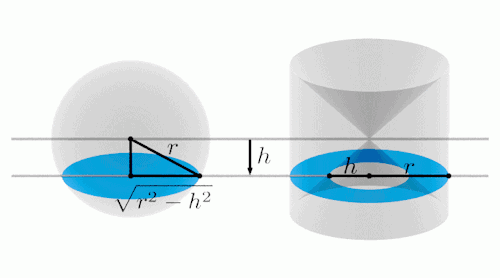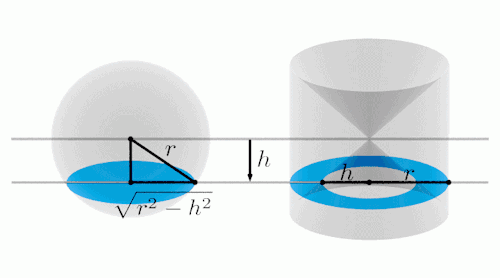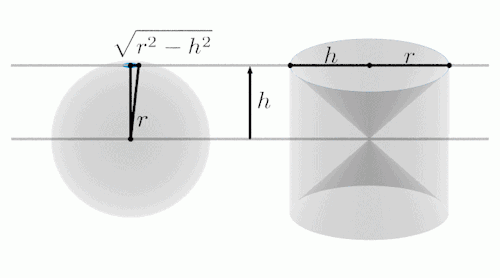
用一个平面去截这两个几何体，注意变化过程中，左右两边蓝色部分表示截面。
从俯视图方向看：
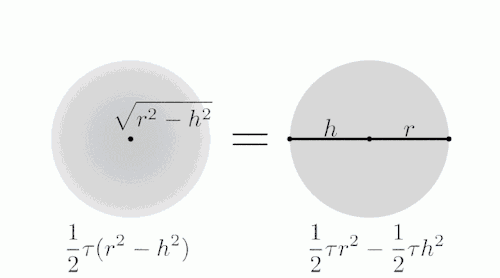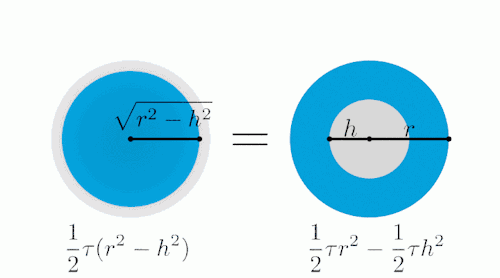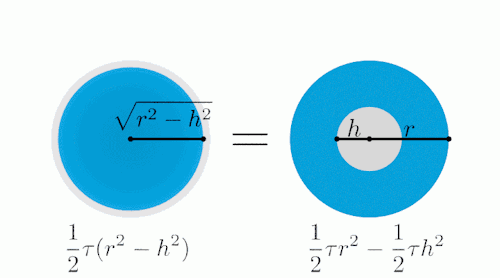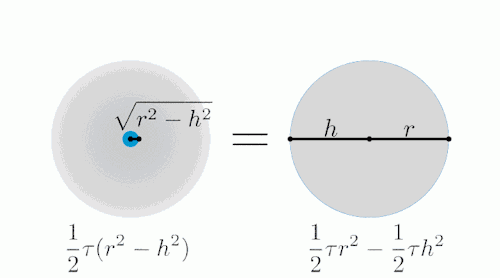
经过计算我们可以得出，变化过程中，两个截面面积相等。
几何体体积可以看做是无数个“薄片”堆积起来得到的。
由此我们能够猜测：左侧的球和右边的这个“大沙漏”，体积是完全相同的！
图片来源：Hyrodium's Graphical MathLand
祖暅原理，在西方叫卡瓦列里原理(Principio di Cavalieri)。它说的是如果两个几何体在每一个相同高度处的截面积都相同，则它们的体积也相同。
从上面的图中可以看出，如果把底面半径为r、高为2r的圆柱体挖去两个高为r的圆锥，再把剩余部分与半径为r的球体进行逐层比较，可以发现二者在每个高度上的截面积都是相等的。
这样一来，用圆柱和圆锥的体积公式就可以推出球体积公式了：
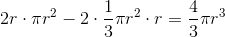
学过高数的同学可能会发现：这不就是说二重积分能够通过逐次积分来计算吗？的确，这可以看成是微积分的一个“前奏”。在17世纪上半叶，意大利数学家卡瓦列里提出了这条原理，并用它计算了一系列几何体的体积，而在17世纪下半叶，牛顿和莱布尼兹发明了微积分。
祖暅提出同样的原理是在公元5世纪，比卡瓦列里早了一千多年。
TIPS：祖暅是个名符其实的“官二代”。他出身书香门第兼官宦世家。曾祖祖昌是南朝刘宋时的大匠卿(相当于国家建工部长)；祖父祖朔之学富五车，退休后还“返聘”为皇帝的“奉朝请”；父亲祖冲之任县令、校尉等职30多年，发明创造几十件。
祖暅的父亲祖冲之
中国南北朝时期杰出的数学家之一
首次将“圆周率”精算到小数第七位
祖暅是在求球的体积公式的过程中提出这条祖暅原理的。但他还不是第一个算出球体积公式的人。
早在公元前3世纪，古希腊的阿基米德就给出了球的体积公式。他用一种奇妙的力学方法，算出半径为r的球体积是半径为r、高为2r圆柱体积的三分之二，并用穷竭法给出了证明。阿基米德的方法已经有了微积分思想的雏形，不过没有用上祖暅原理。
阿基米德的成果并没有传到中国。早期的中国数学家也研究过球的体积，但没能得到正确的结果。到了南北朝时期，祖暅终于提出了这条重要的原理：“幂势既同，则积不容异”。
·END·
和新昊老师一起感受数学之美
扫一扫
1374
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
