模型例题_初中数学：共顶点模型例题讲解（3），这个题有点难度，辅助线很关键...

昨天中午在短视频上发了这道题，本意是当作业，鼓励同学们独立思考，灵活运用，好几位同学在评论区回复，需要讲解视频，刚好录完，我们一起看下这个题的解题思路。

【例3】

如图，AB=AC=10，∠BAC=45°，BC=CD，BC⊥CD，求AD的长。

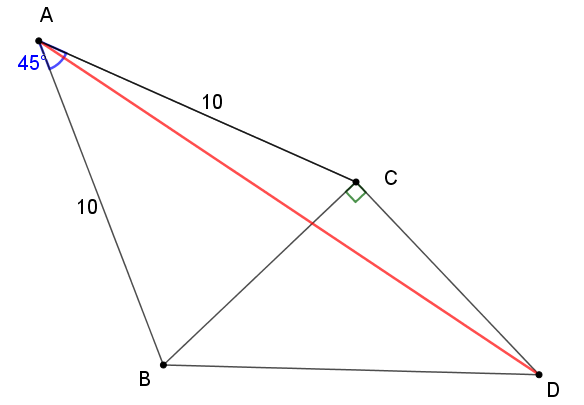
分析：题目中让求AD的长，一般情况下，初中数学求边长都会在直角三角形中利用勾股定理或者三角函数来计算，偶尔也会与相似三角形结合，边长之比等于相似比求边长。

初中数学学习圈 - 知乎​www.zhihu.com

这个题中AD没有在直角三角形中，也找不到相似三角形模型。

该怎么办才好？

转化思想，把AD转化成等长的线段求解。

题中有一个非常特殊的条件，∠BAC=45°，初中几何题遇到特殊角，往往要和直角三角形结合。

作辅助线，把线段AC绕点C旋转90°，连接AE，BE。

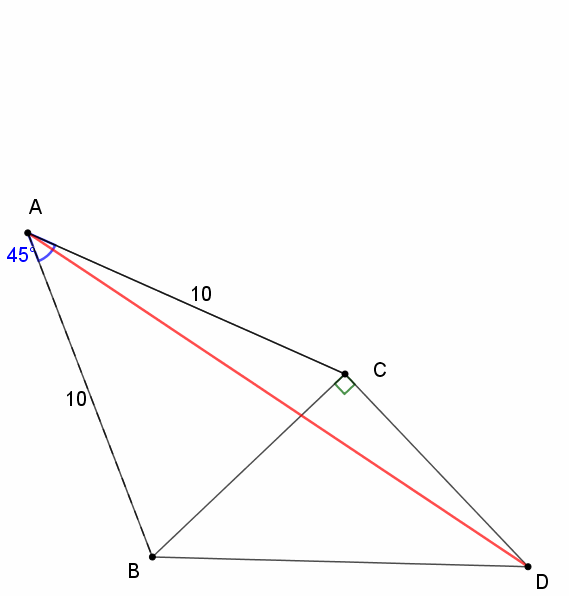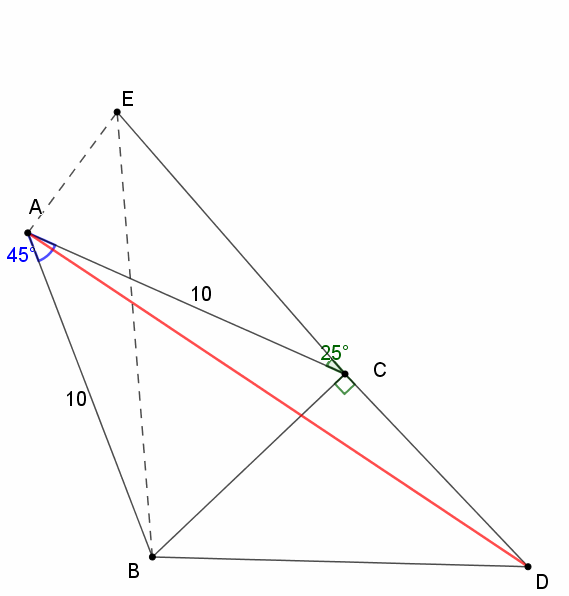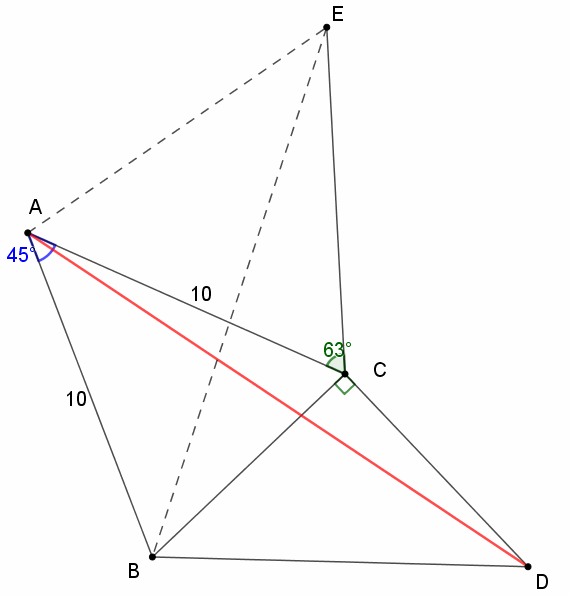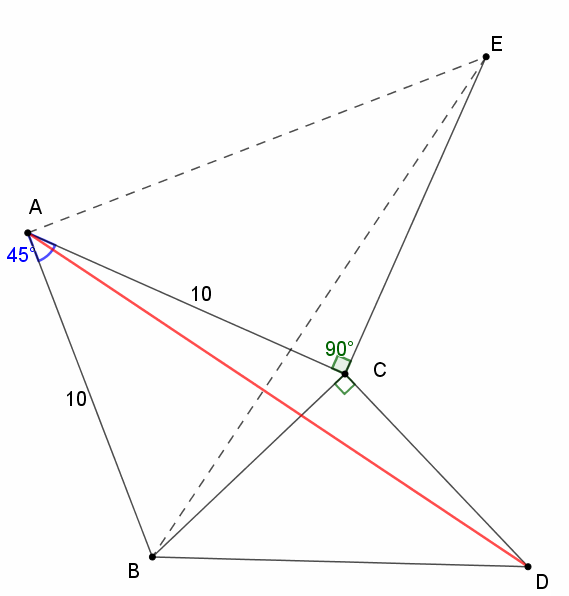
图中是不是出现了共顶点模型？

△ACE和△BCD是有公共顶点的等腰直角三角形，

所以，就会找到一组全等三角形帮助我们解题。

△BCE≌△DCA

∴AD=BE

三角形ACE是等腰直角三角形

∠CAE=45°，AE=10√2

∴∠BAE=∠BAC+∠CAE=90°

在Rt△BAE中，

根据勾股定理：

BE²=AB²+AE²

BE=10√3

∴AD=10√3

本题的视频讲解：

知乎视频​www.zhihu.com