本文介绍了三角函数中的核心概念，包括任意角、终边相同的角以及弧度制。通过数形结合的方式，阐述了任意角的概念，强调了直角坐标系在理解角旋转中的作用。此外，还提到了终边相同的角在度数和三角函数值上的关系，以及象限角和轴线角的定义。最后，文章简要讨论了弧度制的应用，包括弧度与角度的互换以及扇形的弧长和面积计算。
高中阶段，三角函数具有很重要的地位。实际学习中，一部分同学因三角公式多，产生畏难心理。
把握数形结合，抓住概念理解，理清三角公式之间内在联系，是学习三角函数化难为易的重要法门。
先看视频，
再学知识点，
重看一遍视频，
效果会不错哟。
01
任意角、终边相同的角
视频1：任意角、终边相同的角
1、为什么要建立任意角概念？
上述这些角，范围不再限于0度至360度范围之内，而且有方向。如何解决上述运动旋转角度的度量？
数学的办法就是用运动的观点来看待角的变化，从而推广角的概念形成任意角。
2、任意角概念：一条射线绕着它的端点旋转所形成的图形。为明确旋转量与旋转方向，规定如下：
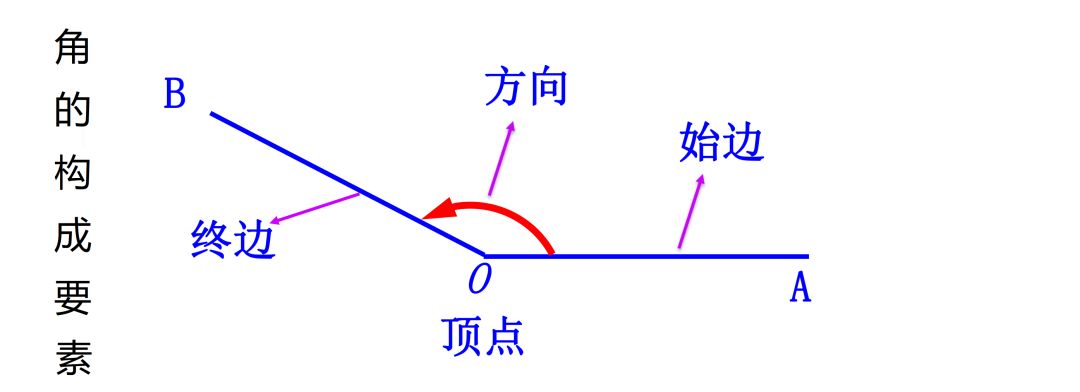
3、方法：把角放入直角坐标系中，利用直角坐标系这一工具来研究。规则是：让角的顶点与坐标原点重合，让角的始边与直角坐标系X轴的非负半轴重合。
结果：角的终边与角的度数之间建立了对应关系，使角具有了代数与几何的双重意义。
4、终边相同的角。
(1)在后续学习中，我们会知晓：
终边相同的角的三角函数完全相同。
(这样可以把角的研究范围转化到0至360度范围之内。)
(2)数量上有联系：两个终边相同的角的度数相差360度整数倍;
终边相同的角不一定相等，
相等的角终边一定相同。
02
象限角、轴线角
视频2：象限角的讲解
3、终边落在哪一象限就是哪一象限的角。
备注：在后续求解角的范围时，我们的结果表述，一般先写出0度至360度范围内角的范围，再迭加360度整数倍。
4、轴线角：终边在坐标轴上的角。
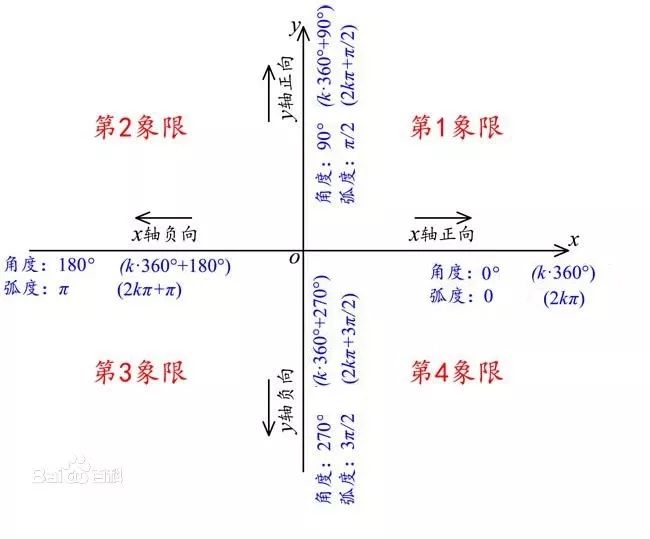
03
弧度制与扇形面积计算
视频3：弧度制与弧度制应用。
4、理解弧度概念，进而习惯弧度制下角的运算。
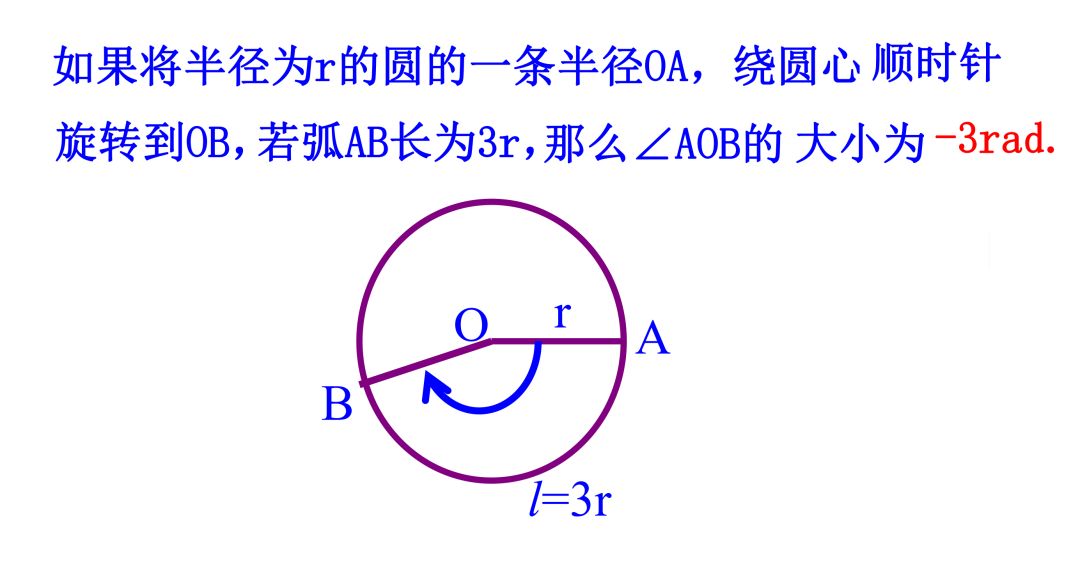
实际学习中注意两点；
(1)准确熟练进行角度与弧度的互化。
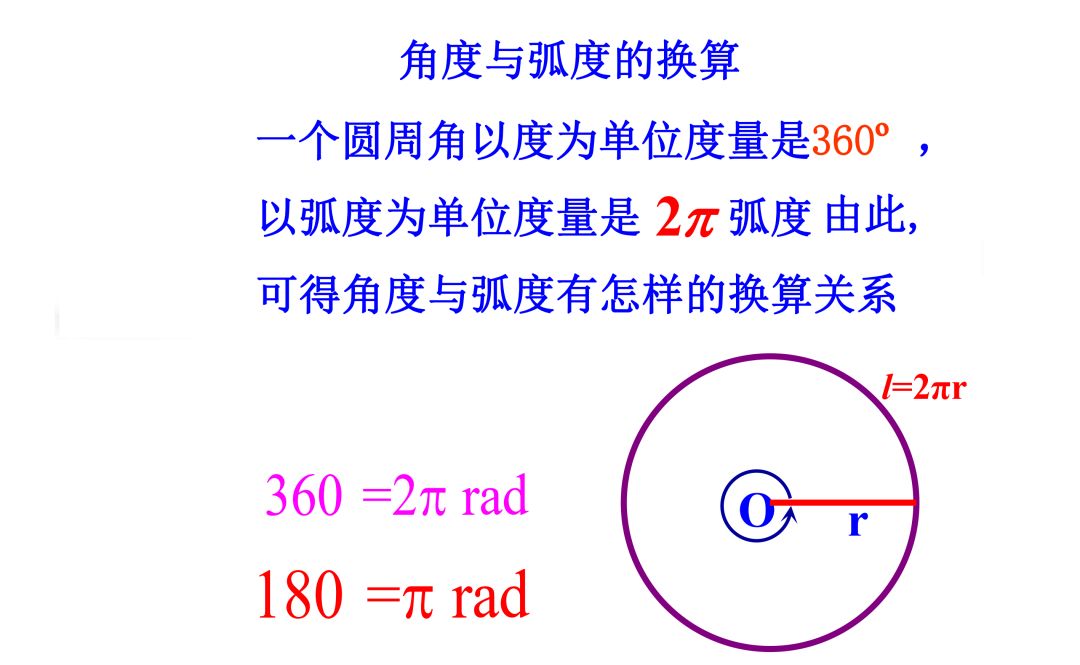
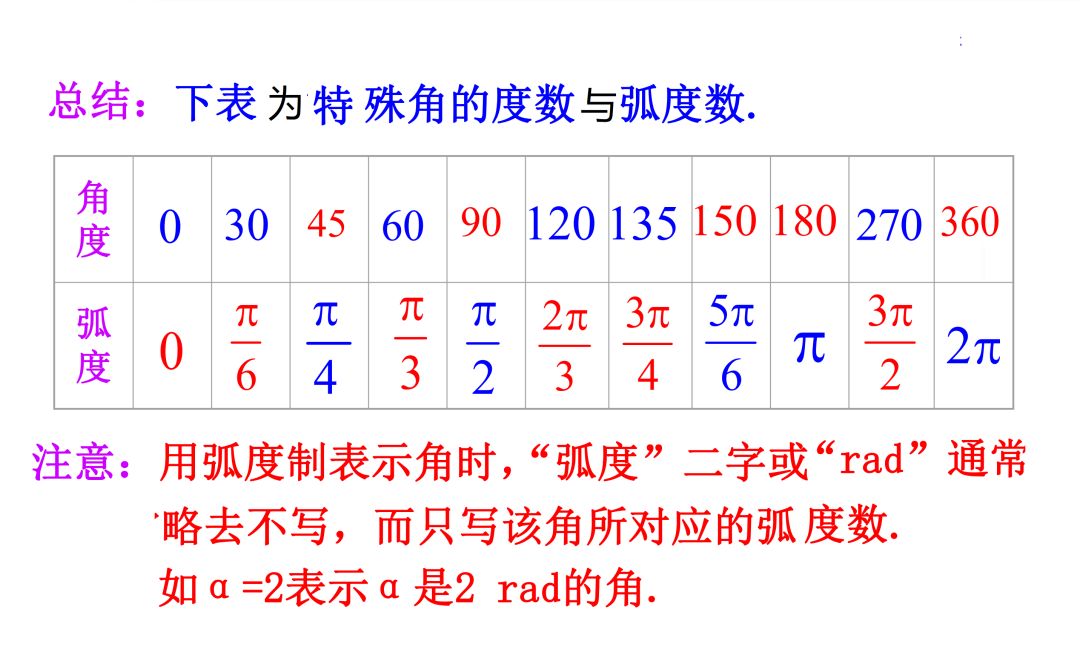
(2)弧度制下的角可以与数轴上点一一对应起来。对于弧度制表示的角放在坐标系中时，要快速准确判定终边的位置。
5、弧度制下，扇形的弧长、面积计算公式要能熟练准确运用。
备注：扇形可以看作是一个曲底的等腰三角形，圆弧相当于三角形的底、半径相当于底上的高。这样类比，公式在形式上就与三角形面积公式很好的吻合了。
人生有缘才相遇 扫码相识更有趣
人生有缘
扫码相识
视频学习
天然有趣
扫一扫
4796
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
