[编辑]
什么是图像数字化
一幅黑白静止平面图像(如照片)中各点的灰度值可用其位置坐标(x,y)的函数f(x,y)来描述。显然f(x,y)是二维连续函数。有无穷多个取值。这种用连续函数表示的图像无法用计算机进行处理,也无法在各种数字系统中传输或存储。必须将代表图像的连续(模拟)信号转变为离散(数字)信号。这样的变换过程,称为图像数字化。
[编辑]
图像数字化的内容
图像数字化的内容包括两个方面:采样和量化。
图像在空间上的离散化称为采样。即使空间上连续变化的图像离散化。也就是用空间上部分点的灰度值来表示图像。这些点称其为样点(或像素、像元、样本)。一幅图像应取多少样点呢?其约束条件是:由这些样点,采用某种方法能够正确重建原图像。采样的方法有两类:一类是直接对表示图像的二维函数值进行采样。即读取各离散点上的信号值。所得结果就是一个样点值阵列。所以也称为点阵采样。另一类是先将图像函数进行某种正交变换,用其变换系数作为采样值,故称为正交系数采样。
对样点灰度级值的离散化过程称为量化。也就是对每个样点值数码化,使其只和有限个可能电平数中的一个对应,即使图像的灰度级值离散化。量化也可以分为两种:一种是将样点灰度级值等间隔分档取整,称为均匀量化;另一种是不等间隔分档取整,称为非均匀量化。因为都要取整,故量化也常称为整量或整量化过程。
假定一幅图像取M*N个样点,对样点值进行Q级分档取整。那么对M,N和Q如何取值呢?
首先,M,N,Q一般总是取成2的整数次幂,如Q = 2b,b为正整数。通常称为对图像进行b比特量化。M,N可以取成相等,也可以不相等。若取相等,则图像矩阵为方阵,分析运算方便些。取不等的例子如陆地卫星图像就因实际需要而取成2340*3240。
其次,关于M,N,b(或Q)数值大小的确定。对b来讲,取值越大,重建图像失真越小,若要完全不失真重建原图像,b必须取无穷大,否则一定存在失真。这就是所谓量化误差。一般供人眼观察的图像,由于人眼对灰度分辨能力有限,用5-8比特量化就可以了。而卫星照片、航空照片等为了区别图像中灰度变化不大的目标,往往用8-12比特量化。对MyN的取值,主要依据是采样的约束条件。也就是在M*N大到满足采样定理的情况下,重建图像就不会产生失真,否则就会因采样点数不够而产生所谓混淆失真。为了减少表示图像的比特数,总是取MXN点数刚好满足采样定理。这种状态的采样即所谓奈奎斯特采样(如彩色电视编码技术等)。M*N常用的尺寸有512*512,256*256,64*64,32*32等。
再次,在实际应用中,如果给定了允许表示图像的总比特数M*N*b,对N*N和b的分配往往是根据图像的内容和应用要求以及系统本身的技术指标来选定。例如,若图像中有大面积灰度变化缓慢的平滑区域,如人头像特写照片等。则M*N采样点数可以少些,而量化比特数h多些。这样使重建图像灰度层次多些。若b太少,在图像灰度平滑区往往会出现“假轮廓”。反之,复杂的景物图像,如群众场面的照片等,量化比特数b可以少些而采样点数M*N要多些。这样不致丢失图像的细节。究竟M*N和b如何组合才能获
得满意的结果,很难讲出一个统一的方案。T.S.Huang研究了这个问题。他对三种不同特征的图像(一幅细节少的妇女头像特写照片,一幅中等细节摄影师工作照片,一幅包含大量细节的群众会场照片),改变其采样点数M*N和量化比特数b,分别进行图像质量的主观评价。总的结论是:不同的采样点数和量化比特数组合,可以获得相同的主观质量评价。
[编辑]
图像数字化的基础
由各种不同的图像传感器所获取的图像信号都是模拟量,为了能使其送往计算机或数字硬件进行运算处理,必须将这些模拟信号变为数字信号,这样的过程称为数字化,显然,数字化应包括空间采样、幅度量化和编码三个主要部分。
—、采样过程
根据信息论中的香农采样定理,图像信息的采样周期是由图像信号的上限频率所决定的。而且输入设备中的图像信号放大器带宽也受这个上限频率制约。因此,首先要分析一下图像信号的上限频率。
1、图像信号上限频率计算
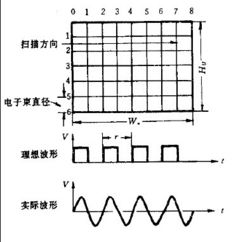
2、以电视图像为例来说明图像信号上限频率的确定方法,见图1。假设每一个小方格就是一个像素,而且.电子束正好和这些小方格重合,那么扫描这些像素所得电信号的频率就是图像信号的最高频率(即上限频率)。
设图像横向长度为Wh,纵向长度为Hu,横纵比为4/3。
设纵方向上有N'个像素,且纵横方向分解力相等,则横方向的像素数M应为:
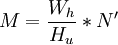 ,实际一帧图像纵方向扫描行数N总是大于N'。这是因为有场消隐行数的存在。故要乘一个系数ku,另外由于扫描线与像素间相对位置影响,还要乘一个系数k(也称垂直分解力系数)。因此,N’和N关系如下:
,实际一帧图像纵方向扫描行数N总是大于N'。这是因为有场消隐行数的存在。故要乘一个系数ku,另外由于扫描线与像素间相对位置影响,还要乘一个系数k(也称垂直分解力系数)。因此,N’和N关系如下:
N' = k * ku * N
式中
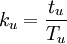 ,tu为场扫描正程时间,Tu为场扫描周期。由此可以求出水平方向所能传送的像素数M。
,tu为场扫描正程时间,Tu为场扫描周期。由此可以求出水平方向所能传送的像素数M。
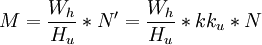
设Th为行扫描周期,th为行扫正程时间,那么横方向每一个像素所需时间T为:
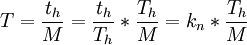
从图1可以看出图像信号的最小周期应是扫描过二个方格(像素)所需要的时间,那么其倒数即为图像的最高频率fmax:
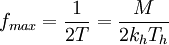
设帧周期为Tp,帧频为fp,那么
Th = Tp / N = 1 / Nfp
则最高图像频率fmax应为fmax=
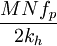 =
=
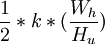
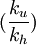
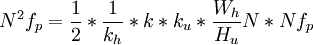
我国电视制式,N=625, fp = 25,场周期20ms,场回扫1.6ms,行周期为64us,行回扫为11.8-12us,那么
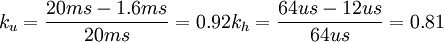
一般情况下k取0.7-0.8, Wu / Hh = 4 / 3。代入上式即可求出
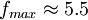 MHz其它的扫描方式输入图像信号一最高频率计算原理方法是一样的。
MHz其它的扫描方式输入图像信号一最高频率计算原理方法是一样的。
2.采样预率的计算
有一了图像信号的最高频率fmax,不丢失信息的采样频率fs应大
于或等于2fmax采样周期ts应小于或等于1 / 2fmax。对625行50场
电视制式的图像其采样周期t为:
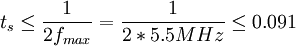 us
us
ts是理沦计算结果,实际工程应用兼顾设备价格,往往取稍大于ts,从理论上讲不满足采样定理,就会产生混淆失真,但实际应用中,这样的图像质量是允许的。例如取ts = 0.125us,稍大于0.091us,但此采样频率
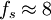 MHz,可以直接山行频分频而来,这就方便多了。再如图像处理系统中,为了运算方便,往往把图像分辨率取为512*512,则采样周期
MHz,可以直接山行频分频而来,这就方便多了。再如图像处理系统中,为了运算方便,往往把图像分辨率取为512*512,则采样周期
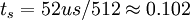 us,即采样频率
us,即采样频率
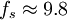 MHz。
MHz。
一般情况下是完全能够满足要求的。
3.采样点数的计算
下面我们再分析一下采样点数,仍以电视图像为例。为了减少视频信号带宽,一般电视采用隔行扫描,即分奇数场和偶数场,对625行电视系统来讲每场有312.5行。场消隐每场25行,因此实际有效行数为
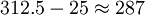 行。若采用方格采样,每场行方向最多只能取
行。若采用方格采样,每场行方向最多只能取
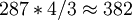 点,也就是讲若只对一场(奇数场或偶数场)采样,最大采样点数为287*382点。可见一般图像处理中使用512*512采样点阵,就必须对一帧中的两场采样。
点,也就是讲若只对一场(奇数场或偶数场)采样,最大采样点数为287*382点。可见一般图像处理中使用512*512采样点阵,就必须对一帧中的两场采样。
4.采样方式的选择
图像信号采样方式在一般情况下多采用点阵采样,就是直接对表示图像的二维函数值进行采样,读取图像函数空间各离散点的值,所得结果就是一个样点值阵列,故称为点阵采样。点阵采样可以是正方格(行和列等间隔取样点且呈正方格排列)顺序采样;也可以是针对电视图像的隔行采样;还可以是纵向采样,即每行采一点,一场采一列。点阵采样另一种是正交采样(也称平行四边形采样或六角形采样)即相邻行的采样点呈正交分布。采样方式的选择是由图像信息的应用要求决定的,分别扼要地介绍如下。
(1)正方格顺序采样:
正方格顺序采样方式就是对二维图像函数或者是扫描后的图像信号(一维时间函数)进行等间隔采样,例如对于5.5MHz带宽的电视信号,其采样频率应等于或大于11MHz。这就要求A/D变换器速率很高。一般这样高速采样数据往往先直接存入IC构成的帧存储器。再由计钟一机或数字硬件按可能的速度进行运算处理。
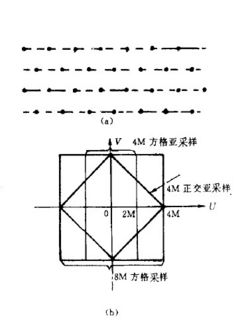
(2)正交采样
所谓正交采样,就是相邻行的采样点交义分布如图2(a)。这种采样方式在某些场合下应用是有效的。例如变化不大的人头像为主的会议电视图像,统计计算分析表明,这类图像频谱能量绝大部分集中在以原点为中心的菱形区域,而正交采样的最大不混叠区域也是呈菱形分布。图2(b)为方格采样和正交采样的最大不混叠范围。可见4MHz正交采样和8MHz的方格采样水平和垂直分辨率差不多,只是VU45。方向上稍差些。当然这种采样方式还要进行对角滤波等处理。
(3)纵向采样
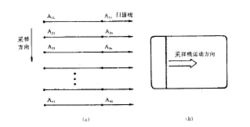
某些场合图像获取速度很快(如电视摄像机)但后面运算处理器(如微型计算机)的速度跟不上。就可以采用“快扫慢采”的方式,这就是纵向采样,如图3(a)所示。对电视信号来讲就是每行取一点,每场(或隔场)取一列,那么两个采样点间隔为行周期64us这样A/D变换器速率只要求32kHz。一幅512*512像素图像采样所需时间应为
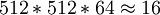 s。这种采样方式对于非实时处理是允许的,可以使器件速度要求下降,成本降低。
s。这种采样方式对于非实时处理是允许的,可以使器件速度要求下降,成本降低。
如果将纵向采样点送到监视器上,可以在显示器屏幕看到一根白左向右移动的竖线,如图3(b)所示。这根线从屏幕最左边移到最右边共需16s,也就是全图采祥时间。
二、量化过程
量化过程中要讨论的第一个问题是量化等级取多少,即通常所讲的几比特量化。从实用观点出发,因为人们的眼睛对黑白灰度级也只能区别几十个,因此供人们眼睛观察的图像有64个灰度级(即6比特)就够了。在一些要求严格的场合下,或者是计算机要对图像内容进行定量分析的系统中,往往取25fi个灰度级。在如遥感图像之类精度要求高的场合,也有取512或1024个灰度级的。若从另外角度出发,由于图像本身或成像系统存在噪声,量化级取得太多是没有必要的,因为如果噪声幅度大于量化间隔,其输出误差就会明显增加。在应用屏幕显示时,其灰度邻近区域边缘出现“忙乱”现象。假设噪声是高斯分布,均值为0,均方误差为ε2,最佳量化级的选取有两种办法:其一是令正确量化的概率大于某一值;其二是量化误差的方差等于噪声的方差。总之,量化级数的选取要按图像内
容和应用要求来决定,级数增加,精度高但数据量增加,给后面的传输处理识别增加了困难。
第二个要讨论的问题是采样幅度值如何分层,一般有两类:一类是均匀分层即所谓均匀量化;另一类是非均匀分层即所谓非均匀址化。非均匀量化的方式很多,如对供人观察的图像按人的视觉特性进行非均匀量化,即对灰度变化缓慢部分细量化,而灰度变化快的部分粗量化,还有针对人的视觉灵敏度呈对数形式的对数非均匀里化。也有从量化误差角度出发的所谓最佳量化,即使量化误差最小的非均匀量化。在最佳量化过程中,一般原则是采样值幅度概率大的细量化,反之粗量化。前几年国内外都很重视的矢量量化是结合编码技术的一种量化方式,它不是对每J个样点值进行量化,而是对样点序列进行联合量化,以便提高图像压缩比。
三、编码
编码就是对各个量化后的采样幅值数据用最少的码字去编成数码输出,作为数字化的输出一般是PCM码。但作为图像传输、存储或处理过程中的编码,内容是很多的,如信源编码日的是尽可能地压缩图像数据,以便减少图像传输速率和存储器容量以及提高运算处理速度。而信道编码往往是为了防止信道噪声引起的误码尽可能少增加一些比特数。
本条目对我有帮助5
赏
MBA智库APP
扫一扫,下载MBA智库APP
分享到:




 图像数字化涉及采样和量化两个关键步骤。采样是将空间上连续的图像离散化,量化则是对灰度级进行离散化处理。通常选择2的整数次幂作为采样点数和量化级别,以满足重建图像的要求。在实际应用中,采样点数和量化比特数的选取取决于图像内容和应用需求,以达到最佳的图像质量和数据效率。
图像数字化涉及采样和量化两个关键步骤。采样是将空间上连续的图像离散化,量化则是对灰度级进行离散化处理。通常选择2的整数次幂作为采样点数和量化级别,以满足重建图像的要求。在实际应用中,采样点数和量化比特数的选取取决于图像内容和应用需求,以达到最佳的图像质量和数据效率。
















 17万+
17万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








