傅里叶、拉普拉斯、z变换是信号与系统这门学科的灵魂。这三种变换既有联系，又有区别。无论你的专业是通信工程、电子信息工程、电气工程及其自动化、计算机科学...都需要用到这三种变换来对具体过程具体分析。可以毫不夸张的说，这三种变换对于一个理工生来说极其重要。这个学期我也在学习信号与系统，希望分享一点自己对于这门学科的认识，同时加深自己对于信号与系统认识。有不足或者错误之处，还请指正！
废话不多说，先来看一下傅里叶变换！
从数学的角度上来说，傅里叶变换、拉普拉斯变换与Z变换都是一种积分运算，本质上具有相联性，而拉普拉斯变换与Z变换都可以通过傅里叶变换导出，由此可见傅里叶变换的重要。
一、傅里叶级数
在正式介绍傅里叶变换之前，先来介绍傅里叶级数。它分为两种形式：
1.三角形式的傅里叶级数
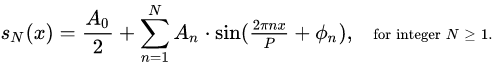
其中
从三角形式的傅里叶级数可以看出：
一个周期信号可以看成是直流分量（A0/2）、基波（
但是由于三角傅里叶级数的系数较难求解，我们一般在分析中不会采用这种形式，而转而采用第二种：
2.指数形式的傅里叶级数
综合公式：（synthesis equation）
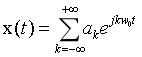
分析公式：（analysis equation）
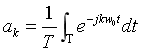
（1） 其中
（2）系数
3.傅里叶级数的收敛条件
连续时间信号的傅里叶级数收敛条件——狄利克雷条件
(1)在任何周期内，x(t)必须绝对可积，即：
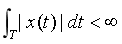
这一条件保证每一个系数
(2)在任意有限区间内，x(t)具有有限个起伏变化。也就是说，x(t)的最大值和最小值的数目有限。
(3)在x(t)的任何有限区间内，只有有限个不连续点，且这些不连续点上函数为有限值。
以上就是著名的狄利克雷条件，它是傅里叶变换存在的充分条件。
二、连续时间傅里叶变换
1.非周期信号的CTFT表示
非周期信号傅里叶变换对
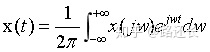
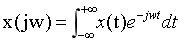
2.周期信号的CTFT表示
由于周期信号不满足狄利克雷条件中的绝对可积，如果将周期信号直接代入上面的公式，积分是不收敛的，但这并不意味这周期信号的傅里叶变换不存在。
在正式讲周期信号的CTFT之前，我们先来了解一下
由分析公式
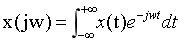
代入x(t)=
因为δ（t）的傅里叶变换是1
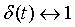
（根据单位冲激函数的筛选性质，将x(t)=δ(t)代入分析公式，很容易得出δ（t）的傅里叶变换就是1）
那么有：
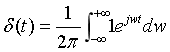
把2π乘到等式左边：
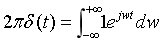
另t=-w，w=a：
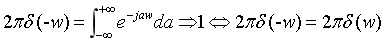
于是有：
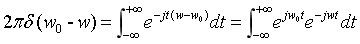
对比傅里叶变换的分析式可得：
FT（
有了上面这个变换对，我们就可以求出周期信号的傅里叶变换。
对于周期信号
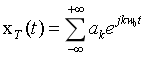
对等式两边进行傅里叶变换：
FT（
结论：周期信号的傅里叶变换是一串冲激，这些冲激位于信号频率为
三、傅里叶变换的性质
这里我们直接给出傅里叶变换性质的表格汇总
具体的证明这里就不给出了，我有性质证明的手稿，有需要的小伙伴可以私信我。上面的这些性质都需要牢记，不需要死记硬背，自己推导一遍，理解性质的含义，在这个基础之上再去背，记的会更牢。
四、常见傅里叶变换
上面这些常见傅里叶变换可以记一些比较常见的，比如单位阶跃函数、矩形波、周期方波这些比较难推导的。还是一样，如果需要这些傅里叶变换推导过程的小伙伴可以私信我。
下面对几个公式进行总结
傅里叶变换对：
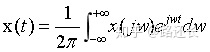
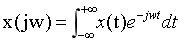
傅里叶级数：
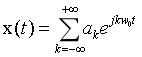
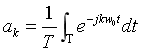
可能有小伙伴觉得这四个公式很容易混淆，我是这么记忆的：CTFS的综合式前面没有系数，那么CTFT的综合式前面就有系数；CTFS的分析式前面有系数，那么CTFT的综合式前面就没有系数。如果是离散变量（k、n）就是累加求和，如果是连续变量（t、w）就是积分。记忆方法因人而异，可以多比较总结一下，这里就不赘述了。
最后，码字不易，路过的小伙伴们点个赞再走呗(*^▽^*)后面也会陆续分享拉普拉斯变换、Z变换的笔记~
7328
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
