傅里叶变换与小波变换

傅里叶变换和小波变换是信号处理中的两种重要工具，它们都用于分析信号的频率成分，但它们有不同的特点和适用场景。

1.傅里叶变换 (Fourier Transform)

1.1基本概念

1.2特点

• 全局变换：傅里叶变换是全局性的，每个频率成分都依赖于整个信号的所有时间点。
• 频域表示：傅里叶变换将信号从时间域转换到频率域，揭示了信号中不同频率成分的幅值和相位。
• 时间信息丢失：在转换到频率域后，时间信息会丢失，即无法知道特定频率成分在信号中的具体位置。

1.3适用场景

傅里叶变换适用于分析周期信号或平稳信号中的频率成分。例如，在音频信号处理中，傅里叶变换可以揭示出不同的音调成分。

2.小波变换 (Wavelet Transform)

2.1基本概念

2.2特点

• 局部变换：小波变换是局部性的，能够提供时间和频率的局部化表示。
• 多分辨率分析：小波变换可以同时提供信号的时间和频率信息，通过调整尺度参数 ( a ) 实现不同分辨率的分析。
• 时频局部化：小波变换能够在时间和频率上进行局部化分析，适用于非平稳信号。

2.3适用场景

小波变换适用于分析非平稳信号或具有突变、瞬态特征的信号。例如，在图像处理、地震信号分析和医学信号处理（如心电图）中，小波变换能够有效揭示出信号的局部特征。

3.联系与不同之处

3.1联系

• 频率分析：两者都用于分析信号的频率成分。
• 数学基础：傅里叶变换和小波变换都基于正交基函数，傅里叶变换基于正弦和余弦函数，而小波变换基于小波函数。
• 信号重构：两者都可以实现信号的重构，傅里叶变换通过逆傅里叶变换，小波变换通过逆小波变换。

3.2不同之处

• 全局 vs 局部：傅里叶变换是全局变换，而小波变换是局部变换，能同时提供时间和频率信息。
• 时间分辨率：傅里叶变换在频域有高分辨率，但在时间域无分辨率；小波变换则具有多分辨率特性，可以在不同尺度上进行分析。
• 适用性：傅里叶变换适合平稳信号的频率分析，小波变换更适合非平稳信号的时频分析。

4.举例

下面测试不同样本并使用傅里叶变换和小波变换进行分析，然后可视化展示它们的区别和联系。

生成测试样本

生成两个测试信号，一个是由多个正弦波组成的平稳信号，另一个是包含突变和瞬态特征的非平稳信号。
在提供的代码中，生成的测试信号有以下频率成分：

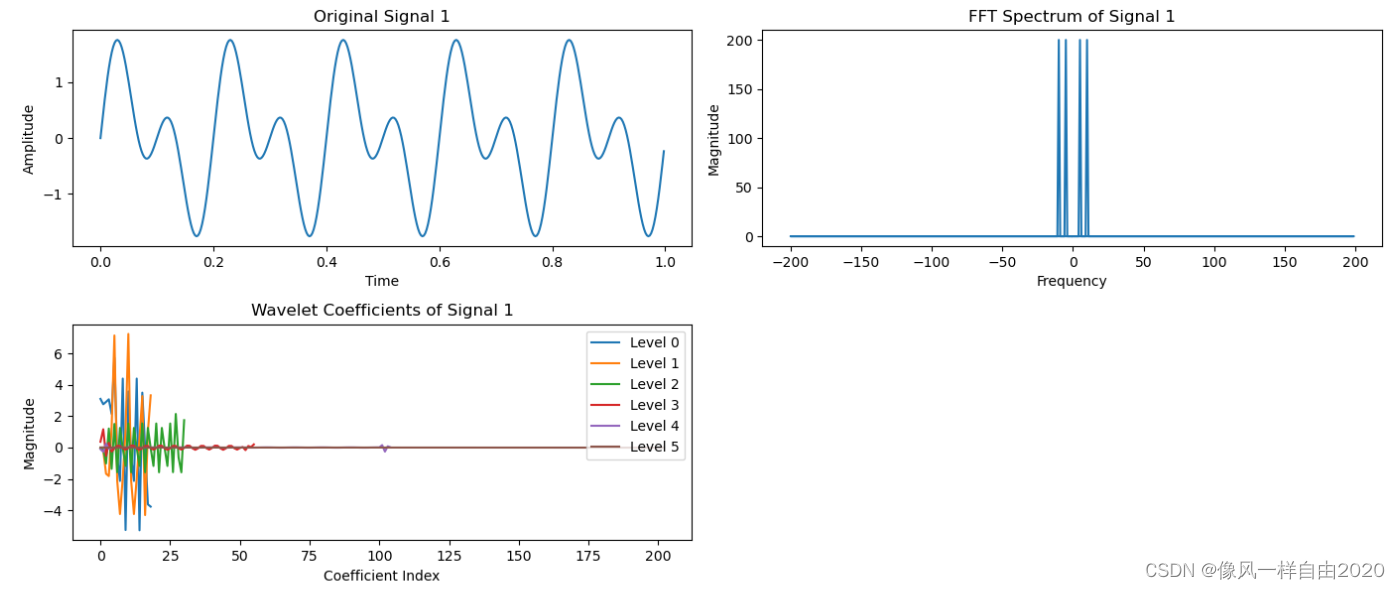
Signal 1 (平稳信号)

由两个正弦波组成：

• 一个频率为 5 Hz 的正弦波
• 一个频率为 10 Hz 的正弦波

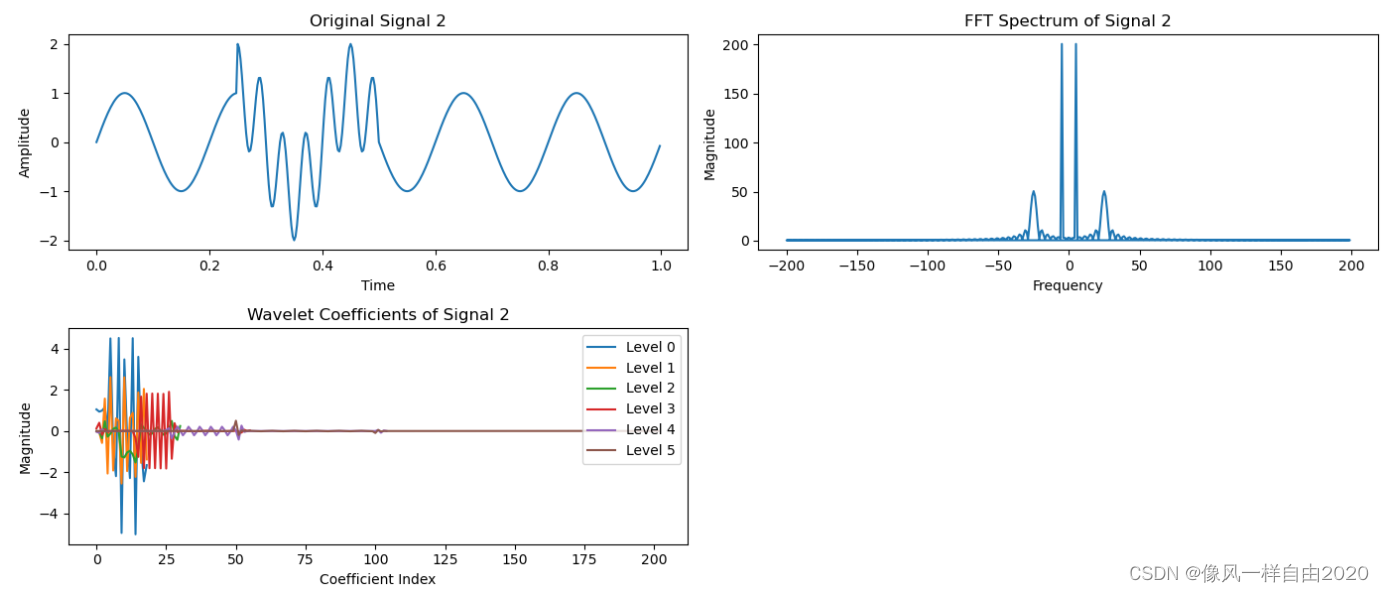
Signal 2 (非平稳信号)

由一个基本的正弦波和一个突变部分组成：

• 整个信号包含一个频率为 5 Hz 的正弦波
• 在信号的100到200样本点之间（对应时间间隔内），叠加了一个频率为 25 Hz 的正弦波

具体生成代码分析

# 时间轴生成，采样率为 400 Hz
t = np.linspace(0, 1, 400, endpoint=False)

# Signal 1
signal1 = np.sin(2 * np.pi * 5 * t) + np.sin(2 * np.pi * 10 * t)

# Signal 2
signal2 = np.sin(2 * np.pi * 5 * t)
signal2[100:200] = signal2[100:200] + np.sin(2 * np.pi * 25 * t[100:200])

在这段代码中：

• t 是时间数组，从 0 到 1 秒，共有 400 个采样点，因此采样率为 400 Hz。
• signal1 是由频率为 5 Hz 和 10 Hz 的两个正弦波组成的平稳信号。
• signal2 是一个基本频率为 5 Hz 的正弦波信号，在100到200个样本点的区间内叠加了一个频率为 25 Hz 的正弦波，形成了非平稳特征。

一言以蔽之

• Signal 1 包含 5 Hz 和 10 Hz 的正弦波成分。
• Signal 2 包含 5 Hz 的基本正弦波，并在中间区段叠加了 25 Hz 的正弦波。

代码实现

import numpy as np
import matplotlib.pyplot as plt
import pywt

# 生成时间轴，采样率为 400 Hz
t = np.linspace(0, 1, 400, endpoint=False)

# 生成平稳信号 (Signal 1)，包含两个正弦波成分
signal1 = np.sin(2 * np.pi * 5 * t) + np.sin(2 * np.pi * 10 * t)

# 生成非平稳信号 (Signal 2)
signal2 = np.sin(2 * np.pi * 5 * t)
# 在信号的100到200样本点之间，叠加一个频率为 25 Hz 的正弦波
signal2[100:200] = signal2[100:200] + np.sin(2 * np.pi * 25 * t[100:200])

# 对信号进行傅里叶变换
fft_signal1 = np.fft.fft(signal1)
fft_signal2 = np.fft.fft(signal2)
# 计算频率轴
freqs = np.fft.fftfreq(len(t), d=(t[1] - t[0]))

# 对信号进行小波变换，使用Daubechies小波 (db4)，分解到5级
coeffs1 = pywt.wavedec(signal1, 'db4', level=5)
coeffs2 = pywt.wavedec(signal2, 'db4', level=5)

# 创建图形窗口，设置大小
plt.figure(figsize=(14, 12))

# 绘制原始信号1
plt.subplot(4, 2, 1)
plt.plot(t, signal1)
plt.title('Original Signal 1')
plt.xlabel('Time')
plt.ylabel('Amplitude')

# 绘制原始信号1的傅里叶变换频谱
plt.subplot(4, 2, 2)
plt.plot(freqs, np.abs(fft_signal1))
plt.title('FFT Spectrum of Signal 1')
plt.xlabel('Frequency')
plt.ylabel('Magnitude')

# 绘制原始信号1的小波系数
plt.subplot(4, 2, 3)
for i, coeff in enumerate(coeffs1):
    plt.plot(coeff, label=f'Level {i}')
plt.title('Wavelet Coefficients of Signal 1')
plt.xlabel('Coefficient Index')
plt.ylabel('Magnitude')
plt.legend()

# 绘制原始信号2
plt.subplot(4, 2, 5)
plt.plot(t, signal2)
plt.title('Original Signal 2')
plt.xlabel('Time')
plt.ylabel('Amplitude')

# 绘制原始信号2的傅里叶变换频谱
plt.subplot(4, 2, 6)
plt.plot(freqs, np.abs(fft_signal2))
plt.title('FFT Spectrum of Signal 2')
plt.xlabel('Frequency')
plt.ylabel('Magnitude')

# 绘制原始信号2的小波系数
plt.subplot(4, 2, 7)
for i, coeff in enumerate(coeffs2):
    plt.plot(coeff, label=f'Level {i}')
plt.title('Wavelet Coefficients of Signal 2')
plt.xlabel('Coefficient Index')
plt.ylabel('Magnitude')
plt.legend()

# 调整子图布局
plt.tight_layout()
plt.show()

分析结果

通过可视化分析可以看出：

平稳信号 (Signal 1)

• 傅里叶变换：频谱中显示出明显的频率成分，对应信号中的不同正弦波。
• 小波变换：在小波系数中，不同级别上显示出信号的频率成分，具有时间和频率的局部信息。

非平稳信号 (Signal 2)

• 傅里叶变换：频谱显示出频率成分，但由于信号的非平稳性，频谱无法揭示突变和瞬态特征的具体时间位置。
• 小波变换：在小波系数中，不同级别上可以看到信号的局部特征，能够揭示信号中的突变和瞬态特征的位置和强度。

结论

傅里叶变换适用于分析信号的全局频率成分，但无法提供时间局部化信息。小波变换则能够同时提供时间和频率的局部信息，非常适合分析非平稳信号中的瞬态特征。通过结合两种变换，可以更全面地分析信号的特性。
傅里叶变换和小波变换各有优缺点，选择合的工具取决于信号的特性和分析目的。傅里叶变换在频率分析中非常强大，而小波变换在分析非平稳信号和提供时频局部化信息方面具有显著优势。