二维托盘装载问题的建模与求解

一、问题简介

二维托盘装载问题是托盘装载问题的一个特殊情况,它仅考虑了长度和宽度两个维度,忽略了高度这一维度,因此也被称为二维装箱问题(2D Bin Packing Problem)。该问题的目标是将一组不同长度和宽度的矩形箱子,无重叠地装载到一个固定大小的矩形托盘上,使得托盘的利用面积最大化，如下图所示为一个托盘装载问题的示意图。

通常而言，托盘装载问题主要包含以下约束：
（1）托盘的长宽固定
（2）箱子的长宽固定
（3）箱子之间不允许重叠
（4）所有箱子必须在托盘区域内
（5）箱子可以根据需要旋转90度

托盘装载问题的优化目标通常为最大化托盘利用面积,即装载后剩余的空余面积最小，相比三维托盘装载问题,二维版本忽略了高度这一维度的约束,问题的复杂度有所降低,但仍然属于NP难问题。常用的解决方法包括:

近似算法
（1）近似比分数算法 (APFA)
（2）最坏情况比率算法 (WSCRA)

启发式算法
（1）下一适合位置算法 (NFFA)
（2）最大空隙度算法 (LGA)

元启发式算法
（1）遗传算法
（2）模拟退火算法
（3）蚁群算法等

精确算法
（1）枚举法
（2）线性规划法等

二维托盘装载问题虽然是一个理论化简的模型,但也有现实应用场景,例如多层板条箱装载问题，纸板、木板、金属板等装载最优化，仓库地面区域规划与划分，集装箱货物装载优化等，本文首先对该问题进行建模，然后采用线性规划方法对该问题进行求解，受限于问题的复杂度，该方法仅适用于小规模的求解。

二、模型搭建

2.1 符号定义

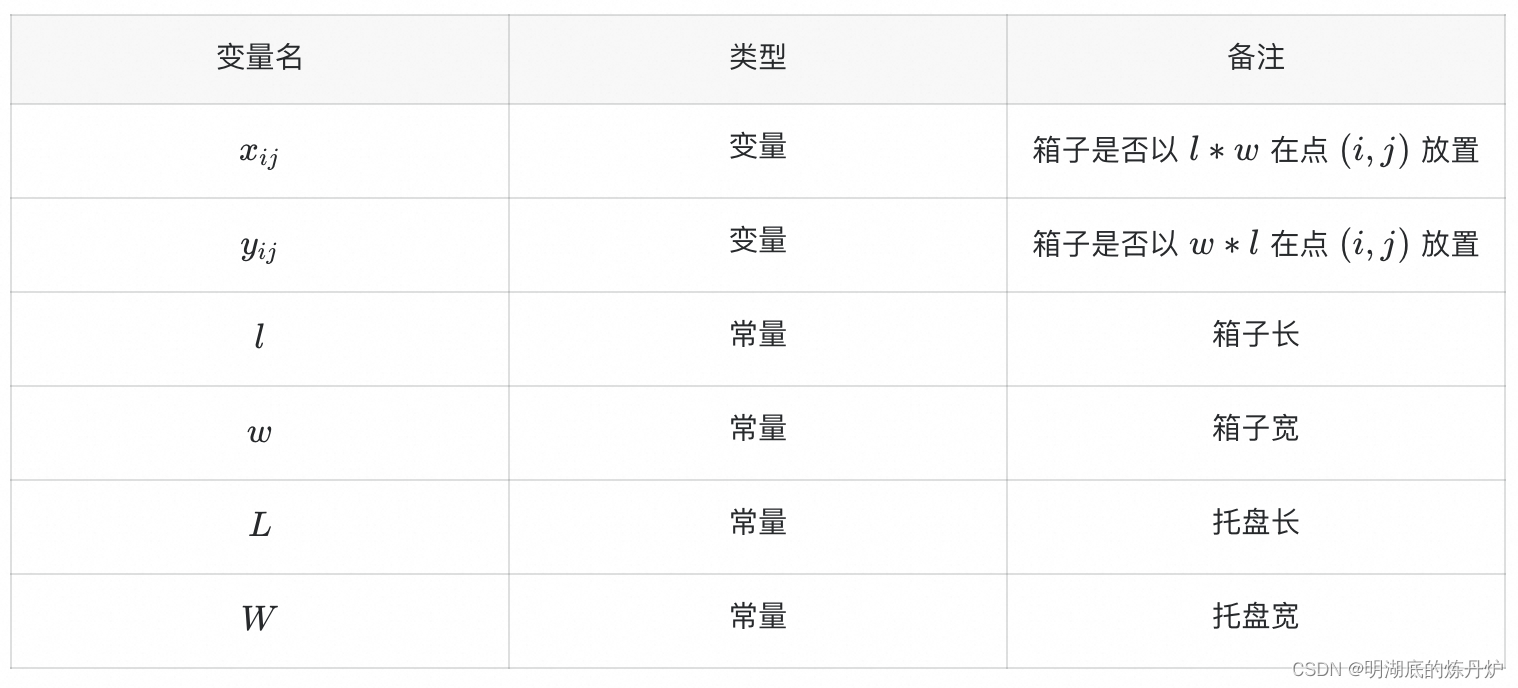
2.2 数学模型

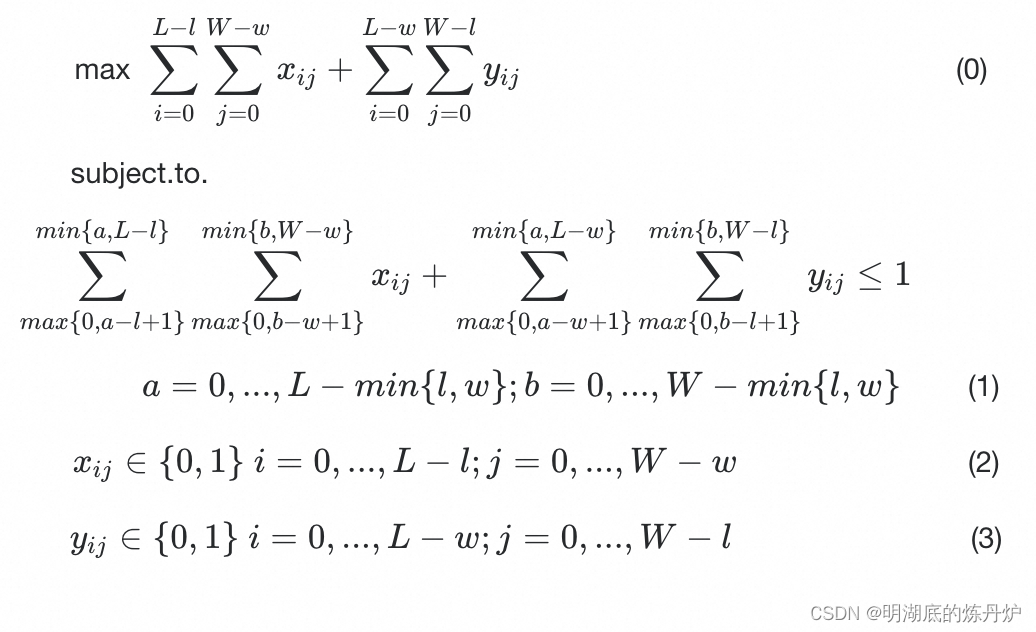
其中：
式（0）最大化装载箱子数量；
式（1）保证对于放置在托盘上的每个箱子互不重叠；
式（2）-（3）对变量类型进行约束。
稍微需要注意的是约束（1），两个箱子的边界是可以重合的，因此托盘上所有点都最多有一个箱子覆盖这样的描述是不成立的。

三、核心代码

3.1 求解代码

#求解器
model=Model('pallet loading')


x,y=dict(),dict()
for i in lp:
    for j in wp:
        x[(i,j)]=model.addVar(vtype='B',name='x[{}][{}]'.format(i,j))
        y[(i,j)]=model.addVar(vtype='B',name='y[{}][{}]'.format(i,j))

#目标函数
obj=0
for i in lp:
    for j in wp:
        if i+a<=L and j+b<=W:
            obj+=x[(i,j)]
        if i+b<=L and j+a<=W:
            obj+=y[(i,j)]
model.setObjective(obj,sense='maximize')
            

#坐标点s和r
for r in range(L):
    for s in range(W):
        expr=0
        for i in lp:
            for j in wp:
                if (i<=r and i+a>r) and (j<=s and j+b>s) and i+a<=L and j+b<=W:
                    expr+=x[(i,j)]
                if (i<=r and i+b>r) and (j<=s and j+a>s) and i+b<=L and j+a<=W:
                    expr+=y[(i,j)]
        if expr:
            model.addCons(expr<=1,name='({},{})'.format(r,s))

#求解
model.optimize()

3.2 可视化代码

def plot_box(points,puts,L,W):
    separate=10
    colors = ['#00FFFF','#7FFFD4','#000000','#0000FF','#8A2BE2',
                '#A52A2A','#DEB887','#5F9EA0','#7FFF00','#D2691E',
                '#FF7F50','#6495ED','#DC143C','#00FFFF','#00008B',
                '#008B8B','#B8860B','#A9A9A9','#006400','#BDB76B']
    plt.figure(figsize=[20,20*W/L])
    plt.xlim(0,L)
    plt.ylim(0,W)
    num=len(points)
    for i in range(num):
        point=points[i]
        put=puts[i]
        if put=='x':
            for l in range(b*separate+1):
                plt.plot([point[0]+i for i in range(a+1)],[point[1]+l/separate for i in range(a+1)],color=colors[i%len(colors)])
            plt.plot([point[0] for i in range(b+1)],[point[1]+i for i in range(b+1)],color=colors[i%len(colors)])
            plt.plot([point[0]+a for i in range(b+1)],[point[1]+i for i in range(b+1)],color=colors[i%len(colors)])
        if put=='y':
            
            plt.plot([point[0]+i for i in range(b+1)],[point[1] for i in range(b+1)],color=colors[i%len(colors)])
            plt.plot([point[0]+i for i in range(b+1)],[point[1]+a for i in range(b+1)],color=colors[i%len(colors)])
            for w in range((b)*separate):
                plt.plot([point[0]+w/separate for i in range(a+1)],[point[1]+i for i in range(a+1)],color=colors[i%len(colors)])

四、测试结果

在这一小节中，用两个case来验证本文算法的有效性，第一个case规模较小，第二个case规模较大，求解时间较长，基本临近线性规划的求解极限。

4.1 简单case

在长宽分别为11、10的托盘中，放置长宽分别为4、3的箱子，最多放置的箱子数量为9，放置结果如下图所示。

4.2 复杂case

在长宽分别为200、100的托盘中，放置长宽分别为15，10的箱子，最多放置的箱子数量为133，放置结果如下图所示。

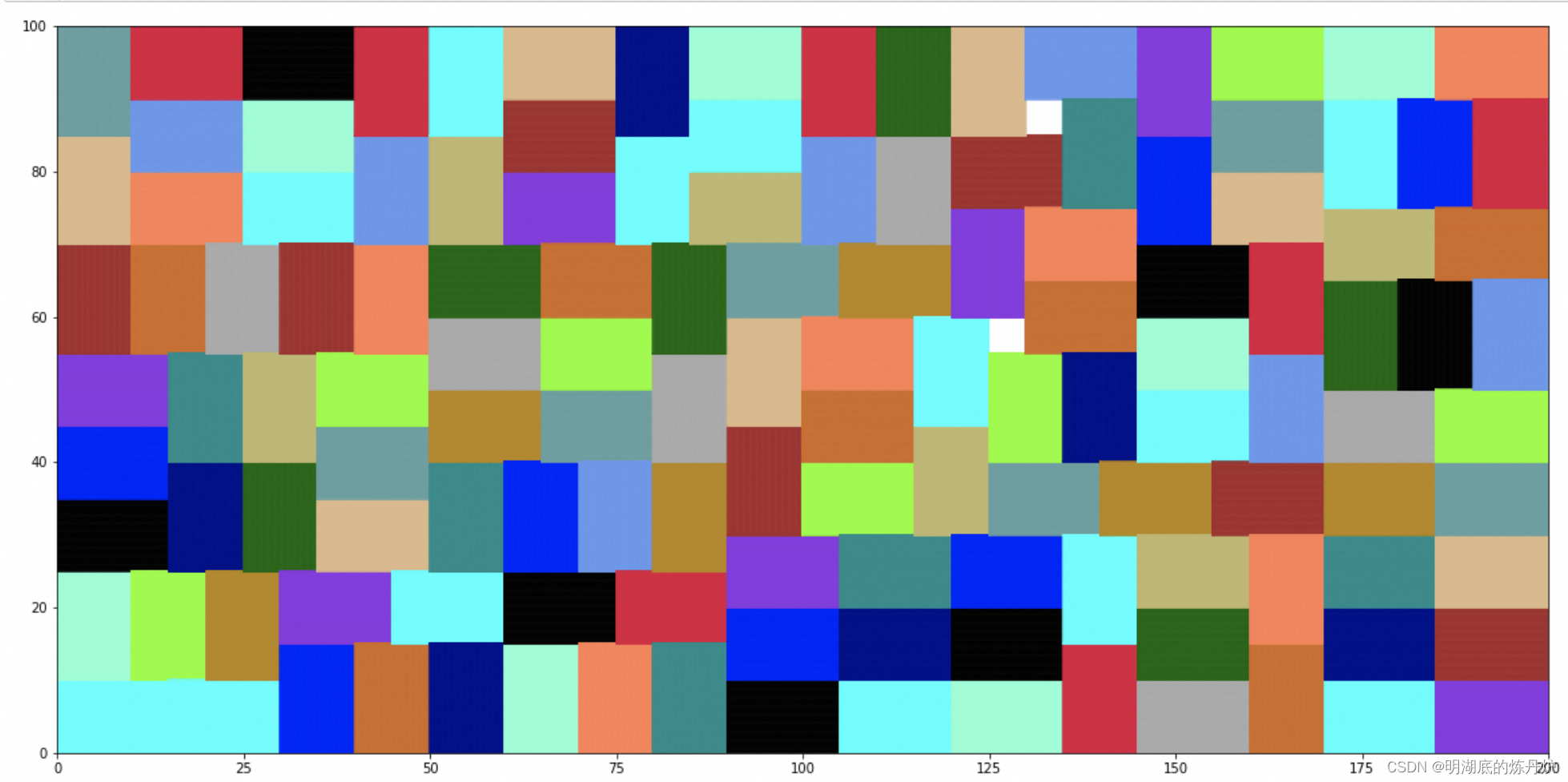
对于第二个case，直接求解其实还是比较有难度，为了加速求解，对可放置点进行了稀疏处理，理论上托盘上的最优放置点可以表示为：

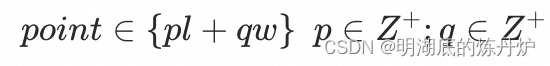
该稀疏解不损失最优性，证明过程在论文中多有提及，不再赘述。