各类曲线的参数方程_初学讲义之高中数学十七：参数方程

参数方程是圆锥曲线方程的一种

它既是很好的解题工具，可以把部分解析几何题——特别是圆和椭圆——变得非常简便

它也是考察的内容，有时候题目会把参数方程作为背景知识用在考题中

因此，掌握参数方程对解决比较难的题目是很有帮助的

一般方程与参数方程

一般的圆锥曲线方程，往往是关于两个变量x和y的方程

它的一个重要特征是：轨迹上点的坐标（x，y）直接出现在方程里，x和y的关系直接用方程来表示

比如直线的

圆的

椭圆的

双曲线的

抛物线的

参数方程就不一样了

轨迹上点的坐标（x，y）并不直接出现在方程里

x和y分别由以参数为自变量的函数来表示

x和y的关系通过只包含参数的方程来表示

参数方程最大的优点，就是只有一个自变量

x和y都用这个参数来表达

x和y的关系式原本有两个变量（x和y），用参数表达后就只有参数自己一个未知数了，

直线的参数方程

直线的方程最为简单，但是最不实用，因为直线本身已经很简单了

对于解题来说，直线的参数方程比直线的一般方程要麻烦地多，因此并不用掌握

但是为了更好地理解参数方程，还是要从直线的参数方程开始讲

首先，还是用平面直角坐标系来表示直线，它上面点的坐标为（x，y）

就假设这条直线为

现在引入一个新的参数：t

t 只是一个参数，与我们的平面直角坐标轴毫无关系

我们令：

（上面两个等式左边要用一个大括号“{”括起来表示联立，知乎的输入法无法实现）

这就是直线

的参数方程

这个参数方程有什么含义呢？

从两个方程系数分别为b和-a可以看出，每当t增加一个单位，x就增加b个单位，y就增加-a个单位

其实这与一般方程

或

是一个意思：

每当x增加1个单位，y增加-a/b个单位（等同于每当x增加b个单位，y增加-a个单位）

区别在于参数方程中是t在变，x和y随着t变化而变化

在一般方程中，是y随着x变化而变化，（或者说x随着y变化而变化也一样）

事实上，我们对

做个变形，用x来表示t，就是：

，

把它代入另一个方程中消去t就得到：

也就是直线的一般方程

下面来看个具体的例子：

直线 x-2y+4=0

它的一个参数方程为

x=2t+2

y=t+3

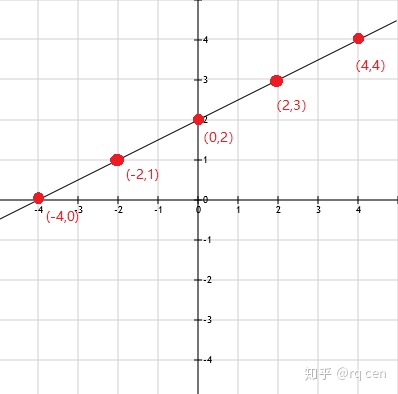
当t=1时，x=4，y=4，直线过点（4,4）

当t=0时，x=2，y=3，直线过点（2,3）

当t=-1时，x=0，y=2，直线过点（0,2）

当t=-2时，x=-2，y=1，直线过点（-2,1）

当t=-3时，x=-4，y=0，直线过点（-4, 0）

其实还有个偷懒的办法，就是直接令参数方程为：

这也是参数方程，y=f(t)与一般方程y=f(x)的表达式相同，只不过多此一举地先用t来表示x，再来表示y了

任意直线，都可以列出无数种参数方程

第一步：随便列个x关于t的一次函数：x=p*t+q

第二步：将上式代入一般方程并化简：

ax+by+c=0

a(p*t+q)+by+c=0

y=(-ap/b)t-aq/b-c/b

如同前面所示，可以偷懒地直接用x=t

总的来说，直线的参数方程在解题上毫无实用价值，因为x和y的关系已经非常简单了，引入新的参数完全是多此一举

但是，对其他复杂的曲线，用参数方程就大不一样了

圆的参数方程

先来看最简单的圆：以原点（0,0）为圆心，单位长（1）为半径的圆：

在《八：三角函数》入门中，就用的这个标准圆来讲的三角函数

用“到定点（圆心）的距离等于定长（半径）的点的轨迹”来定义圆时，我们得到了圆的标准方程，对于圆心在原点，半径为单位长的圆，就是

这个圆上每个点的坐标（x，y）都满足这个方程，这个方程的每个解都在这个圆上

除了用简单直接的（x，y）还有没有其他方式表达这个圆呢？

结合之前学过的三角函数，我们可以发现

对圆上任意点

，设半径OA与x轴正方向的夹角为α，

则

当α取从0到2π的任意值时，对应的点

都在这个标准圆上

从这个标准圆上任意一点，它的坐标都能用

来表示

因此以上这个方程组就是标准圆的参数方程

我们把

代入到圆的标准方程

左边得到：

(α∈[0, 2π])

它的值就是1

当半径为r时圆的参数方程

现在让圆稍微复杂点，圆心还在原点（0,0），半径变为 2

它的标准方程是

参数方程是什么样呢？

如果能自己推出的话，说明三角函数的基础还不错

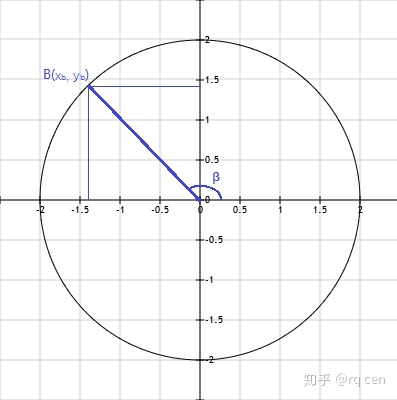
很简单，由于半径变成了2，所以圆上任意一点

的坐标满足：

也就是在参数cos、sin前面乘以2就行了

对于任意圆心在原点，半径为r的圆，它的参数方程为：

x=rcosθ

y=rsinθ （θ ∈[0,2π]）

再和标准方程比较下：

当圆心不在原点时圆的参数方程

如果圆心不在原点，而是在点（a，b），我们已经知道它的标准方程是：

那么它的参数方程是什么呢？

有两个思路：

思路一：

可以把这个圆看作是圆心在原点，半径为r的圆：

沿着向量（a，b）平移后得到的

因此这个圆上每个点的坐标就是

也就是

这就是原点在 （a，b），半径为 r 的圆的参数方程

和它的标准方程比较下：

把x和y的参数方程代入标准方程左边：

=

注意：

平面直角坐标中的平移变换是很容易出错的地方

对函数作平移变换后，比如（a，b）

相应点的坐标是加上a和b，即（x+a，x+b）

对于标准方程是应当减去a和b，即f(x-a, y-b)=0

比如圆就是，当圆心在原点的圆

，沿着（a，b）移动后，

圆心从（0,0）变为（0+a，0+b）

它上面点的坐标变为：

它的标准方程变为：

为了防止出错，可以把参数方程带入到标准方程中进行验证

以上就是圆的参数方程的全部内容，它的优点就是用a+rcosθ 和b+rsinθ 替代了x和y，把未知数变成了1个，并且可以运用三角函数的性质以及和、差、倍角、半角公式来进行运算，可以把一些题目变得简便。

---

椭圆的参数方程

椭圆与圆类似，先来比较圆心在原点的圆和椭圆的标准方程：

圆：

椭圆：

由于椭圆的几何图像拉伸起来非常复杂，也不是高中的考察内容，这里只从数学上给出参数方程：

我们只需要把圆中的cosθ变为 a*cosθ，sinθ变为b*sinθ，就得到了椭圆的参数方程：

（θ∈[0, 2π]）

把参数方程代入到标准方程左边得到：

高中数学和高考中几乎从未出现圆心不在原点的椭圆和双曲线，因此平移变换不进行专门讲解，原理很简单。

---

双曲线的参数方程

与圆和椭圆类似，双曲线也可以写出用三角函数表达的参数方程

不同的是，由于双曲线的标准方程是

它用的三角函数关系不是

而是

这个三角函数关系用的极少，如果没背下来也不要紧，稍稍转换下就可以看出：

由此可得：

双曲线

的参数方程为：

双曲线

的参数方程为：

具体谁a谁b，谁sec谁tan，代入标准方程验证一下即可

---

小结

参数方程的本质就是用一个参数分别表示x和y

高中用到的参数方程是用三角函数关系表示圆锥曲线

参数方程的最大优势就是只有一个未知数，并且可以利用三角函数关系和恒等变换来求解，求得θ后再代入x和y的参数方程就出x和y即可

参数方程的最大劣势就是变成了三角函数，三角函数的运算非常复杂，三角函数基本功不够好的同学用起来会很难

绝大多数题目用x、y的方程解起来虽然复杂，但总归是加减乘除平方开方，虽然麻烦，但麻烦的程度有限。少部分题目用参数方程（三角函数）解会很简便，大部分题目反而会更加复杂

因此参数方程最重要的一点就是判断究竟是让题目简化了还是更复杂了

判断的方法很简单也很傻，就是代进去先简单算算，要是算到某些步骤算不下去了，很可能就是不适合，也有可能是你的三角函数不够好。

相比较而言，圆和椭圆的参数方程最有用，双曲线的极少用到，直线和抛物的参数方程只会比标准方程更复杂

（因此本篇没讲抛物线的，其实和直线差不多，直线是2个一元一次函数

抛物线是一个一次的和一个二次的，二次的就和原标准方程几乎没区别）

高中平面解析几何的基本概念基本上就这些了，如果后面发现有遗漏我再补上。