两个向量平行满足什么_向量的向量积

最新推荐文章于 2021-06-29 20:39:08 发布
最新推荐文章于 2021-06-29 20:39:08 发布
阅读量3.9k 收藏 1
点赞数 1
文章标签： 两个向量平行满足什么
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_39619174/article/details/112065740
版权
本文深入探讨了向量的相关知识，包括向量的定义、数量积、向量积、三向量混合积以及双重向量积。详细解释了这些概念的定义、性质和运算规则，特别是向量积与数量积在几何和代数上的含义，以及它们在判断向量平行、垂直和平面内的关系等方面的应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

向量,是我们初高中学习的知识。我们也学习过向量积。我们今天来深入了解一下向量的各种积

1.什么是向量

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向。

2.向量积有哪些

  • 数量积
  • 向量积
  • 三向量混合积
  • 双重向量积

1.数量积

数量积定义：已知两个非零向量a,b，作OA=a,OB=b，则∠AOB称作向量a和向量b的夹角，记作θ并规定0≤θ≤π

定义：两个向量的数量积（内积、点积）是一个数量（没有方向），记作a·b。

若a、b不共线，则

74fb943055e792d8086c924115b0312c.png


若a、b共线，则

b7a8b83ce63a5d095b7690073c405785.png

向量的数量积的坐标表示：a·b=x·x'+y·y'。

向量的数量积的运算律

交换律：a·b=b·a

关于乘法的结合律：(λa)·b=λ(a·b)

分配律：a+b)·c=a·c+b·c

向量的数量积的性质

a·a=|a|^2。

a⊥b〈=〉a·b=0。

|a·b|≤|a|·|b|。（该公式证明如下：|a·b|=|a|·|b|·|cosα| 因为0≤|cosα|≤1，所以|a·b|≤|a|·|b|）

向量的数量积与实数运算的主要不同点

1．向量的数量积不满足结合律，即：(a·b)·c≠a·(b·c)；例如：(a·b)²≠a²·b²。

2．向量的数量积不满足消去律，即：由a·b=a·c(a≠0)，推不出b=c。

3．|a·b|与|a|·|b|不等价

4．由 |a|=|b| ，不能推出a=b，也不能推出a=-b，但反过来则成立。

2.向量积

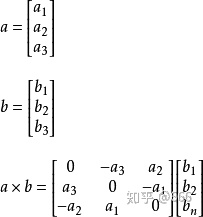
7fef499c9329148d2ed15922d221c5dc.png

定义：两个向量a和b的向量积

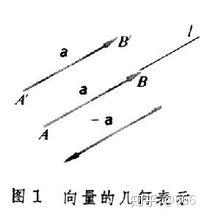
2518e4a1cb2f44e3e3ef1d64f82c395d.png

https://baike.baidu.com/pic/%E5%90%91%E9%87%8F/1396519/0/58c3acb7d9fe5eba31add18f?fr=lemma&ct=single 向量的几何表示
（外积、叉积）是一个向量，记作a×b（这里“×”并不是乘号，只是一种表示方法，与“·”不同，也可记做“∧”）。若a、b不共线，则a×b的模是：∣a×b∣=|a|·|b|·sin〈a，b〉；a×b的方向是：垂直于a和b，且a、b和a×b按这个次序构成右手系。若a、b垂直，则∣a×b∣=|a|*|b|（此处与数量积不同，请注意），若a×b=0，则a、b平行。向量积即两个不共线非零向量所在平面的一组法向量。

运算法则：运用三阶行列式

设a,b,c分别为沿x,y,z轴的单位向量

A=(x1,y1,z1)，B=（x2,y2,z2），则

d89d57682aad3112d04df6922a6e27ef.png

向量的向量积性质：

|a×b|是以a和b为边的平行四边形面积。

a×a=0。

a平行b〈=〉a×b=0

向量的向量积运算律

a×b=-b×a

(λa)×b=λ(a×b)=a×(λb)

a×(b+c)=a×b+a×c.

(a+b)×c=a×c+b×c.

上两个分配律分别称为左分配律和右分配律。在演算中应注意不能交换“×”号两侧向量的次序。

注：向量没有除法，“向量AB/向量CD”是没有意义的。

3.三向量混合积

定义：给定空间三向量a、b、c，向量a、b的向量积a×b，再和向量c作数量积(a×b)·c， https://baike.baidu.com/pic/%E5%90%91%E9%87%8F/1396519/0/5202e5f24f90c15db17ec575?fr=lemma&ct=single

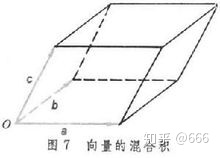
355f7b11cdad1078642c0de08423abe2.png

https://baike.baidu.com/pic/%E5%90%91%E9%87%8F/1396519/0/5202e5f24f90c15db17ec575?fr=lemma&ct=single 向量的混合积
所得的数叫做三向量a、b、c的混合积，记作(a,b,c)或(abc)，即(abc)=(a,b,c)=(a×b)·c

混合积具有下列性质：

1．三个不共面向量a、b、c的混合积的绝对值等于以a、b、c为棱的平行六面体的体积V，并且当a、b、c构成右手系时混合积是正数；当a、b、c构成左手系时，混合积是负数，即(abc)=εV（当a、b、c构成右手系时ε=1；当a、b、c构成左手系时ε=-1）

2．上性质的推论：三向量a、b、c共面的充要条件是(abc)=0

3．(abc)=(bca)=(cab)=-(bac)=-(cba)=-(acb)

4.双重向量积

给定空间的三个向量a,b,c,如果先做其中两个向量a,b的向量积a×b，再做所得向量与第三向量的向量积，那么最后的结果仍然是一个向量，叫做所给三向量的双重向量积，记做：(a×b)×c。

性质：

(a×b)×c=(a·c)·b-(b·c)·a

a×(b×c)=-(b×c)×a=(a·c)·b-(a·b)·c

关系式

给定空间内四个向量a、b、c、d，则这四个向量之间满足如下关系：

4f40494cda7d3374a00f74145ac21dd9.png

证明：

由混合积的性质可知

bb8904bce685f088c0432fd064cf4359.png


（即把c×d看成一个新的向量e，利用性质(a×b)·e=a·(b×e)）

再根据二重向量积的性质可知

fd7fea3324e64c638d303f6043a03cf1.png

该公式可用于证明三维的柯西不等式

400f64add34570289f841b17c4dee30b.png

证明：令公式中a=c、b=d，则：

5ccbf58e23480eac8a8a7b54271b9c97.png

设

54ce67c076497036f29bf5ccf68673d7.png


，那么：

2704c7032596b9b49a0c44df6505140a.png

即

400f64add34570289f841b17c4dee30b.png

等号成立的条件是

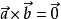
c4fb0fa6486062ef3f4591b48109e5f3.png


，即a、b共线（

96d228cfcd384bcc315e045c2761a6b7.png


或b=0）

两个向量构成的平行四边形的面积公式

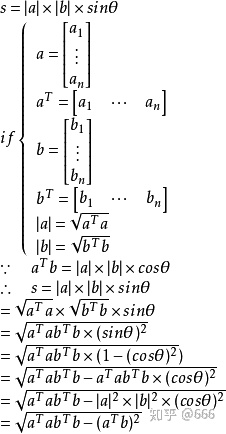
e1eecb87608cece12e2c8f2eca4ea1d9.png
向量空间模型(VSM)在文档相似度计算上的简单介绍
Felomeng的技术博客
03-25 4万+
C#实现在：http://blog.csdn.net/Felomeng/archive/2009/03/25/4023990.aspx向量空间模型（VSM：Vector space model）是最常用的相似度计算模型，在自然语言处理中有着广泛的应用，这里简单介绍一下其在进行文档间相似度计算时的原理。假设共有十个词：w1，w2，......，w10，而共有三篇文章，d1，d2和d3。统
向量数量积公式_向量的数量积公式大全
weixin_29090677的博客
12-24 1万+
学习数学需要讲究方法和技巧，更要学会对知识点进行归纳整理。下面是小编为大家整理的高二数学平面向量的数量积知识点，希望对大家有所帮助!高二数学平面向量的数量积知识点总结1.平面向量的数量积平面向量数量积的定义已知两个非零向量a和b，它们的夹角为θ，把数量|a||b|cosθ叫做a和b的数量积(或内积)，记作a·b.即a&m...积化和差，指初等数学三角函数部分的一组恒等式。可以通过展开角的和...
线性代数-向量空间
levin blog
09-09 5334
线性代数学习笔记向量空间 向量空间 向量空间的严格定义： 设 VVV 为一向量组，如果 VVV 非空，且 VVV 对于向量的加法以及数乘两种运算封闭，那么就称 VVV 为 向量空间。 所谓封闭，是指在 VVV 中向量进行数乘和加减，其结果依然在 VVV 中。具体的说，就是： 若 a∈V,b∈V,a \in V, b \in V,a∈V,b∈V, 则 a+b∈Va + b \in Va+b∈V 若 a∈V,k∈R,a \in V, k \in \mathbb{R},a∈V,k∈R, 则 ka∈Vka \i
向量空间模型 - 维基百科，自由的百科全书
09-23 492
向量空间模型 - 维基百科，自由的百科全书 向量空间模型 - 维基百科，自由的百科全书向量空间模型 维基百科，自由的百科全书 跳转到： 导航, 搜索 向量空间模型 (或者 词组向量模型) 作为向量的标识符（比如索引），是一个用来表示文本文件的代数模型。它应用于信...
向量的方向余弦公式_方向余弦怎么求
weixin_42118160的博客
02-05 3万+
励志语录(7qianxun.com)设：A(x1,y1,z1),B(x2,y2,z2)，向量AB的方向余弦＝｛(x2-x1)/d,(y2-y1)/d.(z2-z1)/d｝，其中，d＝|AB|＝√[(x2-x1)²+(y2-y1)²+(z2-z1)²]，(x2-x1)/d＝cosα.(y2-y1)/d＝cosβ.(z2-z1)/d＝cosγ，其中：α,β,γ是向量AB分别与x轴。y轴，z轴所成的夹角...
向量空间模型(Vector Space Model)
pennyliang的专栏
09-11 4741
向量空间模型(Vector Space Model)M个无序特征项ti ,词根/词/短语/其他每个文档dj可以用特征项向量来表示(a1j,a2j,…,aMj)权重计算，N个训练文档AM*N= (aij)文档相似度比较1)Cosine计算,余玄计算的好处是,正好是一个介于0到1的数,如果向量一直就是1,如果正交就是0,符合相似度百分比的特性,余玄的计算方法为,向量内积/各个向量的模的乘积.2
楔积与向量积1
08-03
向量积的模长等于两个向量构成的平行四边形的面积，而方向是通过右手拇指指向的那一个。 另一方面，楔积是代数中的一个概念，它用于多形式（Multiforms）的理论，特别是在微分几何和代数几何中。对于二维形式 **ω*...
py代码-输入两个包含若干整数的等长列表，把这两个列表看作两个向量， 输出这两个向量的内积。例如输入[1,3,5,7]和[2,4,6,8]，输出100。
07-14
向量的内积，也被称为点乘，定义为两个向量对应元素的乘积之和。在给定的例子中，我们将两个等长的整数列表视为二维空间中的向量，并计算它们的内积。 首先，让我们了解向量的基本概念。向量是由大小（或模）和方向...
两平面平行方向向量关系_线性代数总结 第三章 向量代数与几何计算（空间平面和直线）...
weixin_39682897的博客
12-22 5520
我的公众号“每日晴天”，可关注领取我的笔记pdf版哦~------------------------------------------------------------------------------一、向量1、简单的高中那些就不说了....2、左右手系：右手系：将右手四指(拇指除外)从x轴方向以小于π的角度弯向y轴方向，如果拇指所指的方向为z轴的方向，则称此坐标系为右手系。左手系：将左...
python定义向量内积_向量内积（点乘）和外积（叉乘）概念及几何意义
weixin_39633252的博客
12-05 3448
向量的内积(点乘)定义概括地说，向量的内积(点乘/数量积)。对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，如下所示，对于向量a和向量b： a和b的点积公式为：这里要求一维向量a和向量b的行列数相同。注意：点乘的结果是一个标量(数量而不是向量)定义：两个向量a与b的内积为 a·b = |a||b|cos∠(a, b)，特别地，0·a =a·0 = 0；若a，b是非零向量，则a...
两向量叉乘的计算公式_向量的叉乘运算法则
weixin_34632251的博客
01-13 2万+
向量的叉乘运算法则为|向量c|=|向量a×向量b|=|a||b|sin，向量的外积不遵守乘法交换率，因为向量a×向量b=-向量b×向量a。点乘和叉乘的区别点乘，也叫向量的内积、数量积。顾名思义，求下来的结果是一个数。向量a·向量b=|a||b|cos在物理学中，已知力与位移求功，实际上就是求向量F与向量s的内积，即要用点乘。叉乘，也叫向量的外积、向量积。顾名思义，求下来的结果是一个向量，记这个向量...
两个vector对应元素相加_2.3 vector
weixin_42510608的博客
01-26 3318
导图vectorvector是什么东东呢？就是它字面意思，向量。怎么理解呢？高中数学中我们学了能表示二维平面的中某一点的向量<x,y>,以及三维空间中表示某一点的向量<x,y,z>。到了大学，我们更加了解到<>中有多少个数字就能表示多少维度空间中的一点。c++借鉴并扩展了这个表示方法，用它来表示同种类型元素的聚集（我之所以不说是“集合”，是因为集合是元素不可重复...
向量
kakaxi123z的博客
10-11 1103
向量向量点乘 向量点乘 向量点乘的一些计算公式记录： 计算向量的长度： 向量的分量的平方后相加再开根号；比如 向量a（1，2，3） 12 +22+32=14 然后开根号 等于 3.74 那么 向量a的长度为：3.74 可用 |a| 表示向量的长度 计算向量单位化： 用向量/向量长度 2个单位向量可以用来表示两个方向，这两个方向可以进行比较（同方向还是不同方向）单位向量可判断方向 两个向量点乘： 结果是一个标量。如向量v1(1,2,3) v2(4,5,6)=4+10+18=32 公式 a * b =
向量空间模型
liixnhai的博客
06-29 3172
实数域定义向量 设有一个数的集合 F，它满足“F 中任意两个数的加减乘除法（除数不为零）的结果仍然在这个 F 中”，我们就可以称 F 为一个“域”。我们处理的数据通常都是实数，所以这里我只考虑实数域。而如果域 F 里的元素都为实数，那么 F 就是实数域。 如果 x1​，x2​，……，xn​∈F，那么 F 上的 n 维向量就是， 向量中第 i 个元素，也称为第 i 个分量。Fn​ 是由 F 上所有 n 维向量构成的集合。 向量中第 i 个元素，也称为第 i 个分量。Fn​ 是由 F 上所有 n 维向量构成的
向量空间模型(vector space model)
热门推荐
panjiao119的博客
10-17 3万+
向量空间模型(vector space model) 向量空间模型概念简单，把对文本内容的处理简化为向量空间中的向量运算，并且它以空间上的相似度表达语义的相似度，直观易懂。当文档被表示为文档空间的向量，就可以通过计算向量之间的相似性来度量文档间的相似性。文本处理中最常用的相似性度量方式是余弦距离。 VSM基本概念： （1） 文档(Document):泛指一般的文本或者文本中的片断(段落、句群
判断两个向量是否平行C++
最新发布
11-25
在C++中，判断两个向量是否平行（即它们的方向相同或相反）可以通过计算它们的点积（也称为内积）来完成。如果两个非零向量的点积为0，那么它们就是平行的。这是因为根据向量的性质，只有方向完全垂直的向量才会有零的点积。 以下是一个简单的C++函数示例，用于检查两个二维向量是否平行： ```cpp #include <iostream> // 向量类，包含x和y分量 class Vector2D { public: double x, y; // 构造函数 Vector2D(double x = 0, double y = 0) : x(x), y(y) {} // 计算向量的点积 double dotProduct(const Vector2D& other) const { return x * other.x + y * other.y; } }; // 判断两个向量是否平行 bool areParallel(const Vector2D& vector1, const Vector2D& vector2) { if (vector1.dotProduct(vector2) == 0 && vector1.x != 0 && vector2.x != 0) { // 检查不是零向量的情况 return true; } else if (vector1.x == 0 && vector2.x == 0) { // 如果都是零向量，则视为平行 return true; } else { return false; // 非零向量且不平行 } } int main() { Vector2D vec1(1, 0); Vector2D vec2(2, 0); // 示例：这两个向量是平行的 std::cout << "Are vectors parallel? " << (areParallel(vec1, vec2) ? "Yes" : "No") << std::endl; return 0; } ``` 在这个例子中，`dotProduct` 函数计算了两个向量的点积，而 `areParallel` 函数则使用这个结果来确定两个向量是否平行。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值