多元函数的向量表示_【凸优化笔记2】-凸函数、下水平集、范数

目录

1.凸函数

2.下水平集

3.范数

---

1. 凸函数

1.1 凸函数定义

一个函数

是凸的，如果定义域

是凸集，并且对于所有

，都有：

凸优化里对凹凸的定义和某些高等数学教材中对凹凸的定义可能正好相反，这里说的凸函数可能是某些高等数学教材中说的凹函数。
若

是凹的，则

是凸的。如图 1-1 所示为一个凸函数。

图 1-1

对上述凸函数

,若取

，

都有：

则称这个凸函数是严格凸的。

1.2 一阶条件

若

是可微（必定可导）的，则

是凸函数，当且仅当

的定义域是凸集且对

,都有：

表示

对

求一阶导数（梯度），当

时，

一阶条件可以简单表述为：

的切线总在

的下方，如图1-2所示。

图 1-2

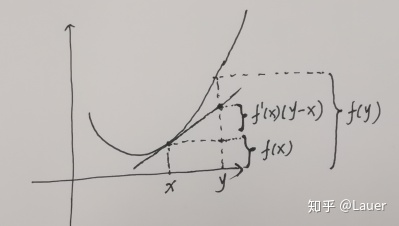
因此，对可微凸函数

,如果

,则

是极小值点。

1.3 二阶条件

若

是二阶可微的，则

是凸函数，当且仅当

的定义域是凸集且对

,

。

表示

对

求二阶导数（梯度），即

Hessian 矩阵，可用

表示，它是一个实对称矩阵。

（半正定矩阵）时

是凸函数，

（正定矩阵）时

是严格凸的。

关于矩阵正定的判定主要有以下三种方法：
1.矩阵特征值全大于0；
2.矩阵的n个顺序主子式全都大于0；
3.矩阵合同于单位阵；

2. 下水平集(sublevel set)

函数

：

的

下水平集定义为：

实质上就是一个函数满足一定条件时的定义域上的一系列点的集合(set)。level，水平的，指函数的取值，sublevel 即低于这个取值。
如：

，level 为

，set 为

的值小于等于

的所有点的集合。

凸函数的任意

下水平集都是凸集。而某个函数的下水平集都是凸集，但这个函数却不一定是凸函数（如：

）。

凹函数的

上水平集（将下水平集定义中的

改为

便得到上水平集）也是凸集。

下水平集的性质可以用来判断集合的凸性，若某个集合可以描述为一个凸函数的下水平集，或者一个凹函数的上水平集，则其是凸集。

3. 范数

3.1 范数的定义

满足以下条件的函数

:

称为范数：

• 是非负的：对所有
  ,都有
  ;
• 是正定的：仅对
  成立
  ;
• 是齐次的：对所有
  和
  ,都有
  ;
• 满足三角不等式：对所有
  ,都有
  ;

范数用符号

表示，范数是对向量

的长度的度量，我们可以用两个向量

的差异的长度来度量这两个向量之间的距离，即

,因此

也可以理解为向量

到原点的距离。

向量

和矩阵

的任意范数分别用

表示，而用带下标的范数来表示具体的范数，如将向量

的

范数定义为：

3.2 几个常用的范数

i.

范数

范数并非真正意义上的范数，一个向量的

范数等于向量中非零元素的个数。

范数是非凸函数。

ii.

范数

一个向量的

范数等于这个向量中所有元素的绝对值之和，即：

范数是凸函数，但不是可导的，如当

时

就不是一个可导函数。

iii.

范数

一个向量的

范数等于向量各个元素平方求和后再开根，即：

范数是凸函数，也是可导的。

iv.

范数

一个向量的

范数等于向量

中各分量绝对值最大时的取值，即：

v.

范数

范数是针对矩阵而言的，一个矩阵的

范数等于这个矩阵中所有元素的平方和的开平方根，即：

表示

中第

行第

列的元素。

表示矩阵

的迹，其含义是计算矩阵

的对角线所有元素之和。

对角线上第

个元素就是

第

行上所有元素的平方和。

矩阵的迹的一些性质：

，

。