面向地理大数据的新型密度山峰聚类算法（二）——各种聚类算法比较

整个研究分析的代码和文档我上传到GitHub上了：点击链接。

三、实验评估与分析

       本节对新型密度聚类算法（Clustering by fast search and find of density peaks）的聚类效果及其在相应数据库的性能表现，并与常用的聚类算法K-Means[3]、DBSCAN[2]和谱聚类算法[6]进行了对比分析，所有算法均由Python实现。

1. 实验数据和测试方法

1.1 实验数据

    对四种算法模型进行对比分析所采用的数据集共有10个，其中有人工数据集也有真实数据，包含7个带标签可用于参数评估的数据集和3个不带标签的数据集。所选的10个数据集十分具有代表性，涵盖了相连、内嵌、旋转、不同密度重叠和不同形状的情况，有一些是公认的分析聚类效果的常用标准数据集。

    其中，7个带标签的Aggregation[13]包括了7个飞告诉分布得聚类簇；Compound[14]包含了6个不同形状的复杂簇结构；D31[15]由31个高位密度簇组成； Flame[16]包含了两个相连的密度簇结构；Pathbased[17]包括了一个环形簇和两个内嵌的高斯密度簇；R15[18]由15个大小相似且相互重叠的的高位密度簇组成；Spiral[19]由三个相互缠绕旋转的条状密度簇构成。

    不带标签的3个数据集：t4.8k[20]由7个不同形状、互相嵌套且惨掺杂了大量噪声点的密度簇构；panelB[21]由5个不同形状且带大量噪声点的密度簇组成；MopsiLocations2012-Joensuu[22]是由Mopsi提供的用户位置分布数据。

                                                         

1.2 测试方法

        为验证算法的有效性，处于相同实验环境下，在Aggregation-t4.8k等7个基准数据集上测试了DBSCAN、谱聚类、k-means和Clustering by fast search and find of density peaks方法的聚类效果,评估方法采用与本文主要实现研究的新型密度聚类算法聚类结果相比较的方式。

       最终参与对比评估的聚类效果采用的是在多次实验中效果在最佳的一次，即和数据集标签类别最相近的。为验证算法的高效性和实际应用中的性能，还在MopsiLocations2012-Joensuu等数据集上测量了所提方法，评估了模型的效率和对输入参数的敏感性。

2 各算法效果评估

       在数据集上分别运行各个算法对比各个算法聚类的效果。各类算法参数阈值的选择遵循以下优先原则：（1）遵循原来算法默认最优值；（2）尽量采用相同参数：（3）多次试验聚类效果最优的参数值。

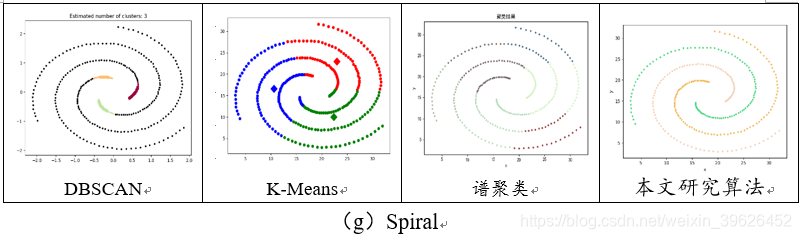
2.1 Aggregation-t4.8k等7个基准数据集聚类效果对比

2.3 模型评估

2.3.1 分群质量评估指标

对聚类效果的评估没有固定的标准，本文采用的是先使用sklearn库中提供的一些常用指标评价标准，然后在不同数据集下交叉验证不同群的分群指标。

（1）同质性：每个群集只包含单个类的成员

（2）完整性: 给定类的所有成员都分配给同一个群集。

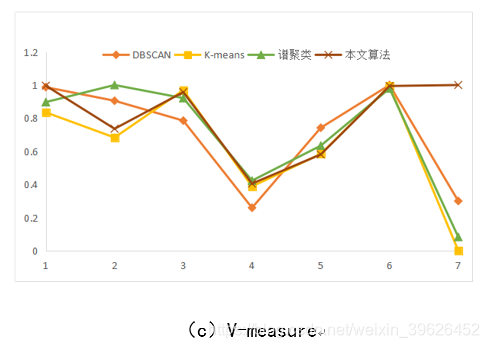
（3）V-measure：调和平均。

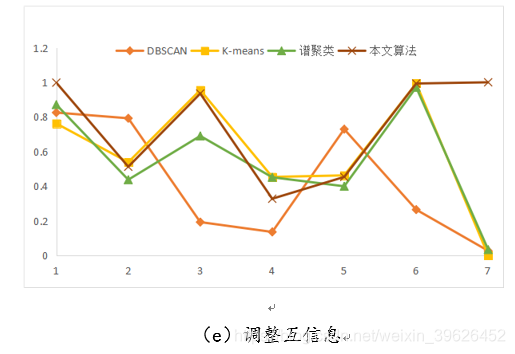
（4）调整兰德指数：整兰德系数假设模型的超分布为随机模型，即UU和VV的划分为随机的，那么各类别和各簇的数据点数目是固定的。调整的兰德系数为：

（5）轮廓系数：轮廓系数（Silhouette coefficient）适用于实际类别信息未知的情况。对于单个样本，设a是与它同类别中其他样本的平均距离，b是与它距离最近不同类别中样本的平均距离，轮廓系数为：

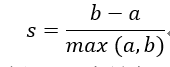
对于一个样本集合，它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数取值范围是[−1,1]，同类别样本越距离相近且不同类别样本距离越远，分数越高。

2.3.2 分析对比

如下图所示，为DBSCAN,K-means，谱聚类和本文研究算法在Aggregation等7个有标签的数据集下的各个评估指标对应值。

 

3. 评价结果

从聚类效果的对比图和各个量化评估标准的对比图可以看出，与传统的几类聚类算法相比，本文研究实现的新型密度山峰聚类算法具有的改进的优点：

1. 在K-means算法中，目标函数通常会是所有元素与一套假设出的聚类中心的距离之和，然后对其优化3-6次以求出那些最合适的聚类中心。然而，由于一个数据点总是分配到离它最近的中心，因此这种方法不能检测非球形的群，且聚类效果的好坏很大程度生取决于初值的选择和代表数据集的测试概率的可靠性。而Clustering by fast search and find of density peaks算法可以识别出非球形的群。
2. Clustering by fast search and find of density peaks算法只依赖于数据点之间的距离，计算简单，群的区分不依赖于它们的形状和所处的空间维度。DBSCAN算法将簇定义为汇集了相同的局部最大密度分布函数的点集。该方法可以分出非球形的集群但是只适用于坐标化的数据而且计算花费时间很长。
3. 群的数目直观可见、噪声点自动标出并排除在分析之外。在其它算法中需要人为地选取一个密度阈值作为“门槛”，对于密度值低于该“门槛”的数据点则视为噪声点，选择一个合适的“门槛值”是不容易的。

 存在的问题和不足：

1. 原文作者表明该方法对数据的量度变化有鲁棒性而不怎么影响到dc的取值，即公式（1）中密度估计值不变。显然，公式（2）中距离值会被这样的量值变化影响，但是很明显决策图的结构（特别是那些δ很大的数据点）是一个排名的结果密度值，而不是实际很远的点间的距离值。但在实际操作过程中，由于基于决策图的判断，dc会对聚类中心的选择产生很大影响从而影响聚类结构。
2. 该方法对于那些密度比较均匀，即没有密度山峰的数据集测试效果不佳。对于用来模糊聚类的测试集，由于本算法是基于密度这一原理，导致对分布太过均匀的数据点不能很好地识别出聚类中心。