两边同时取对数求复合函数_高中数学题型分析：对数运算

最新推荐文章于 2023-05-22 09:37:30 发布
最新推荐文章于 2023-05-22 09:37:30 发布
阅读量3.7k 收藏
点赞数
文章标签： 两边同时取对数求复合函数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_39628339/article/details/111684257
版权
本文详细介绍了高中数学中的对数概念、性质推导、运算训练及对数方程，强调理解“底数”、“指数”、“真数”的基础概念。通过大量的训练题，帮助学生巩固对数运算知识，为后续的函数学习打下基础。此外，还提及了对数在解析式中的应用，并推荐了两套题型训练资料供学生进一步练习。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

41620b33596561a0d7798ce0306a5c54.png

对数运算

对数，作为高中一个新的概念，对数运算也是新的运算内容，许多刚进高中的同学，常会受到对数概念的模糊与不清晰困扰，也为后续的指数函数与对数函数学习上，带上一定的影响，从而造成对高中函数理解的困难。

今天，我们同学对对数概念的引入、性质推导、运算推导，附加大量训练，希望对同学们在学习对数运算上有所帮助。

对数概念的引入

5ab9b3141da5521e4302992e9b6d5f18.png
fae5e2a512231c94a7b97a746d6f10bf.png

同学们，可以看看，以上是最基础的指数运算，而对数概念概念的出现，是为了解答指数中的指数幂而出现的一种运算，在这里同学们一定要把握“底数”、“指数”、“真数”的基础概念。

3168c1be66e884ffba26b445f28fbc74.png

对数符号“log”的引入，切记“log”为书写对数的符号，我们也可以看到，通过对数可以成功分析指数幂未知的情况，有点必须注意的是，对数是一个确定的值，有大小的区别。

其次，要注意2种特殊的底数，一种是以10为底的对数的表达形式，一种是以e为底的对数的表达形式，切记这两种表达以后都以lg、ln为标识，不需要换回的。

对数性质的推导

e1d6f279e0085d3ae099d6ecd5fbf6d3.png
ad247e425db372d9dbf7b39f0963963f.png

利用指数运算中的，特殊情况，分辨好“底数”、“指数”、“真数”的基础概念，为对数性质进行推导。

30493f56bd090275f0d0615b1bba8905.png

对数运算本质是一种运算，所以只要等式，两边同时取对数是成立的，所以随着性质的出现，我们可以推导出指数幂为对数形态的一条新的性质，这也是许多同学比较难理解，必须注重理解好“底数”、“指数”、“真数”的基础概念。

对数性质的训练

021e6d4901f05b51a7dfd0186ccc8ff9.png
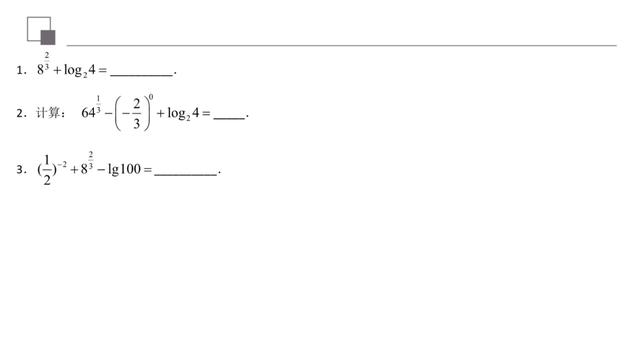
5afaaad09c96bc9afbf495107d644a08.png
6cc00c73a91f8b88152685e670e7eea2.png

对数性质的推导

aa264b40da0cc6e33e68b1b8601d8cd3.png
0deb10add97c2854026a7254656b8610.png

我们可以看到，对数运算性质，其实来源于指数运算的基础，所以，在理解对数运算的性质前提下，必须熟悉指数运算的内容。

847fe016302ce2088cbb1ae385eb677e.png
eda10e4596c2a98ecfeddc89728da3b7.png

利用指数运算另外两条性质，我们分析出新的两条对数运算性质。

对数运算的训练

b450df548ca7b3cad21b0a156f4268aa.png
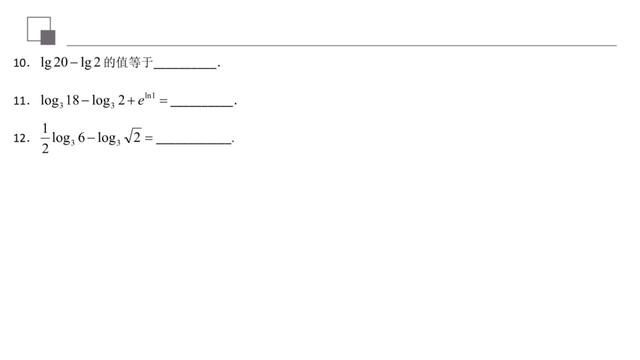
b1ab1626552f0c5fded552754b963d7c.png
72e2fe872aada2053e73fc6163b65845.png
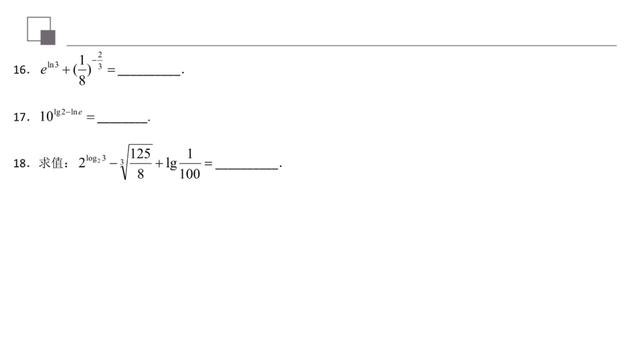
115cb6f6e355d4a993bc77e78df4415a.png
5ee1fcc3b743d6031e2de1d339db4465.png
873c256d14a8fc0d13b45c83467b045e.png
c8735c3a359f6b381d25ae0a198e6d84.png

通过对数运算的训练，同学们可以加强对对数概念与其运算的理解，解题过程一定必须注意概念的理解透彻，强化书写过程。

对数方程

9a6cf9f5bb465657a447e7950f1d7594.png
b8fd3f4739aafa2969f7cc5ea98a5b96.png
58e37330a6dba34f25860b1326475b71.png

我们可以看到，对数方程的解答方式有二种情况，其实大同小异，但第二种方法更加符合对数概念的理解与分析，强化逆用思维的训练。

对数方程训练

b062c97c6dcd151b484c7584ca7430e1.png
27ffbe1fd3f790284b74bc103731c283.png
158b77d79d146ffd3a1a6cb20b66c25c.png
d71f81d341a6e0beba53d4eaee24240d.png

通过对数方程的训练，我们更能强化对数运算的内容。

对数与解析式

26e68878df7cf0408f18a8213a2de98f.png
4c5066ce355a2c78eab0e9855dfdfc41.png

我们把对数运算放在了基础的解析式上，这样同学能学会开始如何把对数运算与解析式结合，也为后续的对数函数认知，提供了起点。

以上为高中数学题型分析：对数运算整节内容。

我们已经整理二套成熟的题型训练内容提供同学们进行训练，也欢迎同学们微信订购。

99c149c55e939c05cc0904b40f52786d.png
42bce95c9e78464e400c24c92419dd23.png
bf11dd644101708e2dc8664dbdfcc522.png

名称：高中数学初等函数题型分析。

页数：250页。

题量：802道。

销售方式：彩色纸质版邮寄。

价格：120元微信支付，包邮。

目录：总共22种题型

高中数学题型分析：乘方运算、整式乘除

高中数学题型分析：指数运算

高中数学题型分析：对数运算

高中数学题型分析：对数换底公式运算

高中数学题型分析：一次函数简单回顾

高中数学题型分析：二次函数简单回顾

高中数学题型分析：指数函数与对数函数图象

高中数学题型分析：一次函数与指对数函数定点

高中数学题型分析：指数函数与对数函数单调性

高中数学题型分析：指数函数与对数函数值域

高中数学题型分析：指对函数的大小比较

高中数学题型分析：反函数概念

高中数学题型分析：函数的解析式

高中数学题型分析：抽象函数的定义域

高中数学题型分析：函数奇偶性

高中数学题型分析：抽象函数的单调性和奇偶性

高中数学题型分析：幂函数

高中数学题型分析：函数的零点

高中数学题型分析：指数函数复合题型

高中数学题型分析：对数函数复合题型

高中数学题型分析：分段函数

高中数学题型分析：函数的对称性

70505ebc4d9ccf26a1d1a4b9ec21b0c8.png
def55d5cfe99141e2db8b44a52d6412e.png
055edf13a9b90c0c22b3e9a4a90d7223.png

名称：初高中数学衔接题型分析。

页数：226页。

题量：953道。

销售方式：彩色纸质版邮寄。

价格：120元微信支付，包邮。

目录：总共25种题型

初中数学题型分析：一元一次方程

初中数学题型分析：二元一次方程

初中数学题型分析：一元二次方程概念

初中数学题型分析：一元二次方程配方法

初中数学题型分析：一元二次方程开平方法求根

初中数学题型分析：一元二次方程判别式

初中数学题型分析：一元二次方程求根公式

初中数学题型分析：一元二次方程因式分解

初中数学题型分析：一元二次方程韦达定理

初中数学题型分析：分式方程

初中数学题型分析：不等式性质

初中数学题型分析：一元一次不等式

高中数学题型分析：集合的含义与表示

高中数学题型分析：区间理解

高中数学题型分析：集合的基本关系

高中数学题型分析：一元二次不等式

高中数学题型分析：集合的交集运算

高中数学题型分析：集合的并集运算

高中数学题型分析：集合的补集运算

高中数学题型分析：函数定义图象理解

高中数学题型分析：函数的定义域基础概念

高中数学题型分析：函数简单解析式分析

高中数学题型分析：函数的单调性证明

高中数学题型分析：函数的简单值域分析

高中数学题型分析：函数的奇偶性证明

两边同时取对数求复合函数_e2x求导(复合函数求导例题大全)
weixin_30122219的博客
02-05 5498
ln(ex +√(1 +e2x))'=1/[e^内x+√容(1+e^2x)]*[e^x+√(1+e^2x]'=[e^x+e^2x/√(1+e^2x)]/[e^x+√(1+e^2x)]==[e^x+e^2x/√(1+e^2x)]*[√(1+e^2x)-e^x]=e^x√(1+e^2x)-e^3x/√(.令2x等于t,e的t次方的导数等于e的t次方，2x的导数等于2，然后把两个求出来的导数相乘，等于2...
两边同时取对数求复合函数_初学讲义之高中数学七：对数
weixin_39612110的博客
12-22 3006
上篇已经讲了幂运算对于 ：a叫作底数，b叫作指数，N( 的结果)叫作a的b次幂。对数的定义当我们知道底数a和指数b，要求b个a相乘（a的b次幂）的值，进行幂运算就可以。那么当我们知道底数a和它的若干次幂N的值，要求指数b的值时该怎么办呢？这里就要引出对数运算了。对于已知底数a和它的幂N，倒过来求指数的运算叫作对数运算，这个运算（对数）记作 读作“以a为底N的对数”，在这里a依然叫作“底数”，N叫...
两边同时取对数求复合函数_等式两边同时取对数，什么条件下能同时取对数？？...
weixin_32098487的博客
01-17 7403
展开全部当等式一边出现指数的时候，等式两32313133353236313431303231363533e59b9ee7ad9431333431346435边可以同时取对数。等式两边同时取对数是为了便于对等式进行推理，运算。例如：1、已知y=(x+1)³(x-2)²，求导数。解：对等式两边同时取对数得：lny=3ln(x+1)+2ln(x-2)两边同时对x求导有：y'/y=3/(x+1)+2/(x...
两边同时取对数求复合函数_两种方法求函数y=(sinx)^(cosx)的导数
weixin_40005542的博客
12-23 2078
主要内容：本文通过对函数两边同时取对数，以及幂指函数变底方法，介绍计算y=(sinx)^(cosx)的导数的主要步骤。方法一：取对数法∵y=(sinx)^(cosx)∴lny=cosx*lnsinx,两边同时求导，则：dy/y=-sinx*lnsinxdx+cosx*cosxdx/sinx=(-sinx*lnsinx+cosx*ctgx)dx即：dy/dx=(sinx)^(cosx)*(-sinx...
两边同时取对数求复合函数_取对数求导法的例题 取对数求导法
weixin_32629285的博客
02-05 1万+
首先 自然对数 就是对e求对数 即ln 对数运算有几个规律 ln(x*y)=lnx lny ln(x/y)=lnx-lny ln(x^y)=y*lnx 这样一来 你应该就明白了吧 lny=ln{[(x^2)/(x^2-1)]*[(x 2)/(x-2)^2]^(1/3)} =ln(x^2)-ln(x^2-1) ln(x 2)^(1/3)-ln(x-2)^2^(1/3) =2lnx - ...什么是对...
同步精品课堂2019_2020学年高中数学第2章基本初等函数Ⅰ2.2.1对数与对数运算第2课时对数的运算练习新人教A版必修120
09-09
在高中数学中，对数是基本初等函数的一部分，它在数学分析、代数和几何等领域都有着广泛的应用。本节内容主要围绕对数及其运算展开，涵盖了选择题、填空题和解答题等多种题型，旨在帮助学生深入理解和熟练掌握对数的...
2022高中数学全程复习第三章第六节对数与对数函数.pptx
07-27
【对数与对数函数】 对数是一种数学概念，它在高中数学中占有重要的地位，尤其是在解决指数问题和方程求解中。对数的概念基于指数运算，如果一个数 \( a \) 的幂等于另一个数 \( N \)，即 \( a^x = N \)，那么数 \...
新疆乌鲁木齐市第一中学2015_2016学年高中数学2.2.1对数与对数运算练习无答案新人教版必修1
08-18
在高中数学课程中，对数与对数运算是基础知识点之一，尤其在新人教版必修1的教材中占有重要位置。对数运算不仅在数学领域广泛应用，它还是解决复杂问题的重要工具，在科学、工程乃至经济等领域都有其身影。掌握好...
高中数学对数和对数函数知识点与例题讲解.doc
09-30
高中数学中的对数和对数函数是核心概念，它们在解决复杂的数学问题中扮演着重要角色。对数是指数运算的逆运算，它允许...这些习题涵盖了对数运算、对数函数的性质、图像分析等多个方面，是提高高中数学技能的关键环节。
峨山彝族自治县高中数学第三章基本初等函数（Ⅰ）3.2对数与对数函数3.2.2对数函数导学案（无答案）新1.docx
10-22
3. **与对数函数相关的复合函数的单调区间**：例如，求`y=log_a (1-x)`的递减区间，需要结合复合函数的单调性和对数函数的性质来解答。 变式训练进一步巩固了这些概念，如通过解决课本上的练习题来深化理解。限时...
两边同时取对数求复合函数_高中数学：对数运算三难点
weixin_39548541的博客
12-22 1319
对数函数是重要的函数，自然也是高考的知识点，学习对数函数常会遇到一些难点，使解题思维陷入困境，归纳起来主要有三个方面。难点1 底数不统一对数的运算性质是建立在底数相同的基础上的，但实际问题中，却经常要遇到底数不相同的情况，碰到这种情形，该如何来突破呢？主要有三种处理的方法：(1)化为指数式对数函数与指数函数互为反函数，它们之间有着密切的关系：logaN=bab=N，因此在处理有关对数问题时，经常将...
什么情况下两边同时取对数
再来一下！
05-22 5507
如果a^x=N(a>0,且a≠1)，那么数x叫做以a为底N的对数（logarithm），记作记做x=log(a)(N)，其中a要写于log右下。解：根据题意,细胞每1小时分裂一次,分裂结果是一个细胞成为2个细胞，则100个细胞,1小时后成为200个,2小时后成为400个,依此类推,则n小时后是100×2的n次方；所以，y’=[3/(x+1)+2/(x-2)]*[(x+1)³(x-2)²]=3(x+1)²(x-2)²+2(x+1)³(x-2)两边同时对x求导有：y’/y=3/(x+1)+2/(x-2)
两边同时取对数求复合函数_对数正态分布
weixin_39624733的博客
12-19 1561
正态分布 对数正态分布（logarithmic normal distribution）是指一个随机变量的对数服从正态分布，则该随机变量服从对数正态分布。有些量本身就是不对称的。例如，试想，人们完成某项特定任务需要的时间：因为每个人都是不同的，我们会得到一个分布。然而，所有的值都必然是正数(因为时间不可能为负数)。而且，我们还能预测到该分布可能的形状：有一个无人可及的最小时间，然后是少数一些非...
计算机科学——高数
weixin_51535930的博客
11-05 259
函数的求导法则 高阶导数、参数方程导数、隐函数的求导 函数微分
回归什么时候怎么取对数_如何解读取对数(lg或ln）后的变量
weixin_29466045的博客
01-16 1万+
我们在读文献的时候，经常会看到变量取对数lg或者ln，那么这时候该怎么解读呢？为什么要讲这个呢？本周我们主任讲课的时候，讲到下面这个ppt，在这张ppt的第4条：采用年龄矫正：出生时为100%，每10年减10%。我看到这句话的时候冷了一下：没有想到弹性变量还真的会用到！以前我也搞不懂变量取对数，如lg(年龄)， 之后该怎样解读，后来我学习了计量经济学后，才搞懂了这个问题，相关资料大家可以...
二元函数对xy同时求导_高等数学期末总复习 DAY4. 利用莱布尼茨定理求高阶导 隐函数求导 对数求导法 参数函数求导等...
weixin_39614276的博客
11-21 1886
DAY 4.这世上总要有个明白人，懂得克制。DAY 4.1. 利用莱布尼茨定理求高阶导2.隐函数求导3.对数求导4.参数函数求导5.用导数求切线、法线6.函数的微分1. 利用莱布尼茨定理求高阶导只看两点： 1、常用导数的高阶公式2、例题例题2.隐函数求导这种方程里面y是x的函数，但是不显性。例题1 设 求 解：方程两边同时对x求导得 = 3.对数求导例题2 求 y 的一阶导解：方程两边同时取对数...
＜Zhuuu_ZZ＞HIVE(十一)函数
Zhuuu_ZZ的博客
09-22 2687
Hive内置函数一 Hive函数分类二 字符函数二 类型转换函数和数学函数三 日期函数四 集合函数五 条件函数六 聚合函数和表生成函数6.1 聚合函数6.2 表生成函数：输出可以作为表使用 一 Hive函数分类 从输入输出角度分类 标准函数：一行数据中的一列或多列为输入，结果为单一值 聚合函数：多行的零列到多列为输入，结果为单一值 表生成函数：零个或多个输入，结果为多列或多行 从实现方式分类 内置函数 自定义函数 UDF：自定义标准函数 UDAF：自定义聚合函数 UDTF：自定义表生成函数
为什么数据要取对数
热门推荐
fallenink的专栏
03-01 1万+
对这个问题，我转载了三篇文章： 作者：姚岑卓 链接：https://www.zhihu.com/question/22012482/answer/21315349 来源：知乎 著作权归作者所有，转载请联系作者获得授权。 如需要收回，还请联系我，会将其删除，只保留导流的连接 对数据做一些变换的目的是它能够让它符合我们所做的假设，使我们能够在已有理论上对其分析。 对数
基于Retinex模型与多尺度融合的低光照图像增强算法及其应用
最新发布
04-28
内容概要：本文介绍了一种基于Retinex模型和多尺度融合的低光照图像增强算法。首先，通过对原图像进行光照图分解并利用Retinex模型进行估计，再经过伽马矫正获得亮度均衡的图像。接着，为补偿伽马矫正当中的过曝细节丢失，进行了锐化处理以提升图像细节。最后，在多尺度融合金字塔模型下，根据不同输入图像的权重进行融合，从而得到最终的增强图像。文中还详细介绍了五个非参考图像质量评价指标（BRISQUE，CEIQ，ENIQA，NIQE，PIQE），用以评估算法的效果。 适合人群：从事计算机视觉、图像处理领域的研究人员和技术人员。 使用场景及目标：适用于需要在低光照条件下获取高质量图像的各种应用场景，如安防监控、自动驾驶、医疗影像等领域。目的是提高图像的亮度、对比度和细节，确保后续图像处理任务的有效性和准确性。 其他说明：该算法不仅提高了低光照环境拍摄照片的质量，也为其他计算机视觉应用提供了更好的图像素材，具有重要的社会和经济价值。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值