两边同时取对数求复合函数_取对数求导法的例题 取对数求导法

首先 自然对数 就是对e求对数 即ln 对数运算有几个规律 ln(x*y)=lnx lny ln(x/y)=lnx-lny ln(x^y)=y*lnx 这样一来 你应该就明白了吧 lny=ln{[(x^2)/(x^2-1)]*[(x 2)/(x-2)^2]^(1/3)} =ln(x^2)-ln(x^2-1) ln(x 2)^(1/3)-ln(x-2)^2^(1/3) =2lnx - ...

什么是对数求导法? 作为一种求函数导数的方法,对数求导法应用相当广泛。一些常用函数(比如幂函数)的导函数公式可以用它来推导出来。 对于要求导的函数,如果直接运用定义不方便推出其导数,可以对其两边取对数(一般取自然对数),注意对y作...

y是关于x的函数lny相当于复函数,求导则为(lny)'乘y'=(lnx)',开出来就是了。 主要是lny是关于y的函数,y是关于x的函数,理解就好了。

是这样的: “两边分别求导”这句话省略了两个字,应该是“两边分别对x求导”. 如果:lny对y求导,当然是1/y,但是,现在是对x求导,这里由于y是x的函数,所以应用复合函数的求导法则,先求出lny对y的导数1/y,然后乘以y对x的导数y',即lny对x的导数...

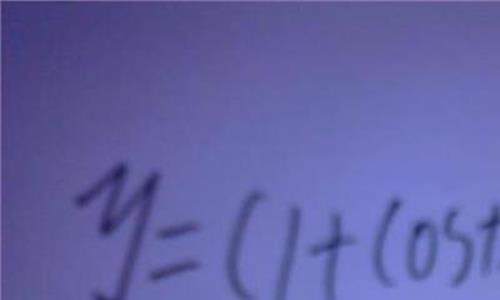
(ln

x

)'=1/x 这是基本公式, 推导如下 (lnx)'=1/x [ln(-x)]'=1/(-x)·(-x)' =1/x ∴ (ln

x

)'=1/x

取了对数之后,左右两边都变成了新的复合函数,如左边变成 u = lny, y = lnx 这样的复合关系。 求导时,自然从最外层的函数关系求导,得到 1/y. 因为是对x求导,y仍然是x的函数,所以还得继续再导一次,得y'。综合起来就是相乘,即:(1/y)*y'。 ...

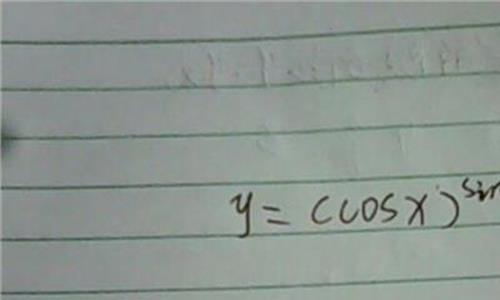
对数求导公式为 (Inx)' = 1/x(ln为自然对数) (logax)' =x^(-1) /lna(a>0且a不等于1) 你贴出来的题目不是对数求导。 原式=1/2(xsinx(1 e^x))^(-1/2) * ((sinx cosx)(1 e^x) e^x(xsinx)) 打字关系,根号只能用指数^符号表达。 复合函数的求导意...

已经提醒用对数求导法:取对数 lny = sinx*lnx, 求导,得 y'/y = cosx*lnx sinx/x, 故 y' = y(cosx*lnx sinx/x) = ……。