c++求矩阵的秩_线性代数复习(被玩坏的矩阵)

最近, 老有同学问, (线性)代数应该怎样复习呀. 本期就来谈谈我对这门课程的看法, 希望对大家有所帮助. 

线代故事梗概大家不妨回想一下之所以有这门课程的「罪魁祸首」是什么? 那当然是  线性方程组

如果没有线性方程组, 就没有这门课程. 

当然有人会说, 中国人在上千年前的《九章算术》中已经解释了怎么解线性方程组了, 为什么到近代才有线性代数呢? 是的, 如果我们只想知道线性方程组的解是什么, 《九章算术》就已经告诉我们解法了, 就是我们课本里提到的Gauss消元法. 这个方法用的就是矩阵的方法. 

从字面上讲，感觉「方程」跟「矩阵」好像差不多是一个意思. 

但是, 如果仅仅是将一些数字整齐的排在一起做一些初等行列变换, 这个矩阵好像也没有什么好玩的. 

下面我们就来看下矩阵(方程)是怎样一步步被「玩坏」的. 

矩阵乘法   这是矩阵变得「好玩」的最「刻骨铭心」的时刻. 矩阵有了「乘法」后，一切都变得不同了. 

初等行变换可以看成在矩阵左边乘以相应的初等矩阵; 

可以玩可逆矩阵, 以及可逆矩阵的各种刻画，如: 它们正好是初等矩阵的乘积; 方阵可逆当且仅且秩与阶数相等. 

还可以利用初等变换求可逆矩阵的逆矩阵. 

行列式   方阵 A的行列式是否为零可以用来判断相应的线性方程组 Ax = 0是否只有只唯一解. 

矩阵乘积的行列式等于它们行列式的乘积. 这使得矩阵乘法的问题和行列式的问题有时候可以相互转化. 

比如: 可逆的矩阵行列式一定非零, 反过来也成立, 实际上, 如果A的行列式非零, 它的逆矩阵可以用它的伴随矩阵写出来 

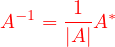
系数矩阵可逆的线性方程组的克莱姆规则是用矩阵行列式描述的. 

向量空间   向量空间的出现进一步丰富的矩阵的玩法. 

向量空间与矩阵的相互转化关系是这样的. 取n维向量空间V 的一组基, 对于V 中向量组 α₁,⋅⋅⋅,α_m, 分别取它们在这组基下的坐标A₁,⋅⋅⋅,A_m, 将它们拼在一起组成矩阵A. 

原向量组的问题可转化为矩阵A的问题. 例如: α₁,⋅⋅⋅,α_m线性无关, 当且仅当线性方程组Ax = 0只有零解, 当且仅当A的秩是m. 

要寻找α₁,⋅⋅⋅,α_m的极大线性无关组也可以从矩阵A来考虑, 可对A进行初等行变换(就像Guass 消元法一样), 将A变为A′ = [A′₁,⋅⋅⋅,A′_m]. 这时, 与A′的列向量的极大线性无关组对应的α₁,⋅⋅⋅,α_m中的向量就组成其极大线性无关组. 

由于最常见的向量空间是像ℝ^m这样的空间, 它里面的每个向量都是m个实数的一个序列. 如果把n个这样的向量排成n列, 我们就得到一个m行n列的矩阵. 

矩阵和向量空间的还有一个重要的联系是: 假设A是一个n列的矩阵, 齐次线性方程组Ax = 0的所有解组成一个向量空间, 称为Ax = 0的解空间, 记为Ker(A). 我们知道 

dim Ker(A) = n−rank(A)

一个矩阵的秩的看法也变得更加丰富: 假设 A是一个 m行 n列的矩阵.  A的秩有下面几种看法: 

1. 如果A可以通过初等变换变为(i,i), i = 1,⋅⋅⋅,r为1, 其余位置全为0 , 那么rank(A) = r. 

2. 如果A为非零矩阵, A的秩等于A的非零子式的最大阶数. 

3. A的秩可以看成其所有列(或者行)组成的向量组的最大线性无关组的向量个数. 

4. A的秩可以看成其所有列(或者行)生成的向量空间的维数.

线性变换   线性变换是一个向量空间 V 自己到自己的保持线性组合的映射 σ. 取定向量空间 V 的一组基, 考虑 σ在这组基下的矩阵. 这样 σ的问题同样可以转化为矩阵 A的问题. 

当然这里取不同的基, 得到的矩阵不一样(但它们彼此相似). 寻找那些相对简单的矩阵, 即相似标准型的艰辛过程成了这一章的主要内容. 

用到的方法主要还是矩阵和线性方程组. 如: 方阵A的特征值和特征向量, 分别是求 

f_A(x) = |xI −A|的根 λ和解线性方程组  (A−λI)x = 0如果要完全读懂这一部分的内容, 需要很花费一番功夫. 

详情参见: 相似标准型导读

二次型   由于矩阵实在是「太好玩」了, 因此近代以来很多数学问题都试图转化为矩阵的问题来解决. 比如二次型就是这样一个典型例子. 

本来二次型的样子是这样的 

q(x₁,x₂) = 2x₁² + 3x₂² + 4x₁x₂但在那些「挖空心思」想玩矩阵的眼里是这样的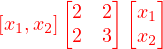  这样这个二次型的所有信息都包含在中间这个对称矩阵里了. 

用线性替换将二次型化为只有平方项的形式, 等价于将中间矩阵合同到一个对角矩阵. 

这里有个巨大的「坑」需要注意: 实对称矩阵合同到对角矩阵欧氏空间中有别的办法. 

对于一个实对称矩阵A, 如果要求找一个正交矩阵U使得U^TAU是对角矩阵, 不能用这里初等变换的方法. 

欧氏空间   欧氏空间 V 是实数 ℝ上的向量空间，同时有一个内积  (−,−) : V ×V → ℝ它是双线性, 对称, 正定的. 

有了这个内积, 我们在初等数学中学到的向量的内容都可以在欧氏空间中实现: 向量长度, 两个向量夹角, 垂直等等. 

欧氏空间上保持向量长度的线性变换无疑是我们最感兴趣的. 这样的线性变换称为正交变换. 

我们同样希望将正交变换的问题转化为矩阵的问题. 但由于正交变换是一种「来之不易」的变换, 它配得一上种「漂亮」的矩阵. 如果我们随便找一组基, 再考虑正交变换在这组基下的矩阵的话, 会有「暴殄天物」的风险. 

最终，我们发现，如果为欧氏空间找一组像直角坐标系那样的基: 相互正交且都是单位向量, 称为规范正交基, 那么正交变换在规范正交基下的矩阵就是正交矩阵, 即满足U^TU = I的实数矩阵. 

沿着这个方向，你会问: 怎样找一组规范正交基? 答案就是 Schmidt 正交化方法. 

怎样找出或者判断正交矩阵? 只要矩阵的列向量组成规范正交基即可. 

欧氏空间中, 还有一种重要的线性变换是对称变换. 它在规范正交基下的矩阵是实对称矩阵. 

对称实矩阵A有个很重要的特点是, 存在一个正交矩阵U, 使得U^TAU  = Λ是一个对角矩阵. 注意到此时U^T = U⁻¹, 因此A与Λ既是相似, 又是合同. 

怎样寻找这样的U? 从书中找找答案吧. 

要注意和实二次型那里的方法对比, 看看这两者的区别. 

线代「硬核科技」

如果要评选线性代数中最「基本」, 最「硬核」的技术, 我想应该选下面两个, 这两个基本知识不掌握熟练, 线性代数不可能学得好. 

1. Gauss 消元(加减消元)法. 

2. 线性方程组Ax = b的解的结构. 

特别是齐次线性方程组Ax = 0的基础解系. 

从上面的梗概可以看出, 几乎所有的问题都与这两个知识相关. 

「矩阵」的看法假设 A是一个 m行 n列的实数矩阵, 在不同的场景下，我们通常需要以不同的视角来看待 A. 

1. 在解线性方程组Ax = b时，我们把A和b拼在一起形成线性方程组的增广矩阵(A,b), 然后对这个增广矩阵做初等行变换. 这是我们看A最普通的视角: mn个数字排在一起. 

2. 有时候我们需要把A看成是列(或者行)向量拼在一起. A的列向量都是ℝ^m中的向量, 它们的所有线性组合组成ℝ^m的一个子空间, 称为A的列空间, 记为Col(A); 

类似的, A的行都可以看成ℝⁿ中的向量, 它们的所有线性组合组成ℝⁿ的一个子空间, 记为Row(A). 

这时A的秩rank(A)与其列空间和行空间的维数相同. 这样就可以把向量空间的方法用来解决与矩阵秩相关的问题. 

比如: 如果B是另外一个矩阵且BA = O, 要求证明 

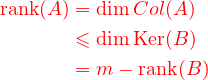
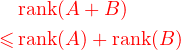
rank(A) + rank(B) ≤ m这时, 如果将 A看成若干个列向量拼起来的, 我们就很容易看出 A的列向量都是齐次线性方程组 Bx = 0的解, 从而 Col( A)包含在 Bx = 0的解空间Ker( B)中. 因此  伙伴们, 如果 B也是 m  ×  n的矩阵，说明下 

或者B是一个m行的矩阵, 证明下 

(提示: 矩阵的秩等于其列向量组的最大线性无关组的向量个数) 

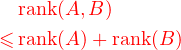
3. 当然, 还有的时候我们要将方阵A看作线性变换, 它将α映为Aα. 

最后几点tips线性代数的特点是:  概念多, 概念之间关系复杂. 任何试图在几分钟之内掌握所有知识点都是徒劳的. 如果想要比较好的掌握这些知识, 比较有效的办法是. 

1. 分章节列出各个知识点, 以及这些知识点之间的关系图. 

2. 针对每个知识点, 举1-2个例子或者例题来理解这个知识点. 

3. 做适当的练习题，特别是证明题, 增加对知识点的应用能力. 

4. 最后, 记得我们的宗旨: 尽量把问题转化为矩阵和线性方程组的问题.