指数随机变量 泊松过程跳_足球比赛的进球规律-泊松分布

本文重点解读足球比赛与进球相关的数据。

通过数据分析发现：

• 欧洲职业足球比赛场均进球数为2.71个（2008/09至2015/16赛季）。
• 欧洲职业足球比赛确实存在主场优势：主队获胜占46%，客队获胜占29%。
• 最常见的比分是1:1。
• 足球比赛进球数服从泊松分布。
• 职业足球比赛的场均进球数过高或者过低都会损害其魅力。

泊松分布

离散型随机变量

的所有可能取值为0，1，2，...，且取各个值的概率为：

其中

为常数，则称

服从参数为

的泊松分布。

另，

为事件出现的期望值。

验证足球比赛进球数是否服从泊松分布的步骤

1. 利用泊松分布模型对足球比赛的进球数数据进行拟合，得到对
   的估计。事实上，这一过程相当简单，因为由概率论与数理统计的知识可以知道，对
   的估计就是场均进球数。所以第一步就是计算场均进球数。
2. 利用泊松分布模型和场均进球数，计算出进球数的理论计算分布。
3. 比较实际数据与理论计算分布，如果非常接近，就说明足球比赛的进球数分布服从泊松分布。结果如下。

主队进球数分布

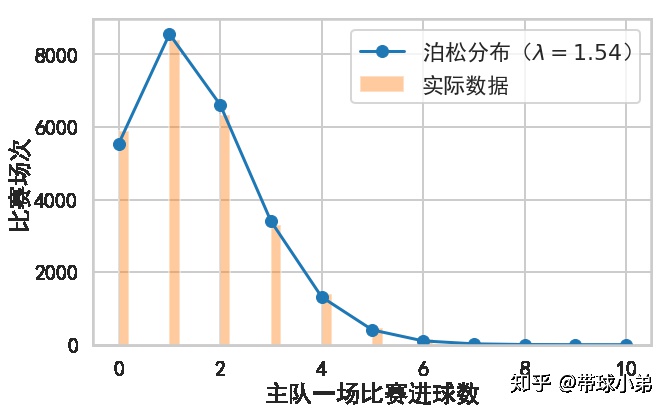
客队进球数分布

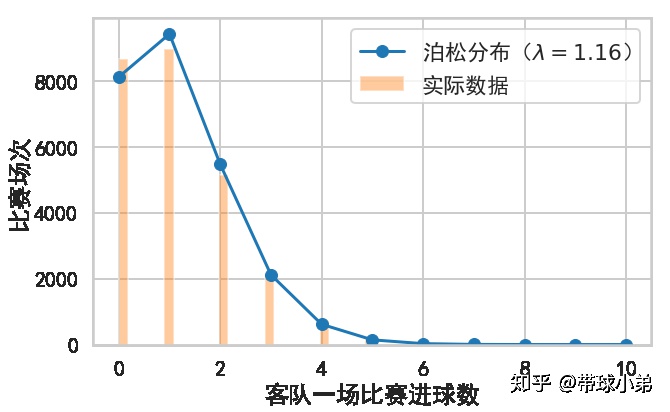
从以上两个结果可以知道，足球比赛进球数确实服从泊松分布。

下面利用泊松分布进行推广计算。

总进球数分布

总进球数也应该服从泊松分布。这是因为：主队进球数 ~

，客队进球数 ~

，所以总进球数 ~

（详细推导过程请查看链接）[1]。

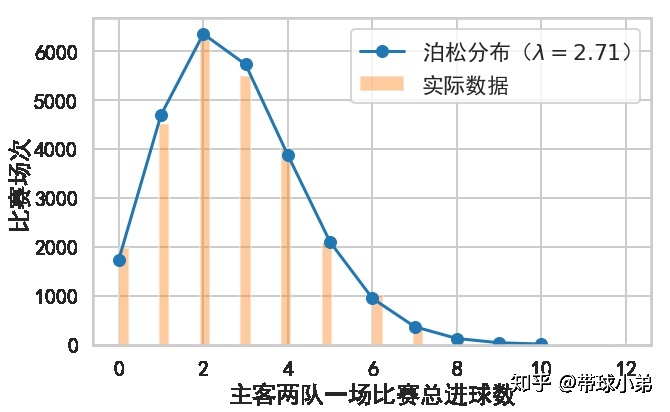
主队与客队之间的净胜球分布

因为主队和客队的进球数服从泊松分布，由理论推导可知，两队的净胜球数服从skellam分布（详细推导请参看链接[2] [3]）。

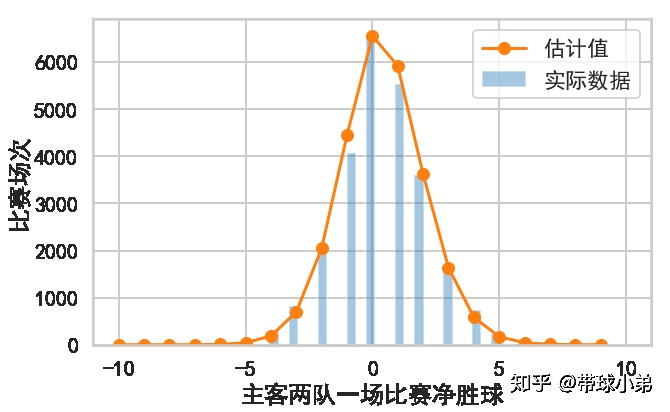
比赛胜平负比例

利用泊松分布模型和场均进球数还可以预估出足球比赛胜平负的总体比例：

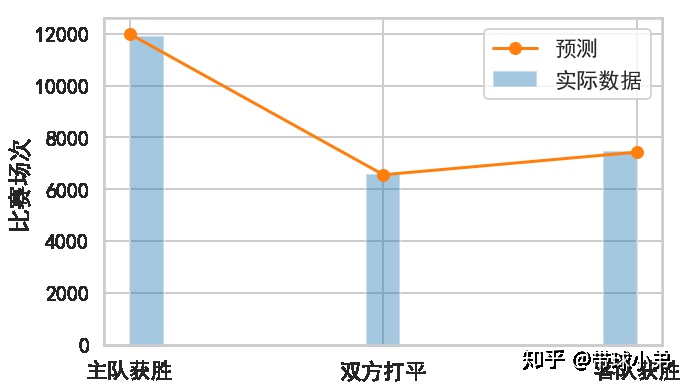
预测的比例和实际比例非常接近。

另外一个从图中可以得到的结论是：主队获胜占46%，双方打平占25%，客队获胜占29%。这表明欧洲职业足球比赛确实存在主场优势。

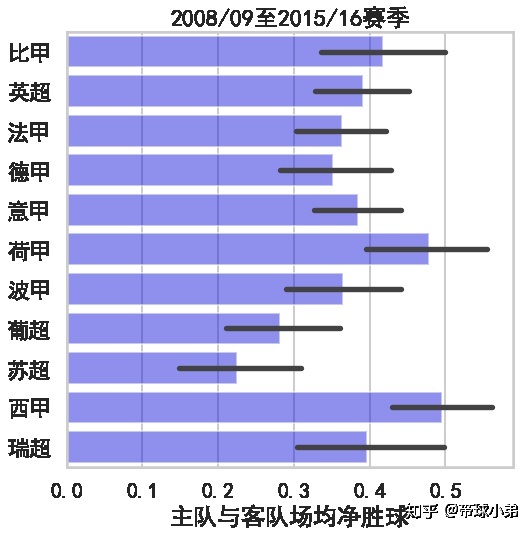
从下图也能得到同样的结论。在所有11个欧洲职业联赛中，主队的场均进球数都要比客队多。这表明，主场优势是普遍存在的。

各种比分出现的比例

利用泊松分布模型和场均进球数还可以估计各种比分的出现比例（区分主客队，主队在前，客队在后。比如，1:0代表主队1:0客队，0:1代表主队0:1客队）。

预计最常见的10种比分为：

比分 | 估计比例

1:1 11.98%

1:0 10.32%

2:1 9.26%

2:0 7.97%

0:1 7.76%

1:2 6.96%

0:0 6.68%

2:2 5.37%

3:1 4.77%

0:2 4.50%

实际最常见的10种比分为：

比分 | 出现比例

1:1 11.60%

1:0 10.17%

2:1 8.39%

2:0 8.21%

0:0 7.61%

0:1 7.17%

1:2 6.39%

2:2 5.04%

3:1 4.64%

0:2 4.64%

理论估计和实际情况非常一致。在当前场均进球数的情况下，足球比赛最可能出现的比分是1:1，其次是1:0，然后是2:1和2:0。

由以上的分析可以知道，足球比赛的进球数确实服从泊松分布。这样的规律广泛适用于所有的足球比赛，而不限于欧洲足球比赛。只要我们知道了某一个联赛或者杯赛的场均进球数这一数据，我们就能利用泊松分布和场均进球数估计出所有比赛的进球数分布、比分分布和比赛结果分布。

场均进球数

某种程度上说，足球比赛的场均进球数定义了其魅力。进球率过高或者过低都会损害足球的魅力。

假设足球比赛的进球率变低：主客两队每场比赛平均只能打进0.8球，即总场均进球数为1.6。则由泊松分布可以计算出此时各种比分出现的可能性为：

比分 | 估计比例
0:0 20.19%
0:1 16.15%
0:2 6.46%
0:3 1.72%
1:0 16.15%
1:1 12.92%
1:2 5.17%
1:3 1.38%
2:0 6.46%
2:1 5.17%
2:2 2.07%
2:3 0.55%
3:0 1.72%
3:1 1.38%
3:2 0.55%
3:3 0.15%

此时0:0出现的可能性最大，占到了所有比赛的1/5。每场比赛最多能看到两个进球的概率为78%。进球率过低会使得0:0的比赛变多，没有进球比赛就变得乏味，相信这样进球率的“足球”不会有太大的吸引力。

另一方面，进球率过高会使得强队获胜的可能性增大。

假设强队场均进球率为1.5，弱队进球率为1。由泊松分布计算出此时比赛胜平负的比例为：

强队获胜概率估计：48.79%

双方打平概率估计：25.98%

弱队获胜概率估计：25.22%

当进球率提高1倍后，强队场均进球率为3，弱队进球率为2。此时比赛胜平负的比例为：

强队获胜概率估计：58.53%

双方打平概率估计：16.77%

弱队获胜概率估计：24.70%

可以看到，进球率过高，会使得强队获胜的可能性增大，弱队爆冷的可能性降低，比赛变得没有悬念。
因此，职业足球比赛的场均进球数控制在2~3之间是一种非常精妙的设计，这样的进球率是职业足球的独特魅力之所在。

技术说明

• 详细数据分析过程（含代码）：足球比赛的进球规律。