小波变换理解

假定我们的原始信号为一个时域信号，我们经过任何数学变换的方式进行变换的信号就变成了一个经过处理的信号，继而我们可以在从处理后的信号中获取原始信号无法直接体现的信息。

变换的方法有很多，傅里叶变换是目前最流行的变换方法。利用傅里叶变化，我们可以得到信号的频谱。我们所知道的大多数情况中，信号的频率中包含着重要的信息。而信号的频谱就是信号的频率组成，可以显示出信号中存在怎么的频率。

自上到下：原信号、原信号频谱

我们可以看到的是，傅里叶变换给出了信号中存在何种频率分量的信息，也就是说告诉我们了信号的各种频率的个数，但我们也可以发现，傅里叶变换后信号中不存在时间信息，它没办法告诉我们特定的频率在何时存在。

当我们需要知道信号中的频率分量的时间定位信息时，我们会更希望获取到（时间-频率）的信息转化方式。获取信号的时间-频率表示 的方法有不少，这里主要讲一下短时傅里叶变换short time Fourier transform和小波变换，而小波变换的出现其实是为了优化短时傅里叶变换。

短时傅里叶变换（Short Time Fourier Transform, STFT）是一个主要用于语音信号处理的通用工具，实际上计算短时傅里叶变换的过程是把一个较长的时间信号分成相同长度的较短的信号段，在每个较短的信号段上去计算傅里叶变换。

基本思想：把非平稳过程看成是一系列短时平稳信号的叠加，短时性可通过在时间上加窗实现。。通过该方法，人们至少可以说，无论发生了什么，它一定是发生在信号的某个特定部分。

短时傅里叶变换通常定义为

其中

在我们实现STFT时，其实是被计算成一系列加窗数据帧的快速傅里叶，其中窗口随时间滑动

来看一下STFT的具体操作步骤。

现在的数据如下分别对应着100hz，300hz以及100Hz+300Hz混合，这个时候我们选取中间频率，也就是150Hz作为一个截止频率，配置一个150Hz的低通滤波器和一个150Hz的高通滤波器，就可以得到频率范围为0-150Hz与150Hz以上两种情况，如下图

自上到下：原信号、0-150频域、150频域以上

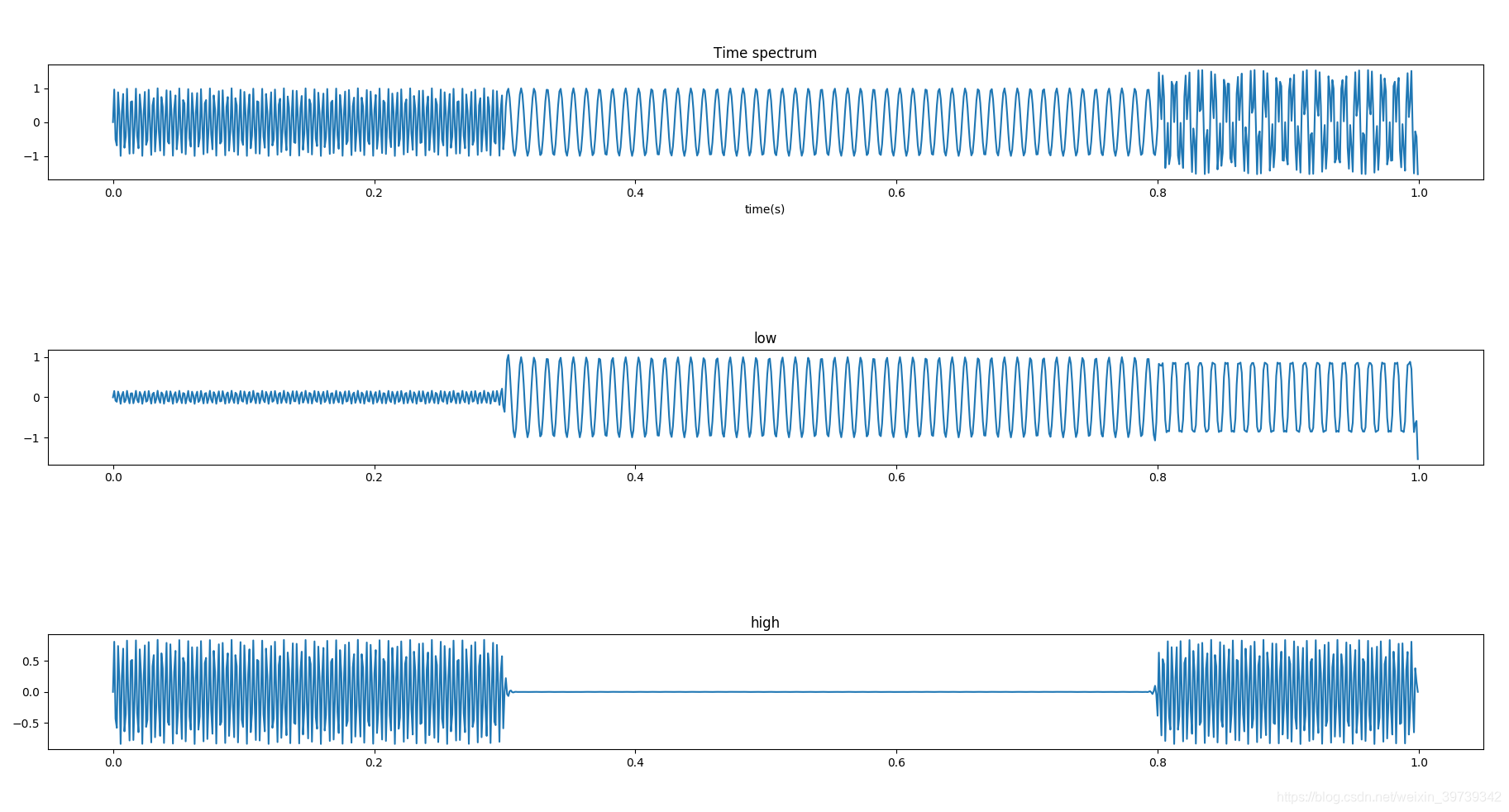
如果我们再细分，利用两重滤波器，也就是150Hz的低通滤波器搭配75Hz的高通通滤波器（其实也就是75-150Hz的带通滤波器），就能实现更低的频率范围

如下图，频率范围分别是0-75,75-150,150-225,225以上

自上到下：原信号、0-75频域、75-150频域、150-225频域、225频域以上

所以重复这样的操作，知道把信号分解到一定的预定义水平，我们就得到一组信号，表示这组信号的不同频率在不同时间出现的情况，我们将这种做法成为分解，而我们最终的预定义水平的频率范围称为STFT的分辨率。这里要提一下不确定性原理，原理表明的是一个粒子的位置和动量不能同时知道，用在这个地方也即说明了我们不能准确知道某个频率存在哪个时间点，但我们可以知道某个时间段时，存在着哪些频率范围。

自上到下：原信号、STFT后

接下来调用了scipy.signal.stft()进行短时傅里叶变换，我们就可以发现一个问题，STFT分解波时的分辨率是固定的，这对我们实际的研究是不实际的，所以小波分析很好的解决了这个问题。

小波变换给出了可变的分解间隔：高频信号按时间分解，低频信号按频率分解。

对于高频，相同时间段内，其样本更多，因此，样本间时间间隔也就越短。换句话说，高频信号可以按照时间进行分解。而对于低频，相同时间段内，其样本很少，因此，低频信号并不能很好的按照时间分解。

其实可以简单理解成，低频信号按照频率定位更好，频率之间的间隔随着频率的增加而增加。

自上到下：原信号、STFT后、小波变换后