文章介绍
全文配图,便于理解,严谨推导放在最后。
提前说明关键步骤:
推导第一定义时:将两条焦半径利用切线长定理转换为到圆锥面两点距离。
推导第二定义时:将焦半径和到准线的距离利用垂直条件转化成圆锥轴线长。
文章分为六个部分:
一、圆锥曲线,圆锥曲线的定义。
二、圆锥曲线的第一定义与“圆锥”曲线。
三、圆锥曲线的第二定义与“圆锥曲线。
四、圆锥曲线的一般性质。
五、上述一~四的过程推导。
一、圆锥曲线[1]
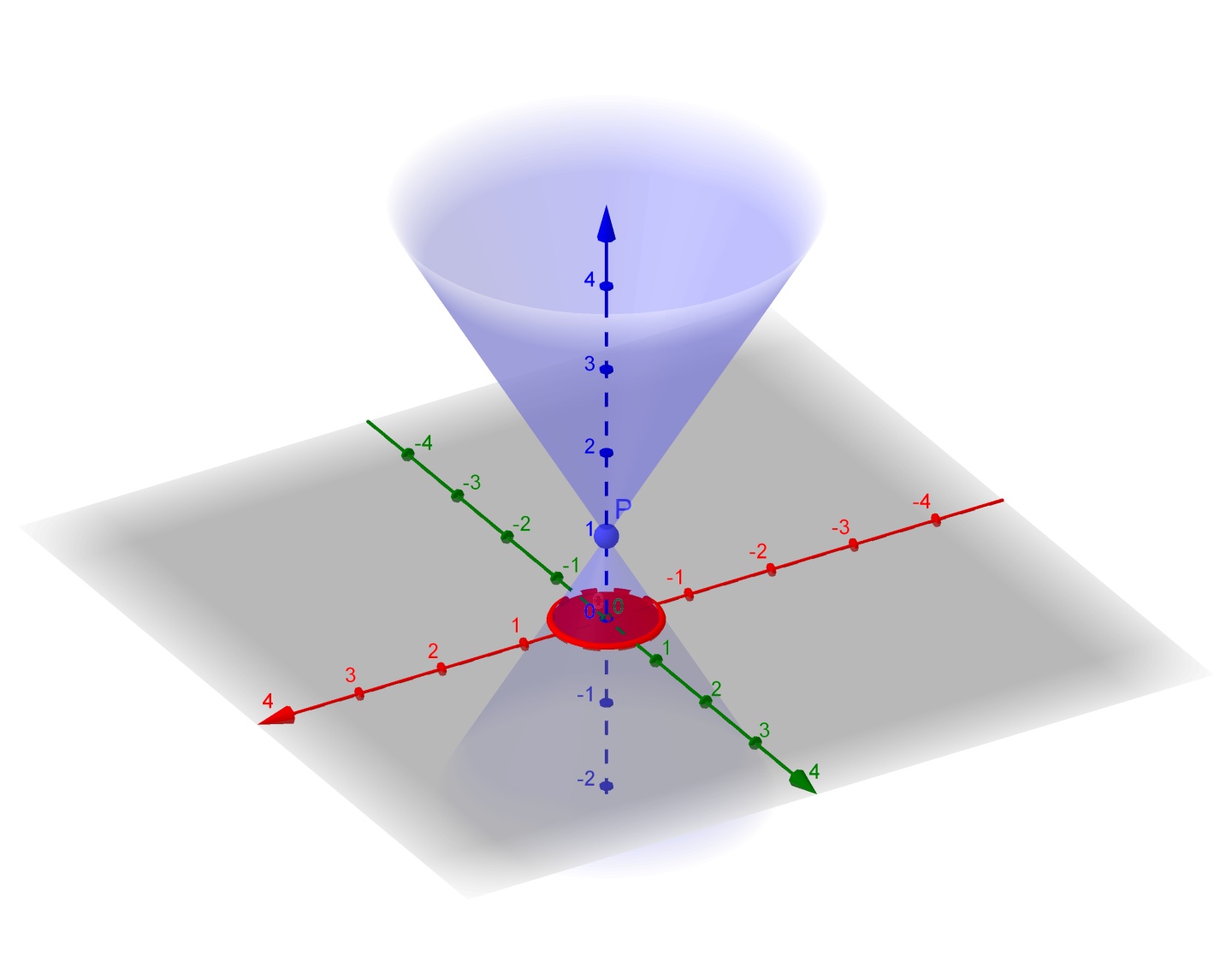
圆锥曲线,是由一平面截二次锥面得到的曲线。圆锥曲线包括椭圆(圆为椭圆的特例)、抛物线、双曲线,在笛卡尔坐标系中全部为二次曲线。
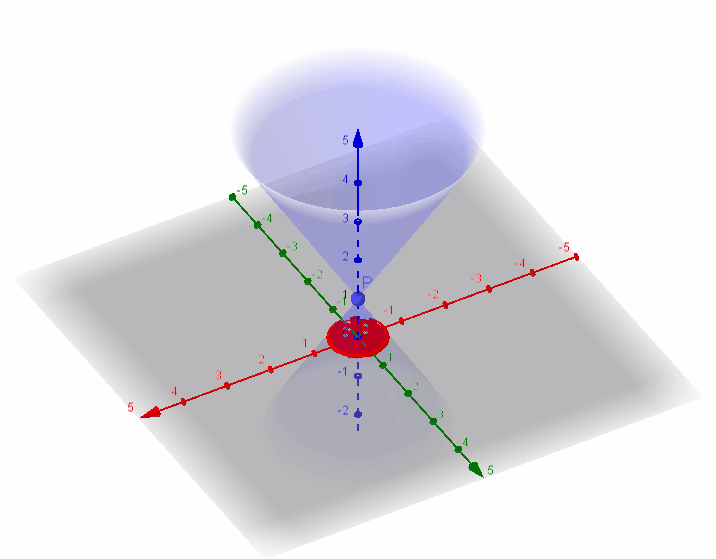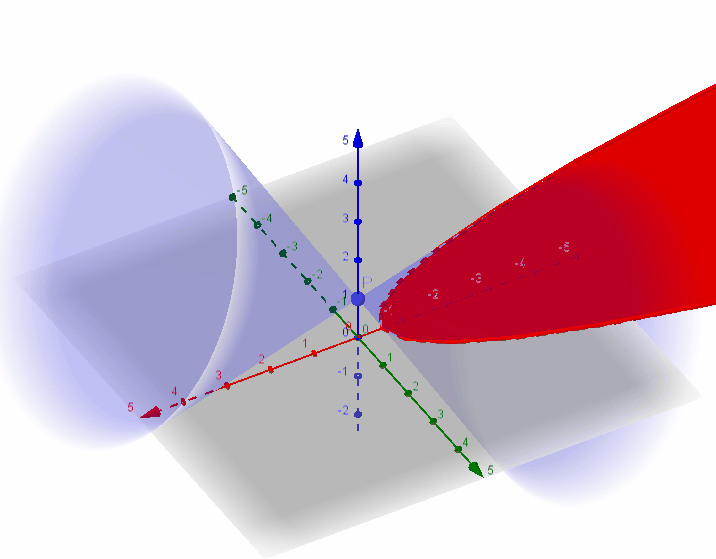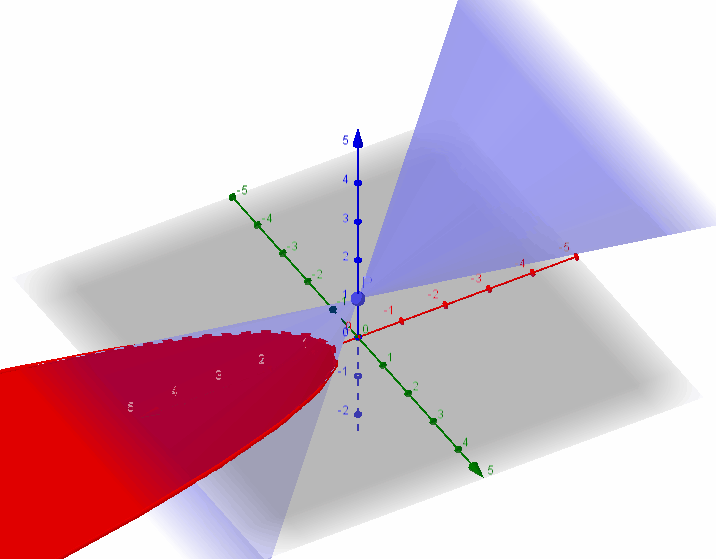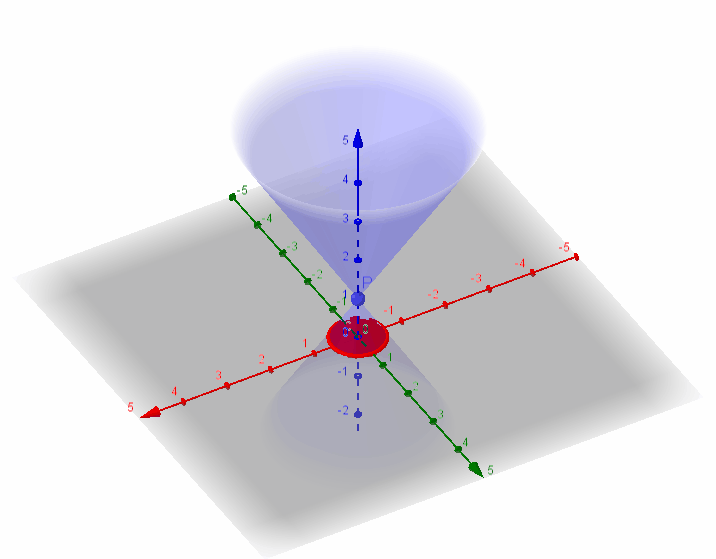
所截圆锥曲线是抛物线、椭圆还是双曲线可由离心率
二、第一定义
1、抛物线
由第五部分性质1知,当
圆锥的顶点设为
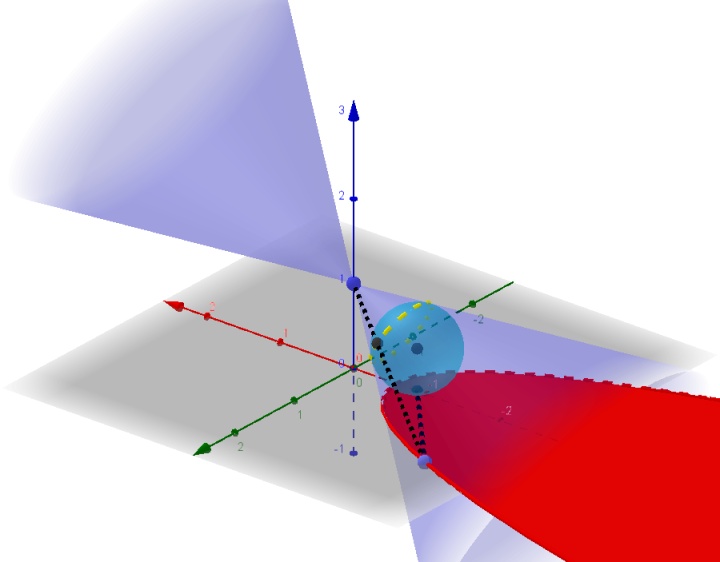
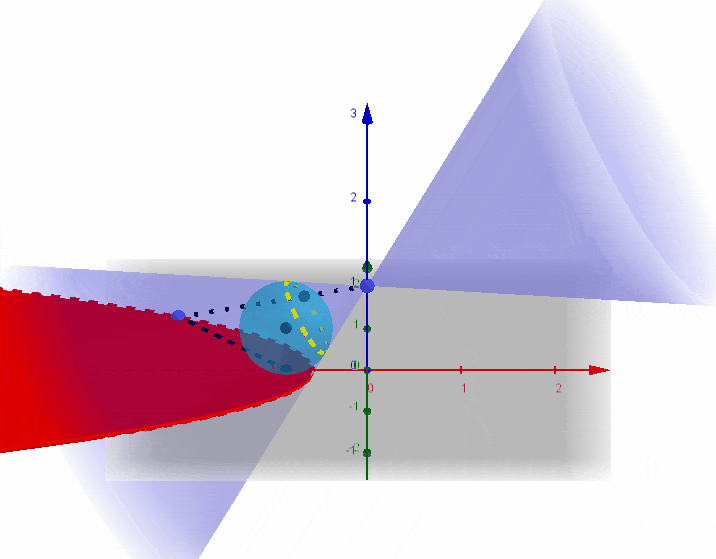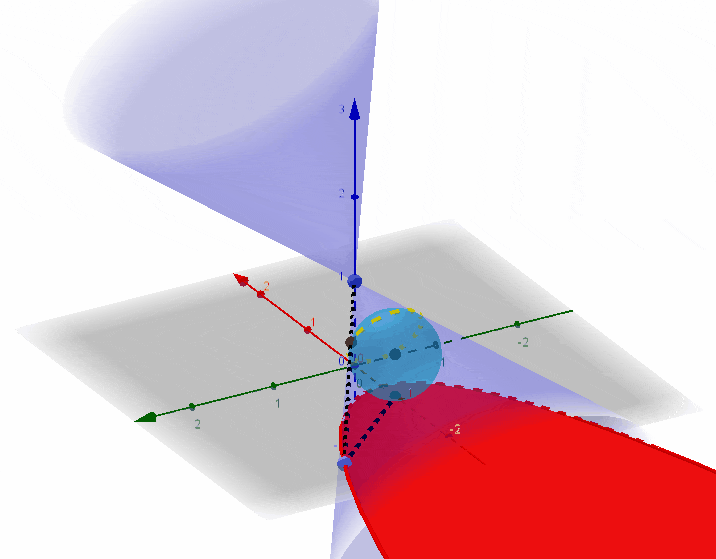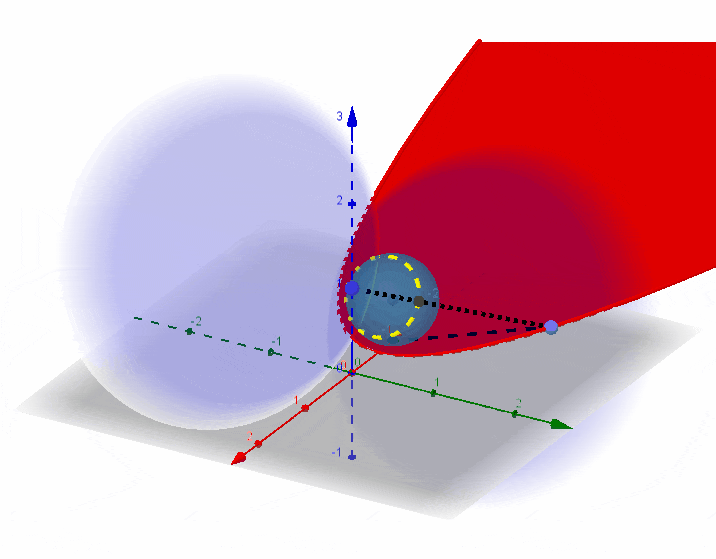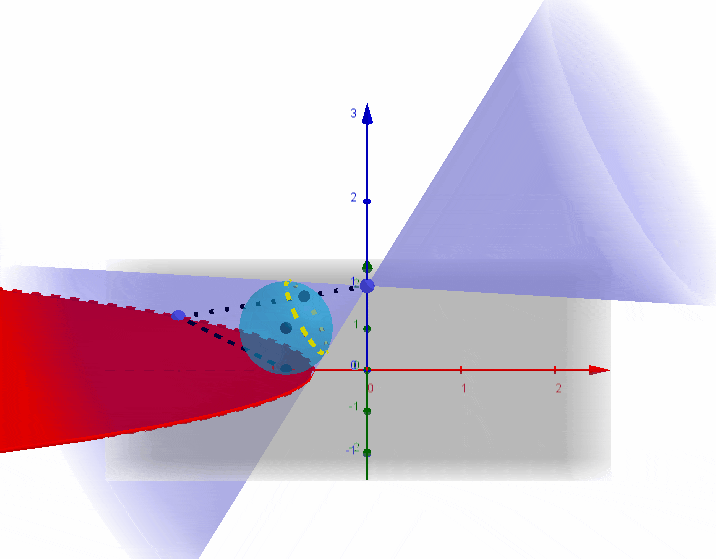
后续归于第三部分,统一证明。
2、椭圆
设圆锥顶点为
找到两个公切球,球心分别设为
在椭圆上任取一点


3、双曲线
设圆锥顶点为
找到两个公切球,球心分别设为
在双曲线上任取一点
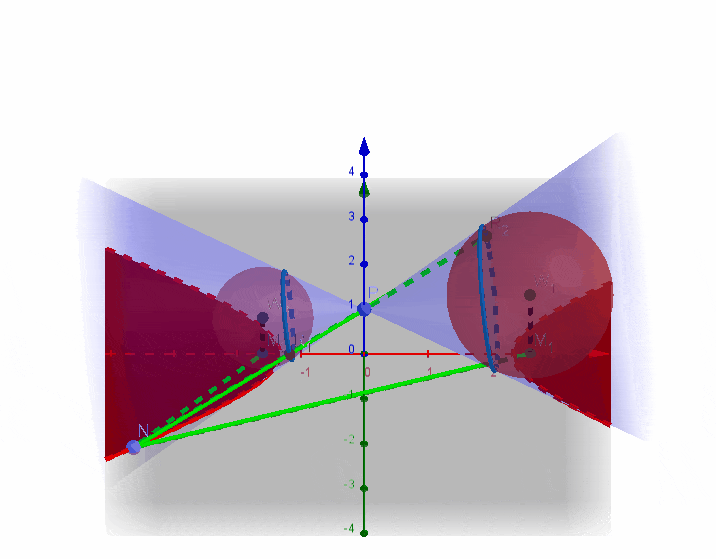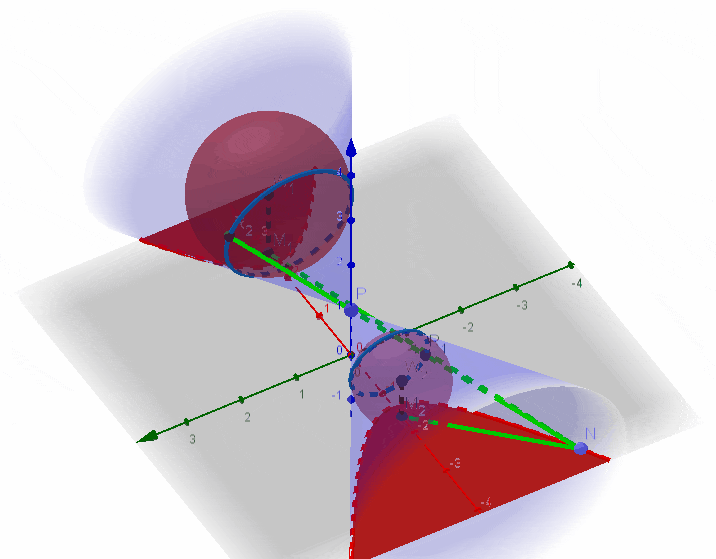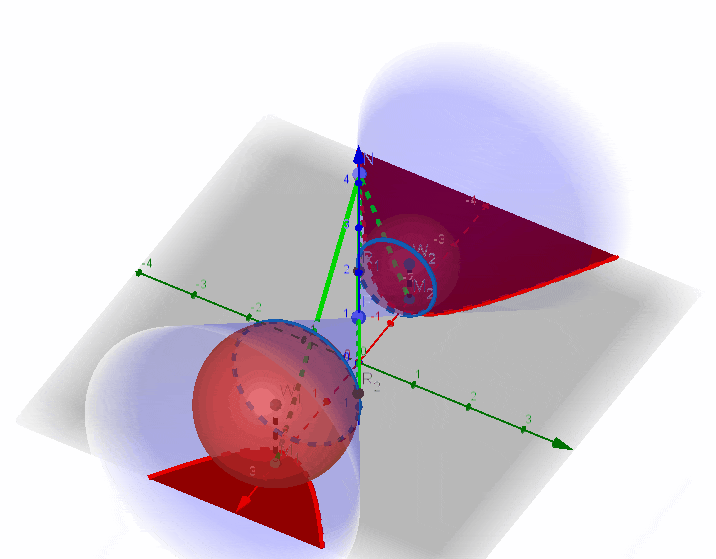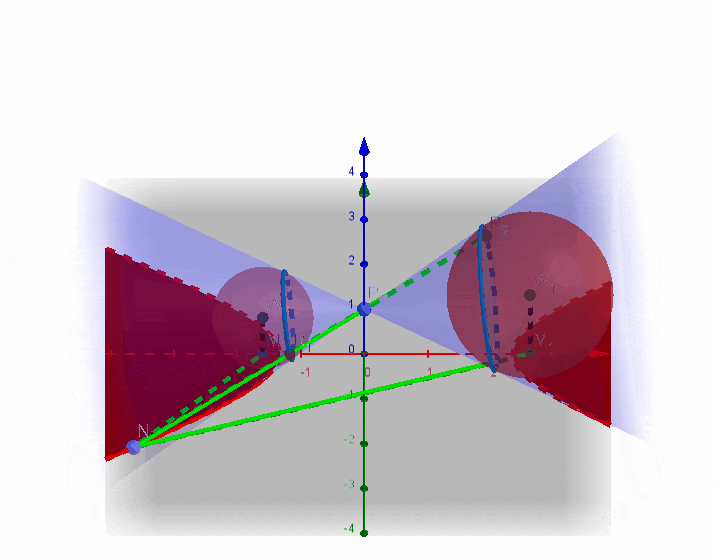
三、第二定义
这一部分的点很多,但是清楚其中的重要步骤就很好理解:
将有关边全部和圆锥轴线上的长度联系起来
以椭圆为例,设靠近原点的焦点为
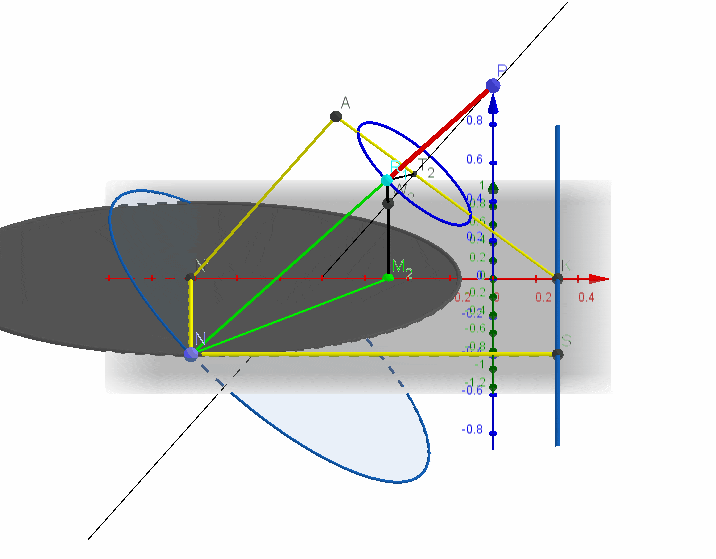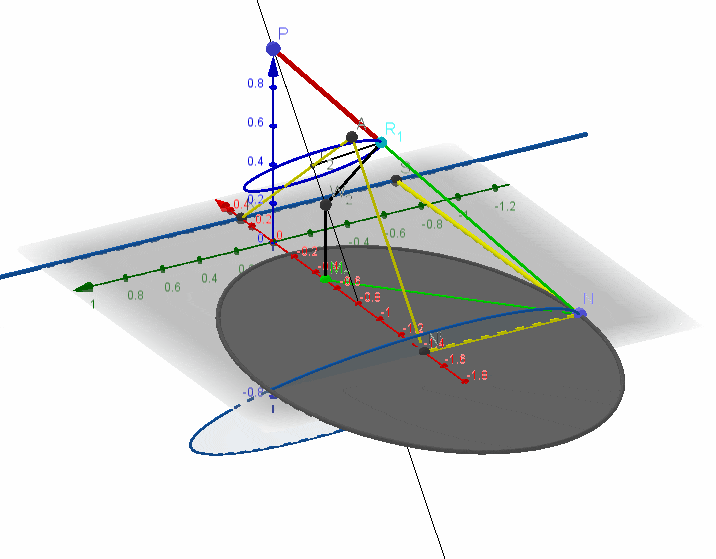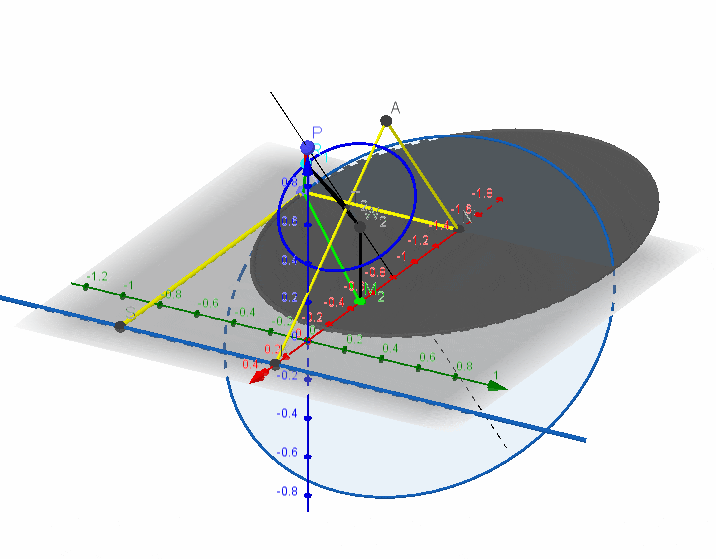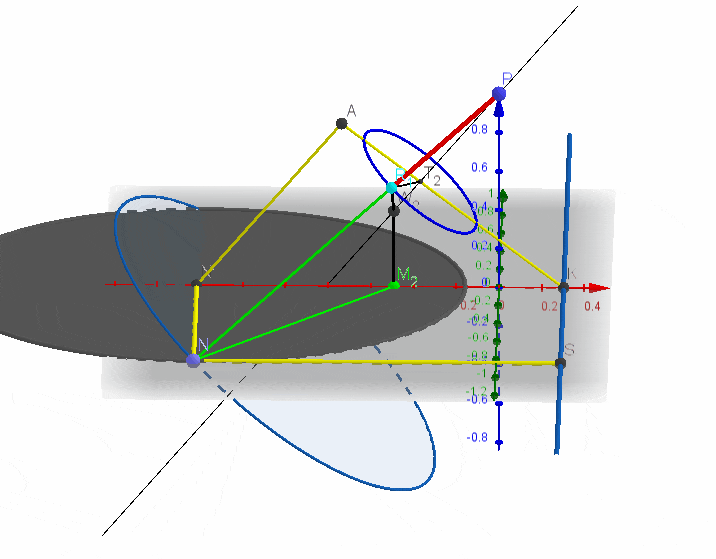
1、过
这样就得到了
2、其对应公切球为球
圆
这样四边形
又有
轴线与
3、由(3-1)以及(3-4),得
这就是圆锥曲线第二定义也就是统一定义得内容。
四、圆锥曲线的性质
性质1 由平面与圆锥所截得到的圆锥曲线的离心率
五、证明
1、圆锥曲线是二次曲线[2]
首先要知道圆锥的方程。
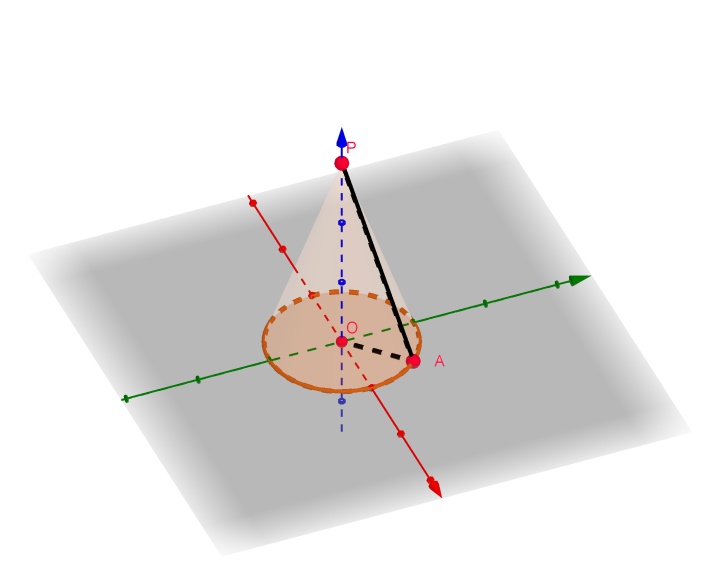
为定值,根据
即
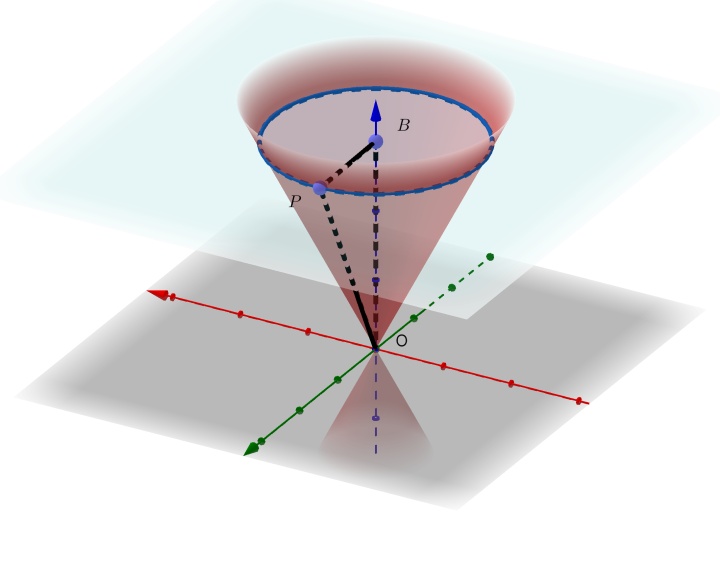
这就是以原点
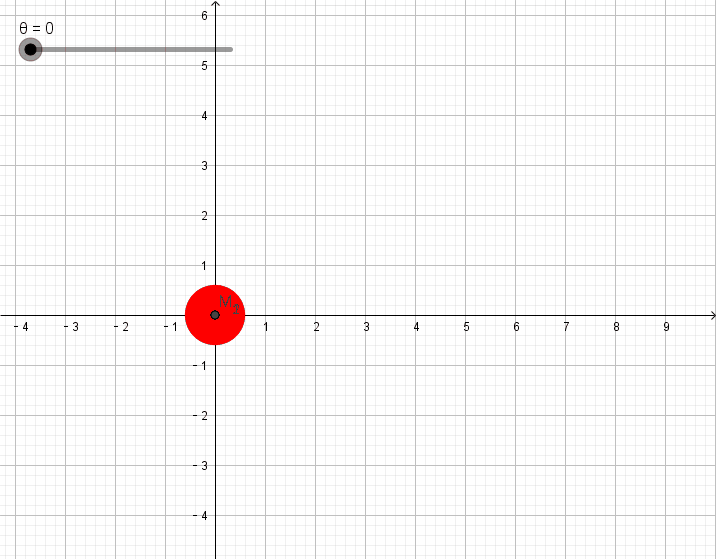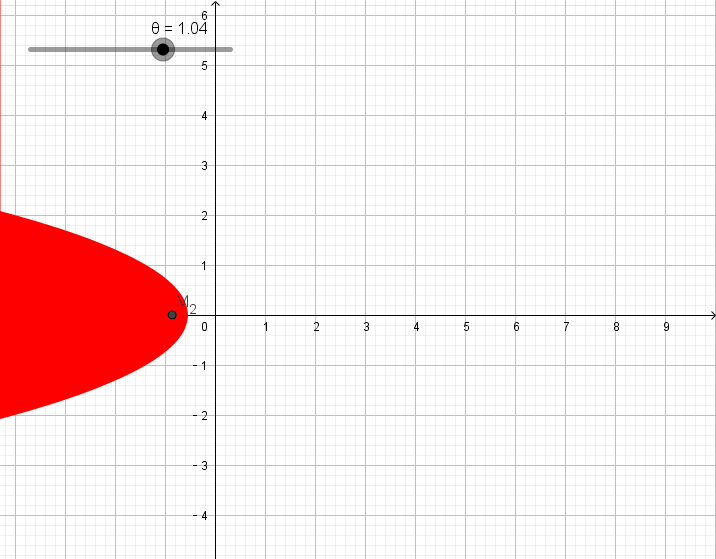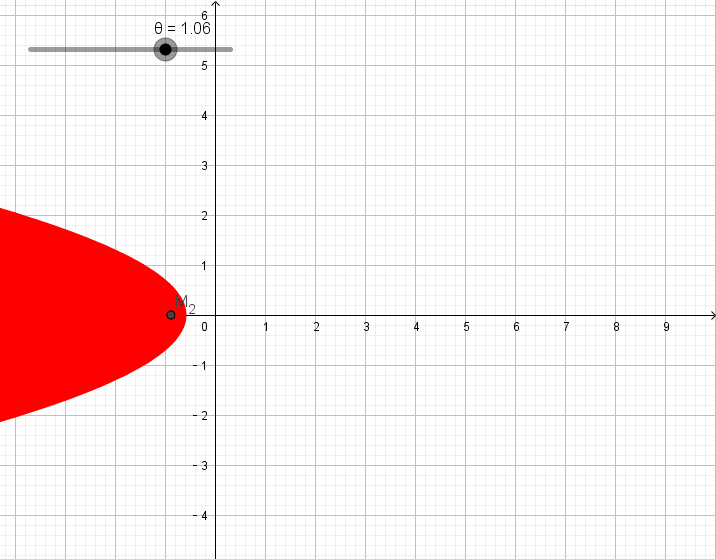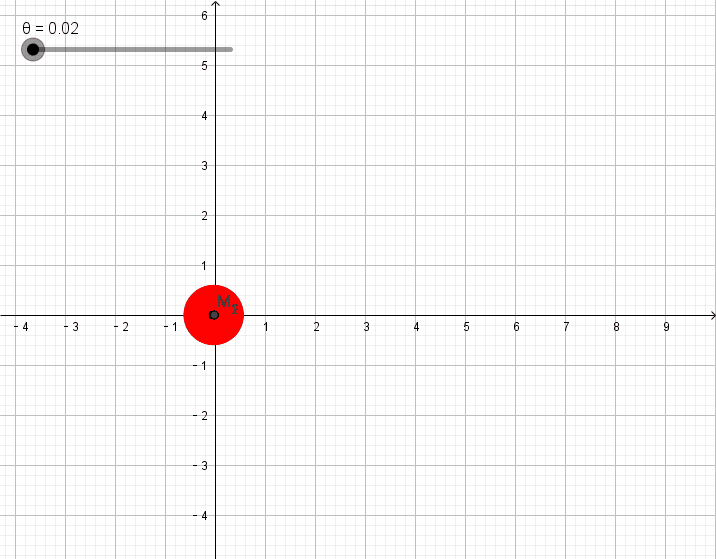
为了便于观看,我们选择固定平面,旋转圆锥截取圆锥曲线。
取截平面为
时为退化情况,圆锥与平面仅有以下三种情况:
(a) 仅有交点
(b)交线为一条直线,即 轴
(c)交线为相交于 的两条直线
图略圆锥方程为
圆锥绕
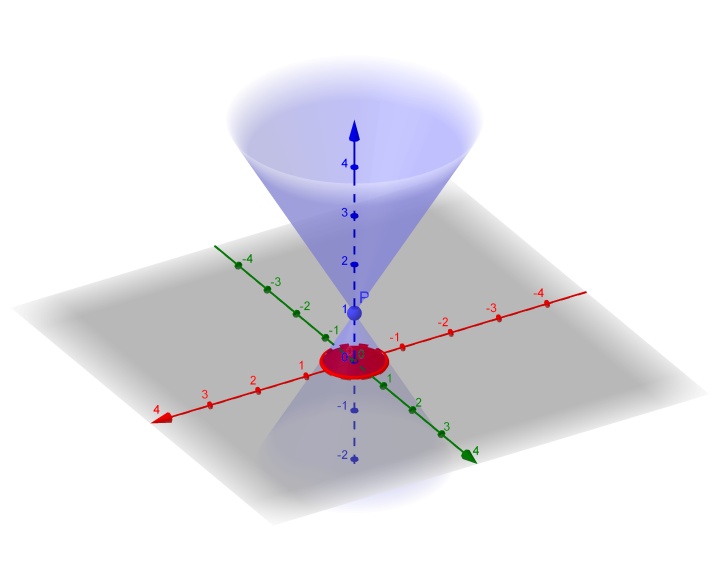
最后的旋转效果即为图2-1。
然后在
可以看出方程的最高次项是2次,说明这是二次曲线。
2、离心率分析[3]
化简
方程关于
(1)
得到圆,离心率
(2)
二次项系数均大于0,为椭圆,半焦距
这样算出离心率
(3)
得到抛物线,离心率
(4)
得到双曲线,半焦距
和
综上所述,我们可以得出结论:
圆锥曲线的离心率
3、寻找公切球
寻找公切球即要找到与截平面相切、在圆锥内部且与圆锥相切的球。
设球心
得
注意到其中
(a)当
球心坐标为
(b)当
得到这些数据后,我们就可画出(2-1)等图像。
4、计算准线位置
在寻找公切球的过程中,公切球的在
取焦点
要验证第二定义还要知道它的准线,根据定义式计算焦准距
所以准线方程为
这与三中利用平面截出的直线是相同的。
参考
- ^圆锥曲线百度百科 https://baike.baidu.com/item/%E5%9C%86%E9%94%A5%E6%9B%B2%E7%BA%BF/6691222?fr=aladdin
- ^二次曲线?圆锥曲线?画图试试 https://zhuanlan.zhihu.com/p/129034953
- ^离心率 https://zhuanlan.zhihu.com/p/129034953























 1270
1270

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








