3d模型多怎么优化_近似模型之响应面建模

近似模型方法是通过数学模型的方法逼近一组输入变量（独立变量）与输出变量（响应变量）的方法。

其中：是响应实际值，是响应近似值，为随机误差，服从标准正态分布。

基于近似模型进行优化设计的优势

• 建立经验公式，获得输入输出之间的量化关系；
• 减少耗时的仿真程序调用，提高优化效率（数量级的提升）；
• 对响应函数进行平滑处理，降低“数值噪音”，有利于更快的收敛到全局最优点。

表1近似建模算法

图1近似模型建模流程

响应面（RSM）模型

响应面方法是利用多项式函数拟合设计空间

优点：

• 通过较少的试验在局部范围内比较精确的逼近函数关系，并用简单的代数表达式展现出来
• 通过回归模型的选择，可以拟合复杂的响应关系，具有良好的鲁棒性
• 数学理论基础充分扎实，系统性、实用性强，适用广泛
• 缺点：
• 不能保证响应面通过所有的样本点，因此存在一定的误差
• 对于高度复杂的函数关系的逼近效果不如神经网络等方法

表2响应面阶数及样本需求

对于构造高阶响应面主要有一下两个问题：

• 样本量将显著增加，此外普通的试验设计也将更遭；
• 高阶响应面容易产生振动。

以一个简单的例子，简述响应面模型建模方法

A根据已有数据创建响应面模型

01 直接创建近似模型组件。

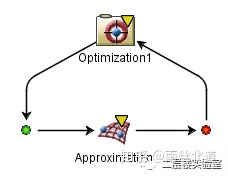
02 选择响应面模型。

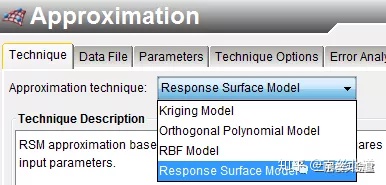
03 将原始数据[示例为.txt格式]导入。

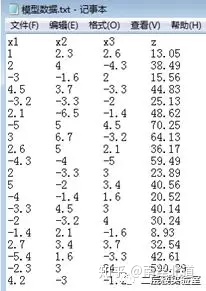
04 选择输入、输出数据。

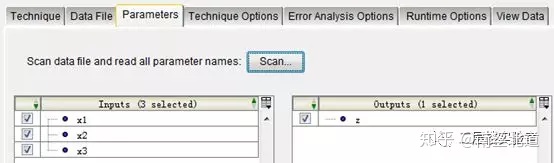
05 选择二阶响应面模型(若不知道模型阶次需尝试探索)，Sequential Replacement方法(代价较小)。

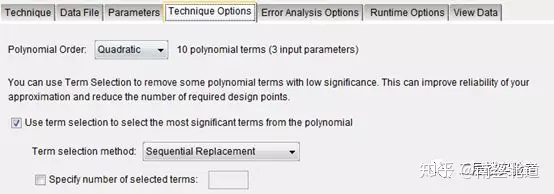
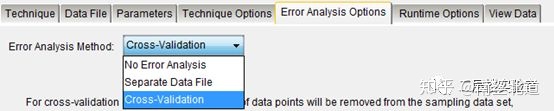
06 选择误差分析方法，独立数据(需额外独立的验证数据)或交叉验证。

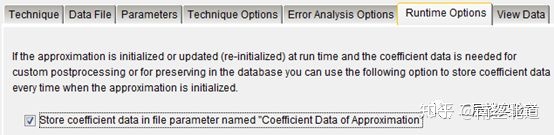
07 保留近似模型系数，方便后续分析。

08 初始化近似模型。

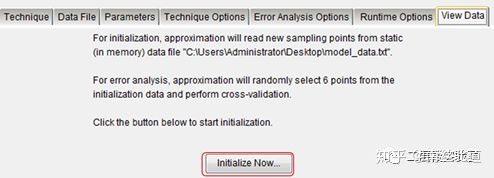
09 得到近似模型系数。近似模型为：

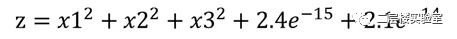
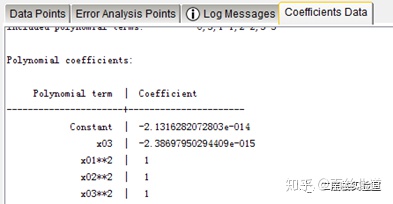
10 误差分析：

均方根误差：1.6E^-16

回归分析、残差分析、标准差分析等：

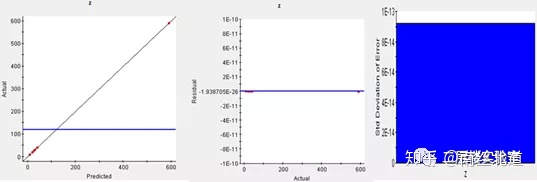
上述误差分析展现了响应面近似模型极高的精度。

而实际上，用以建模的原始数据是由：

生成。

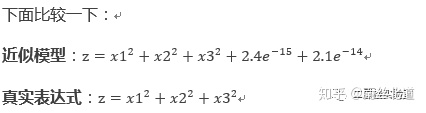
近似模型建好后，我们尝试求解z的最小值

直接选取NLPQLP算法

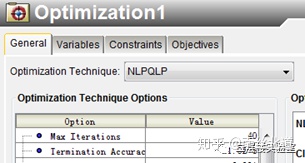
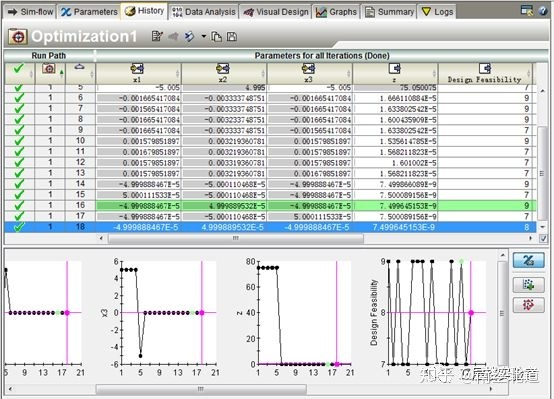
当然为阐述响应面模型建模方法，该例子所使用模型非常简单，实际工程问题远比本例复杂，对于样本数据和模型阶次的选择也需要多次探索研究，方能获得可靠的具有较高精度的响应面模型。此外，样本数据可由DOE抽样产生。

[阅读原文]

近似模型之响应面建模

- END -