数值积分与数值微分方法比较_矩阵与数值计算（17）——常微分方程的数值解法之基于数值积分的解法...

weixin_39830387

于 2021-01-29 20:46:03 发布

阅读量596

点赞数

文章标签：数值积分与数值微分方法比较

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/weixin_39830387/article/details/113536926

版权

本文介绍了数值积分在解决一阶常微分方程初值问题中的应用，包括线性单步法如Euler公式、隐Euler公式和梯形公式，并探讨了误差分析，如局部误差和整体误差。此外，文章还简要提及了两步法中的Simpson公式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

在科学与工程技术问题中，有很多问题的数学模型是常微分方程的初值问题或边值问题，研究这些问题的数值解法不仅有重要的理论意义，而且有广泛的实践意义。微分方程数值解法就是利用计算机求解微分方程近似解的数值方法。

一、一阶常微分方程的初值问题

对于形如

equation?tex=%5Cbegin%7Bcases%7D+u%27%3Df%28t%2Cu%29%2C%5Cquad+a%5Cle+t%5Cle+b%5C%5C+u%28a%29+%3D+u_0+%5Cend%7Bcases%7D

，这就是一阶常微分方程的初值问题。等价的积分方程为

equation?tex=u%28t%29+%3D+u_0%2B%5Cint_a%5Etf%28%5Ctau%2Cu%28%5Ctau%29%29d%5Ctau

，

若

equation?tex=f%28t%2Cu%29

满足Lipschitz条件，即存在常数L，对任意

equation?tex=t%5Cin%5Ba%2Cb%5D

，均有

equation?tex=%7Cf%28t%2Cu%29-f%28t%2C%5Cbar+u%29%7C%5Cle+L%7Cu-%5Cbar+u%7C

，则一阶常微分方程解存在且唯一。

但是对于这种问题大多数情况下不能求出解析解，因此只能通过数值解法求出数值解。

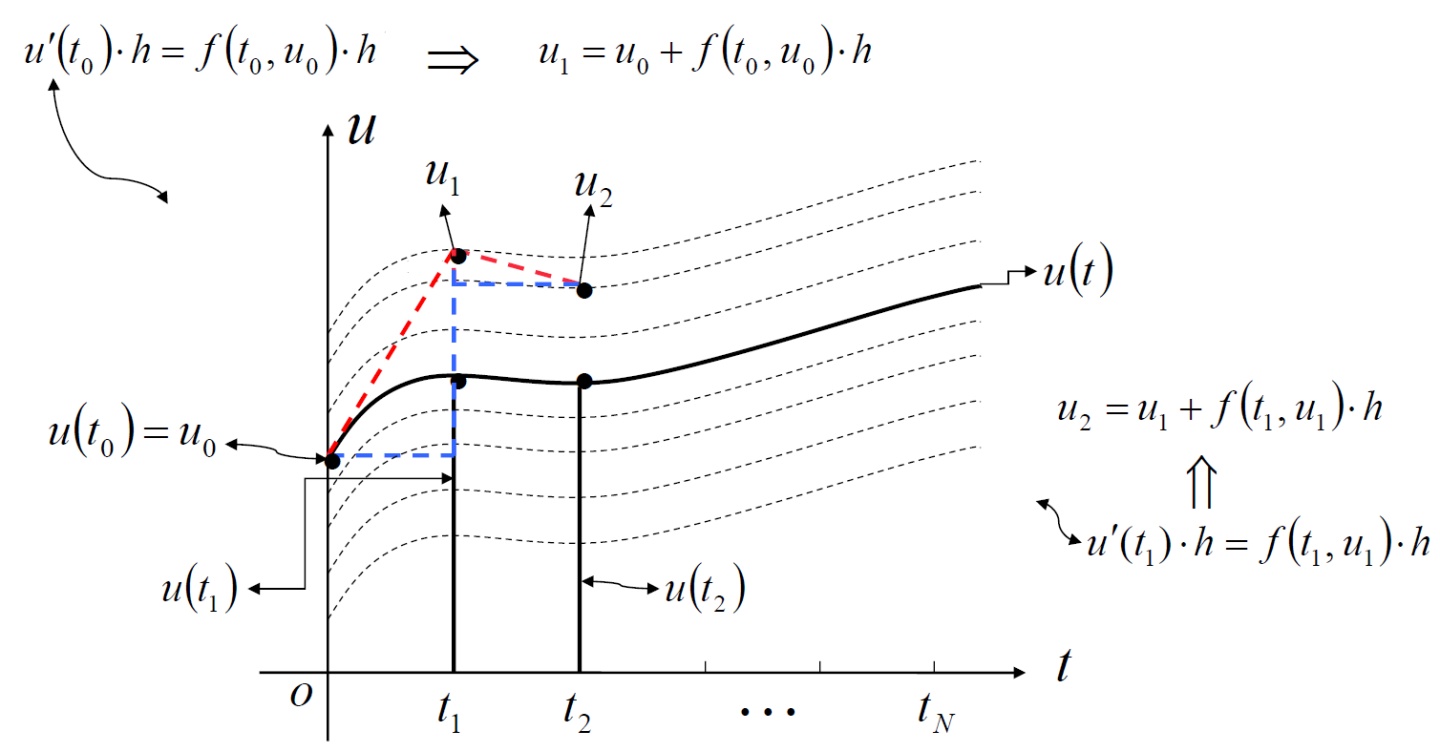
数值解法思想

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。