本文着重讨论循环神经网络(Recurrent Neural Network,RNN)的数学推导过程(主要是反向过程),不会对RNN做全面的介绍,其特点,缺点假定读者已经了解,并且假定读者已经掌握全连接(FC)神经网络的原理和相关函数的求导。当然,不清楚也没关系,下面的文章了解一下:
Numpy实现神经网络框架(1)
Numpy实现神经网络框架(2)——梯度下降、反向传播
Numpy实现神经网络框架(3)——线性层反向传播推导及实现
Softmax与交叉熵损失的实现及求导
本文后半部分更新了一种方法,使用更简单的结构来表示循环层,同时作为LSTM的铺垫
正文开始
为了使本文看起来更有条理性,并对相关符号进行说明,先从普通的神经网络开始,一个简单的全连接网络可以表示如下
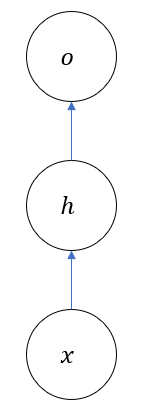
其中
其中
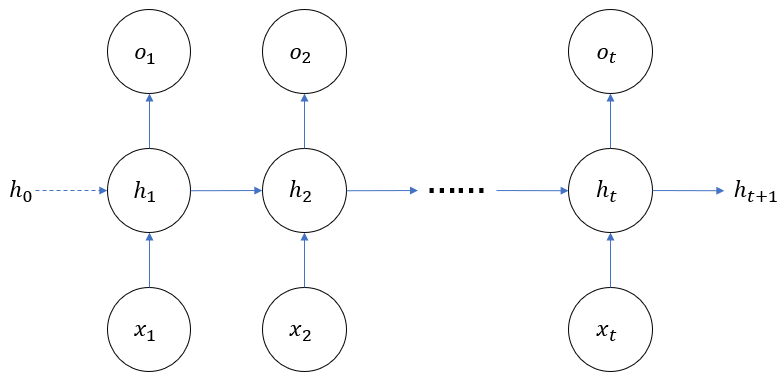
然后,再来看一个简单的RNN图示

上图相比全连接网络,就
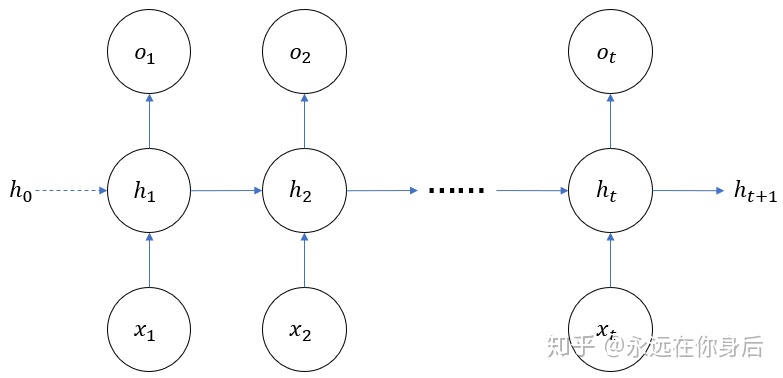
其中
可以看到,循环层不光取决于当前时刻的输入
相比全连接网络,主要变化在于
也就是上式中标红的部分,
上面的图示中,循环层只画了一个,实际中也可以使用多个,组成深度网络。不过即使有多个循环层,它们也是独立进行正、反向计算,所以只用一个循环层的例子弄清它的原理即可。接着是带上损失函数的图像

下面,我们从一个具体例子入手(包含三个时间序列),来推导RNN的反向过程
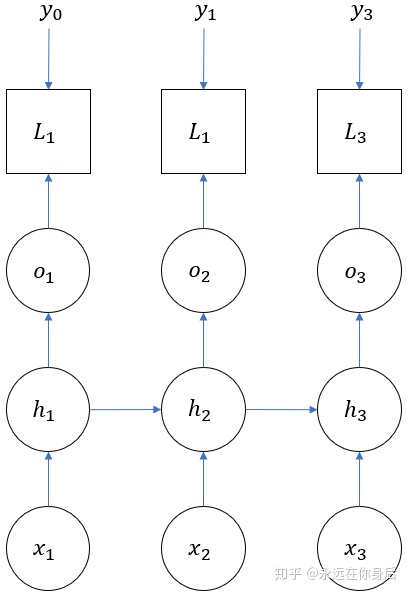
反向传播
首先,将正向计算的图拿过来,并且将其他节点都挖掉,只保留代表输入的节点,可以看作是RNN正向过程的一个框架,从箭头方向能够看正向过程的计算方向
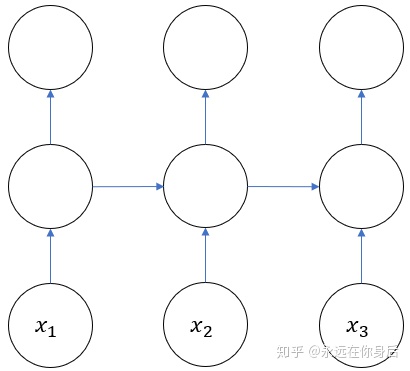
那么相应的,反向过程从直觉上来说,应该是按照与正向过程相反的方向进行计算,大致可以表示如下
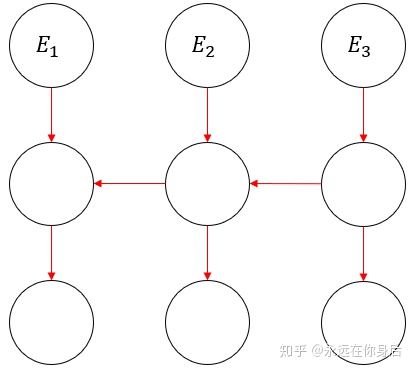
因为循环层是网络中唯一与之前的时刻有关联的,所以先把与之前时间序列无关的变量的梯度给求出来。为了具体的解释这句话的涵义,来看一张更详细的图
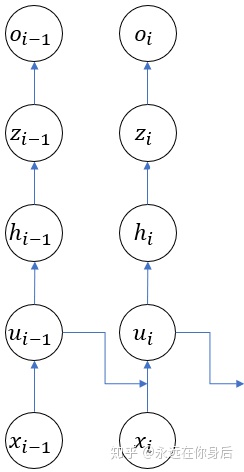
然后将
可以看到,真正参与计算
所以对于

首先来看输出
根据前面那篇softmax与交叉熵损失函数的文章可知,
然后是
可以得到当前时刻损失对于这两个参数的梯度
因为这两个参数每个时刻的梯度都是独立的,所以可以直接将所有时刻的梯度求和得到总梯度
然后是循环层激活函数
整理得到
其中
我们首先从正向计算的方向来推导,从最简单的
容易得到
所以
然后再来看
接着再计算
令
代入得到
所以
最后是
计算梯度
整理得到
以上是从正向计算入手,通过求导来得到参数的梯度,虽然也能看出规律,但是还是不如相反的方向计算更符合直觉。所以我们将上面上个式子调整一下
因为总梯度等于各个时刻梯度之和
所以将公式调整后总体梯度并不会改变。接着我们从调整后的公式入手,从反向推导得到相同的结论。首先从
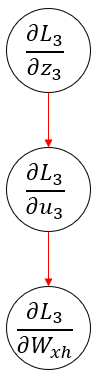
因为没有
再此基础上,我们考虑
图示如下
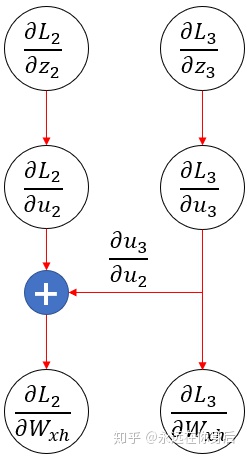
上图中蓝底十字表示将
接着,再将
图示如下

上图中将
另外前面的公式还是有点复杂,我们继续简化,再添加一个变量
各个时刻的
整体梯度
最终表示
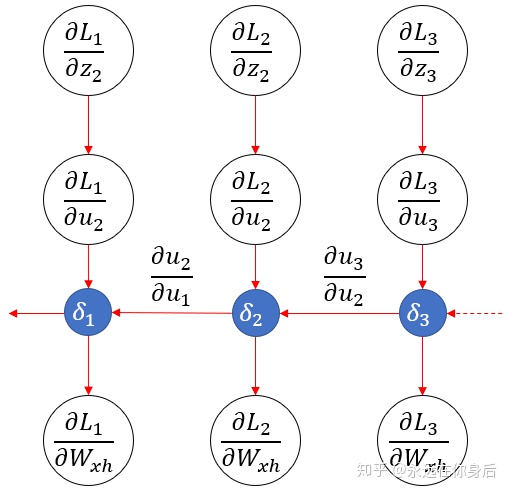
这样一来,和之前猜测的结构基本是一样的。这是一个符合直觉的结果,因为
以及
所有需要计算的梯度的公式已经推导出来了,最后简单实现一个循环层
class RecurrentLayer(object):
def __init__(self, shape):
'''
shape: (输出向量长度,输入向量长度)
'''
# 初始化正向计算的参数
self.h = 0
self.b = np.zeros(shape[0])
self.W_xh = np.random.randn(*shape)
self.W_hh = np.random.randn(shape[0], shape[0])
# 保存各个时刻的输入、激活值
self.h_list = []
self.x_list = []
# 初始化反向计算梯度
self.delta = 0 # 反向计算中的累积梯度
self.d_W_xh = 0 # 全部时刻损失对于 W_xh 的梯度
self.d_W_hh = 0 # 全部时刻损失对于 W_hh 的梯度
self.d_b = 0 # 全部时刻损失对于 b 的梯度
def tanh(self, x): # tanh激活函数
ex = np.exp(x)
esx = np.exp(-x)
return (ex - esx) / (ex + esx)
def forward(self, x):
'''
x: i时刻的输入
'''
# 保存前一时刻激活值 和 当前时刻输入
self.h_list.append(self.h)
self.x_list.append(x)
# 计算并返回当前时刻激活值
u = np.dot(self.W_xh, x) + np.dot(self.W_hh, self.h) + self.b
self.h = self.tanh(u)
return self.h
def backward(self, d_h):
'''
d_h: 反向计算中 i 刻损失 L_i 对 h_i 的梯度
'''
d_u = d_h * (1-np.square(self.h)) # 当前时刻损失 L_i 对 u_i 的梯度
self.delta = d_u + self.delta # 计算 u_i 的累积梯度
self.h = self.h_list.pop() # 弹出 i-1时刻的激活值
# 根据 u_i 的累积梯度,计算参数的梯度并累加
self.d_W_xh = self.d_W_xh + np.dot(self.delta, self.x_list.pop().T)
self.d_W_hh = self.d_W_hh + np.dot(self.delta, self.h.T)
self.d_b = self.d_b + self.delta
res = np.dot(self.W_xh.T, self.delta) # x_i 的梯度,往回传
tmp = self.W_hh.T * (1-np.square(self.h)) # u_i 对于 u_{i-1} 的梯度
self.delta = np.dot(tmp, self.delta) # 更新累积梯度,以便 i-1 时刻反向计算时使用
return res更新部分
以下部分的内容作为下一篇关于LSTM(long short term memory,长短时记忆网络)的铺垫,不会涉及LSTM的内容,只是将循环层的结构进行简化——整体功能当然是和原来一样——以便帮助理解下一篇的LSTM
先说结果,结构变化后的循环层内部包含一个线性层。其实就是将循环层模块化,把它本身视作一个小型网络,不过只从输入输出的角度来看的话,它是没有区别的:
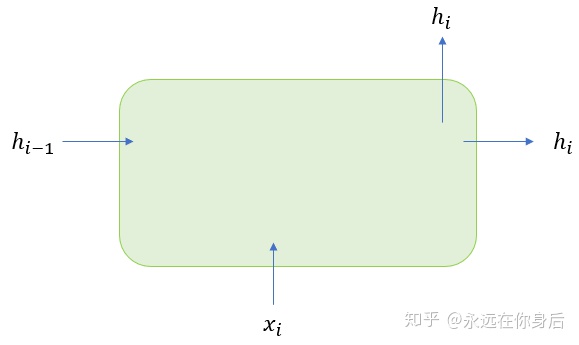
上图表示正向过程的输入输出,水平方向的
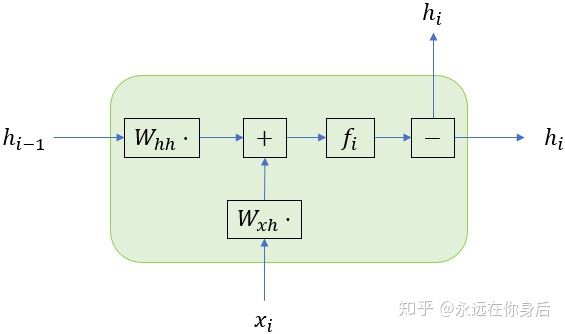
其中每一个黑色边框的矩形表示某种操作,或者说进行某些计算,例如
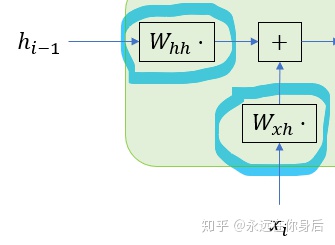
上图中蓝圈中标记的部分本别表示
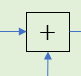
表示将两个箭头来源表示的变量进行相加,再加上阈值(如果有的话),其实就是对应着我们之前的式子:
然后是
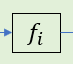
自然表示
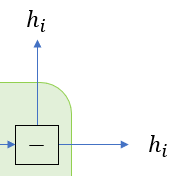
减号并不是减去什么,而是一个分流的表示,只是将输入的变量向两个(或多个)方向传递。之所以这么额外弄这么一个方块,因为在反向过程中,这里的减号变成了加号,表示将这两个方向的梯度进行相加。自然的,正向过程中的加号在反向过程中也变成了减号,如下图所示
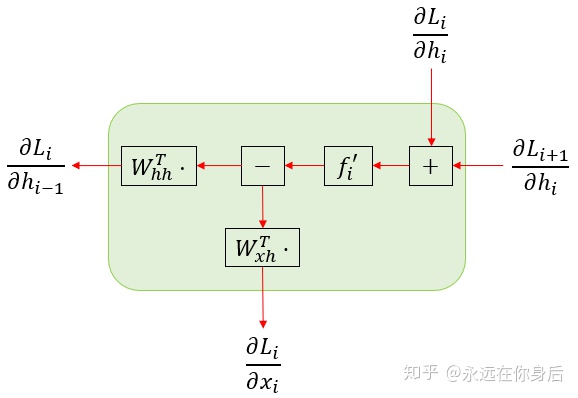
这里说明一下:
为了验证上图所表示的计算结果与之前一样,首先将前面的一些变量拿来回顾一下,方便后面讨论
首先,从最后一个时刻
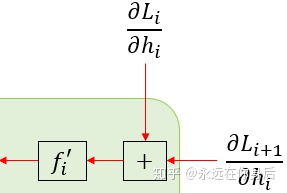
上图两个矩形表示的计算的结果为:
然后将
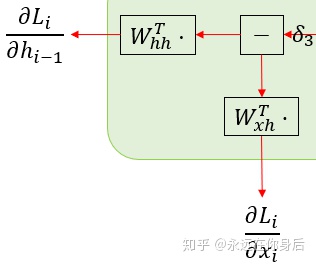
按照图示,我们可以得到
关于
将
得到了
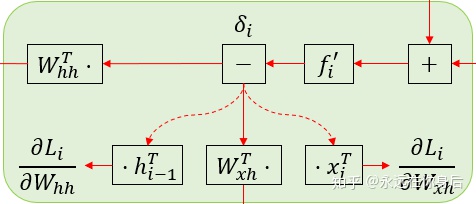
根据图示,我们也可以轻松得到参数的梯度
这样一来,得到了和我们之前计算的一样的结果,但是如果只是这样的话是没必要的,需要进一步简化,即将其内部的部分“组件”打包成一个独立的线性层来简化复杂度
首先,来观察
其中红色部分可以写成矩阵乘法的形式
然后我们令
所以
可以用下图表示
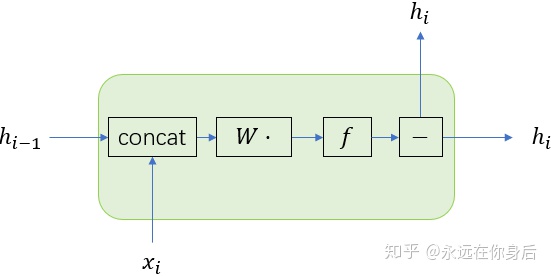
其中concat的矩形其作用不言自明,然后是下图
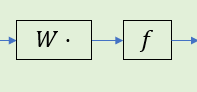
这两部分加起来不就是一个带激活函数的线性层吗?
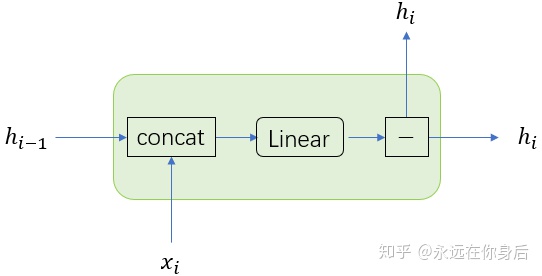
正向过程就不推导了,直接来看反向过程
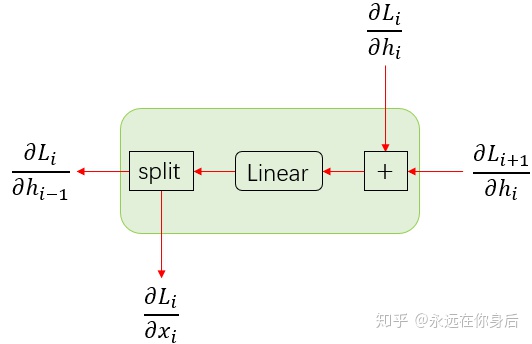
再来验证一下线性层反向过程的计算,对于线性层来说,其反向过程的输入为加号部分的输出,即:
当这两个梯度之后传入线性层的反向函数后,首先是乘上激活函数的导数,得到
接着我们就可以计算梯度了
以及
然后是线性层反向函数的输出
可以看到,计算得到的结果和原来是一样的,所以内部包含的线性层是可以独立实现的:
class Linear(object):
def __init__(self, shape):
'''
shape: 权重矩阵的shape,由循环层构造
'''
self.W = np.random.randn(*shape)
self.b = np.zeros(shape[0])
# 保存输入输出的列表
self.input_list = []
self.output_list = []
# 全部时刻损失对参数的梯度
self.d_W = 0
self.d_b = 0
def tanh(self, x): # tanh激活函数
ex = np.exp(x)
esx = np.exp(-x)
return (ex - esx) / (ex + esx)
def forward(self, x):
'''
x: 由循环层拼接 x_i 和 h_{i-1} 而成的列向量
'''
output = self.tanh(np.dot(self.W, x) + self.b)
# 保存正向计算的输入输出
self.input_list.append(x)
self.output_list.append(output)
return output
def backward(self, d_h):
'''
d_h: 当前时刻损失 L_i 及之后时刻损失对 h_i 的梯度之和
'''
input_ = self.input_list.pop()
output = self.output_list.pop()
delta = d_h * (1 - np.square(output))
# 计算当前时刻参数的梯度并累加
self.d_b = self.d_b + delta
self.d_W = self.d_W + np.dot(delta, input_.T)
return np.dot(self.W.T, delta) # 传递梯度给循环层基本上和普通的线性层是一样的,只不过多了两个列表保存各个时刻的输入输出用来进行反向过程的计算
然后是循环层,代码就简单多了
class Recurrent(object):
def __init__(self, shape):
'''
shape: (输出向量长度,输入向量长度)
'''
linear_shape = (shape[0], shape[0]+shape[1])
self.linear = Linear(linear_shape)
self.h = np.zeros((shape[0],1)) # 不能再直接初始化为0
self.d_h_ = 0 # 反向计算时,L_{i+1} 对 h_i 的梯度
def forward(self, x):
s = np.vstack(x, self.h) # 拼接 x_i 及 h_{i-1}
self.h = self.linear.forward(s) # 更新 h_i
return self.h
def backward(self, d_h):
d_s = self.linear.backward(d_h + self.d_h_)
self.d_h_ = d_s[-len(d_h):] # 分割线性层的输出,更新 L_{i} 对 h_{i-1} 的梯度
return d_s[:-len(d_h)] # 返回 L_{i} 对 x_i 的梯度由此,我们通过将循环层内部的一些计算过程打包为一个独立的线性层,从而降低了复杂度,以便我们更好的理解




















 694
694











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








