n平方的求和公式_极限求解--数列前n项和公式推导（补充知识）

0 序言

在求和型数列中，常用的方法是夹逼准则结合定积分知识，这部分内容我会在下一次笔记中更新，本篇主要是介绍一下对于一些特定求和型的数列，我们常见的求和公式以及对这些公式进行不同方法的推导，当作是课外知识的补充。

1 常见求和公式

【记忆】

其中，（3）有一个口诀是“前N个自然数的立方和等于其和的平方”；

（4）和（5）实际上是同一类，即等于最后一个项再往后乘一个数，然后除以项的个数，如（4）最后一项是

，再往后一项就是

，项的个数就是3，就可以记住

了。看下面的推导方法1就可以深刻记住了！

2 公式推导

在这里，我们是要在不知道求和后的公式情况下进行推导记忆，所以不会选择数学归纳法法。 本篇利用的方法主要由两种类型，一种是带有一定技巧性但可以普遍使用的组合公式法，一种是不管三七二十一的暴力待定系数法。

【组合公式法】

这里的核心公式是

，下面简单推导一下：

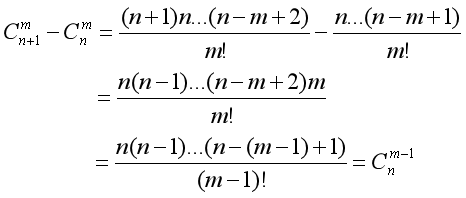
主要针对公式（4）进行推导，因为（4）和（5）的推导思路是一样的，由（4）和（5）通过公式的转化也不难得到（2）和（3）。

下面来推导公式（4）：

首先由上面的组合基本等式，可得

=

=

=

原式=

=

=

同样的思路可以推得（5）以及继续增加项的式子和。

【待定系数法】

这种方法就比较简单暴力了，记住一个规律，就是“通项为g个数相乘的数列求和，和的最高次幂不超过(g+1)”。

举个例子，我们可以看到，在式子（4）中，通项是

，即为2个数相乘，那么它的数列和的最高次幂不超过3，这里也就是n的3次方。

有了这个思路，那我们相求它的和就不管它什么形式了，直接利用待定系数就完事了。

还是用（4）做例子进行推导：

设

我们可以将n引申到n=0，直接可得d=0，这也是为什么所有公式都带有n以及没有常数项。

即

将

代进去，可得

即

=