均值和期望一样吗_理解期望、方差常见公式

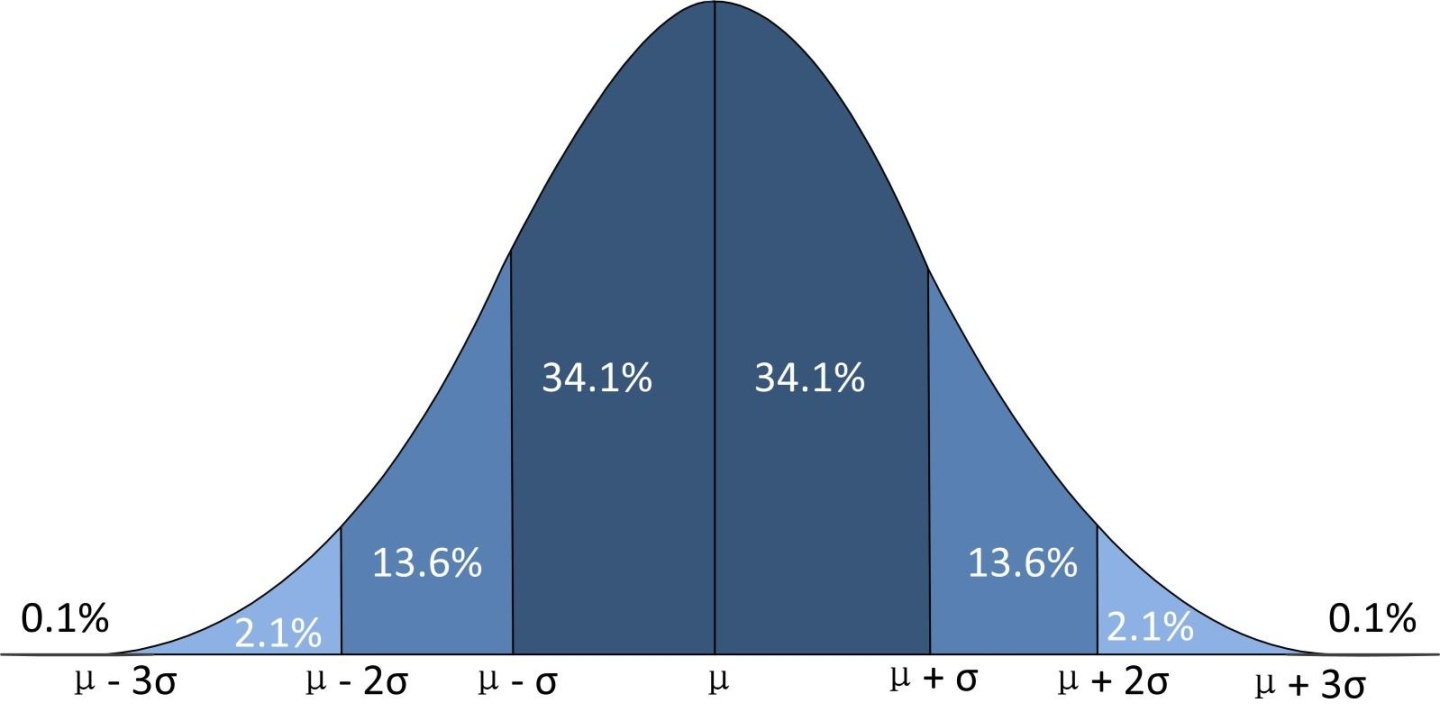
先从基本概念讲起。

期望

对于一个随机变量

，它在取不同值时的概率用函数

表示。比如色子的点数是一个随机变量，它为1的概率可以表达成

，这与我们代数中的函数有点不同，代数中的函数是输入一个确切的数，而这里不是。我甚至可以用

来表示投硬币为正面的概率。不过，本文其余部分都要求概率函数的输入值是数字。 期望表示随机变量的中心位置。例如你投色子很多次，最后计算的点数平均值应该是所有点数的均值，因为出现每种点数的概率相同。如果概率不同，则需要用概率加权，于是我们的期望公式就是：

它表示把每一种可能的输出的值乘以其概率后求和。

性质1: 期望的线性关系

对于两个相互独立的随机变量

，我们有：

这个就不做证明了，举一个直观例子说明：有2个色子各自投掷，两者的期望都是

，那么问两个色子之和的期望，显然是

。这是可以直观认知的。用

表示一个常数，它只是缩放每一个随机变量的值而已，进一步推广我们有：

性质2: 样本均值的期望

假定有一个随机变量

的期望值和方差分别是

。现在对这个数据集进行随机抽样（有放回的抽样，因为我需要保证整体的分布是不变的），抽到的样本一个一个的数据用

表示，现在试求

的期望。 根据样本均值的定义我们有：

根据性质1的推论：

。由于每个

所属的分布和

是一样的。两者都是有放回地随机抽一个，因此：

我们的结论是：有放回的随机抽样的样本均值和总体均值的期望是一致的。

性质3: 期望的乘积关系

对于两个相互独立的随机变量

，我们有：

这里给一个比较容易理解的说明，而不是证明： 首先，令

，

。于是有：

仔细观察可以发现，根据乘法结合律我们得到了

与

之间的所有组合，如

等。 由于是两个独立随机变量，因此两者之积的概率满足

。我们得到了两者乘积的每一个可能值，以及它们对应的概率，全部加起来就是期望的定义。

方差

方差用于表示数据的分散程度。数据波动越大，方差就越大。定义如下：

性质1

如果随机变量

变成

会如何（

为常数）？显然它只是最后输出的值改变了倍数，但是每个输出的值的概率是一样的，即

。但是，均值会放大

倍。于是根据方差定义得：

性质2

如果随机变量

变成

呢？其实也就是减去一个常数（总体的期望）再平方。想象色子的点数分别减3.5再平方，变成

，然而每个新的点数出现的概率还是不变，所以

。如果我们求这个新变量的期望：

没错，这正是方差的公式。这个式子可以认为是方差的第二种定义，它和第一种定义是等价的。 令

，再重复一遍公式：

性质3

证明之前的准备：

1.

视为一个常数：

2. 概率之和恒为1：

证明： 根据方差的性质2以及期望的一些性质有：

这个可以视为方差的第三个定义式。记忆口诀：“期望平方内减外”。

性质4

如果

是独立的随机变量，那么

。

证明： 根据方差的性质3和期望的性质3有：

推广得：如果

是一组独立的随机变量，则

。证明和上面基本类似，略。

性质5: 样本均值的方差

假定有一个随机变量

的期望值和方差分别是

。现在对这个数据集进行随机抽样（有放回的抽样，因为我需要保证整体的分布是不变的），抽到的样本一个一个的数据用

表示，现在试求

的方差。 根据样本均值的定义我们有：

根据方差的性质1和性质4有：

由于单个的

和

是等价的，因为属于同一分布，因此有：

也就是说，样本均值的方差是小于总体的方差的，并且会随着抽样次数增大而减小。这也是符合直觉的，因为你抽了一组样本求平均，当然就会减少数据的波动性。

标准差和标准误差

标准差 standard deviation 和 standard error 标准误差，两者都是用来表示数据的变异性，不同之处是前者是通过总体计算，后者是通过样本计算。所谓标准差就是总体的方差的算术平方根，记为

。 而一个容量为

的样本的是标准差，叫做标准误差，其值为

。（直接对方差的性质5的式子开方即得 ）

参考资料

https://newonlinecourses.science.psu.edu/stat414/node/167/ (貌似已失效)