python非线性规划求解_python中线性规划中的单纯形法、scipy库与非线性规划求解问题...

python中线性规划中的单纯形法、scipy库与非线性规划求解问题,线性规划,变量,在这里,插入图片,最优

python中线性规划中的单纯形法、scipy库与非线性规划求解问题

单纯形法、scipy库与非线性规划求解问题单纯形法的基本定义大M法求解线性规划的原理excel求解Python调用optimize包和scipy求解线性规划Python编程实现单纯形法对比情况非线性规划

单纯形法的基本定义

单纯形法的基本定义：

一般线性规划问题中当线性方程组的变量数大于方程个数，这时会有不定数量的解，而单纯形法是求解线性规划问题的通用方法。 具体步骤是，从线性方程组找出一个个的单纯形，每一个单纯形可以求得一组解，然后再判断该解使目标函数值是增大还是变小了，决定下一步选择的单纯形。通过优化迭代，直到目标函数实现最大或最小值。 换而言之，单纯形法就是秉承“保证每一次迭代比前一次更优”的基本思想：先找出一个基本可行解，对它进行鉴别，看是否是最优解；若不是，则按照一定法则转换到另一改进后更优的基本可行解，再鉴别；若仍不是，则再转换，按此重复进行。因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。如果问题无最优解，也可用此法判别。

大M法求解线性规划的原理

大M法求解线性规划的原理：

大M法首先将线性规划问题化为标准型。如果约束方程组中包含有一个单位矩阵I，那么已经得到了一个初始可行基。否则在约束方程组的左边加上若千个非负的人工变量，使人工变量对应的系数列向量与其它变量的系数列向量共同构成-一个单位矩阵。以单位矩阵为初始基，即可求得一-个初始的基本可行解。 为了求得原问题的初始基本可行解，必须尽快通过迭代过程把人工变量从基变量中替换出来成为非基变量。为此可以在目标函数中赋予人工变量一个绝对值很大的负系数-M。这样只要基变量中还存在人工变量，目标函数就不可能实现极大化。 以后的计算与单纯形表解法相同，M只需认定是一个很大的正数即可。假如在单纯形最优表的基变量中还包含人工变量，则说明原问题无可行解。否则最优解中剔除人工变量的剩余部分即为原问题的初始基本可行解。

excel求解

题目：

利用包求解：

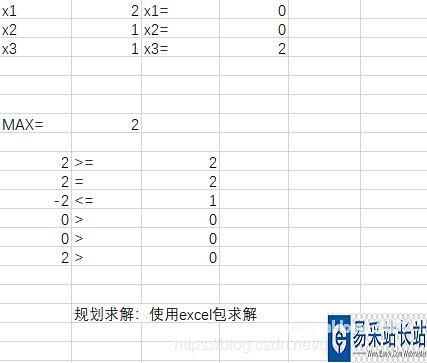
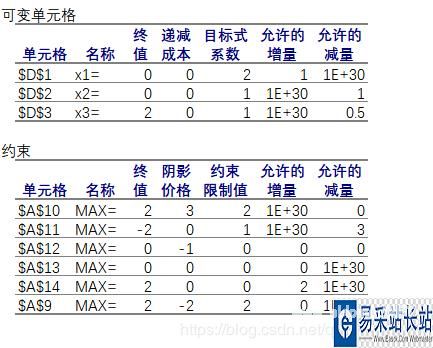
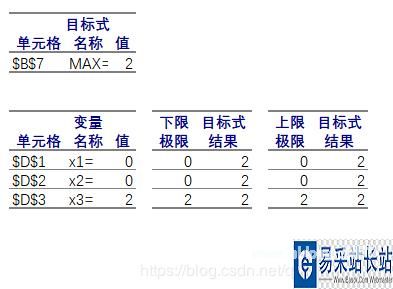
Excel使用大M法求解线性规划：

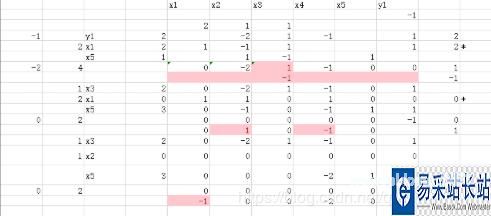
Python调用optimize包和scipy求解线性规划#导入包

from scipy import optimize

import numpy as np

#确定c,A_ub,B_ub

c = np.array([50,100])

A_ub = np.array([[1,1],[2,1],[0,1]])

B_ub = np.array([300,400,250])

#求解

res =optimize.linprog(-c,A_ub,B_ub)

print(res)

结果：

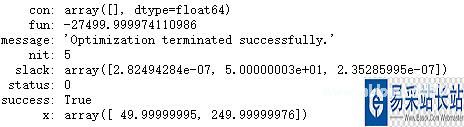
Python编程实现单纯形法import numpy as np

def pivot(d,bn):

l = list(d[0][:-2])

jnum = l.index(max(l)) #转入编号

m = [] for i in range(bn):

if d[i][jnum] == 0:

m.append(0.)

else:

m.append(d[i][-1]/d[i][jnum])

inum = m.index(min([x for x in m[1:] if x!=0])) #转出下标

s[inum-1] = jnum

r = d[inum][jnum] d[inum] /= r

for i in [x for x in range(bn) if x !=inum]:

r = d[i][jnum] d[i] -= r * d[inum]def solve(d,bn):

flag = True

while flag:

if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0

flag = False

else:

pivot(d,bn)

def printSol(d,cn):

for i in range(cn - 1):

if i in s:

print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])

else:

print("x"+str(i)+"=0.00")

print("objective is %.2f"%(-d[0][-1]))

d = np.loadtxt("./data.txt", dtype=np.float)

(bn,cn) = d.shape

s = list(range(cn-bn,cn-1)) #基变量列表

solve(d,bn)

printSol(d,cn)

data数据：

结果：

对比情况

两种结果对比,就值而言，两种方式基本一样误差不大，但单纯形法的结果更加精确为整数值。

非线性规划# coding=utf-8

from scipy.optimize import minimize

import numpy as np

# demo 2

#计算 (2+x1)/(1+x2) - 3*x1+4*x3 的最小值 x1,x2,x3的范围都在0.1到0.9 之间

def fun(args):

a,b,c,d=args

v=lambda x: (a+x[0])/(b+x[1]) -c*x[0]+d*x[2] return v

def con(args):

# 约束条件 分为eq 和ineq

#eq表示 函数结果等于0 ； ineq 表示 表达式大于等于0

x1min, x1max, x2min, x2max,x3min,x3max = args

cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\

{'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\

{'type': 'ineq', 'fun': lambda x: x[1] - x2min},\

{'type': 'ineq', 'fun': lambda x: -x[1] + x2max},\

{'type': 'ineq', 'fun': lambda x: x[2] - x3min},\

{'type': 'ineq', 'fun': lambda x: -x[2] + x3max})

return cons

if __name__ == "__main__":

#定义常量值

args = (2,1,3,4) #a,b,c,d

#设置参数范围/约束条件

args1 = (0.1,0.9,0.1, 0.9,0.1,0.9) #x1min, x1max, x2min, x2max

cons = con(args1)

#设置初始猜测值

x0 = np.asarray((0.5,0.5,0.5))

res = minimize(fun(args), x0, method='SLSQP',constraints=cons)

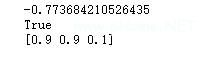
print(res.fun)

print(res.success)

print(res.x)

结果：

作者：心凉丶丶以上就是关于对python中线性规划中的单纯形法、scipy库与非线性规划求解问题的详细介绍。欢迎大家对python中线性规划中的单纯形法、scipy库与非线性规划求解问题内容提出宝贵意见