本文探讨股票价格遵循对数正态分布的特性，解释了μ、x和σ的含义，并通过数学推导分析了lnST与ST的关系，以及E(lnST)与lnE(ST)之间的定量和定性联系。证明过程中涉及伊藤引理和连续复利计算的收益率期望值。参考了约翰·赫尔的相关著作。
关于股票价格的对数正态分布，有几个重要性质，曲曲菜在本文中总结一下，并说明得出过程。
几个参数的说明
μ：股票每年的期望收益率。是投资者在很短一段时间内获得收益率的期望值(按年计)，股票的漂移率除以期初股价。在非常小的时间区间上才有意义，是短时值的年化。本值与利率水平和股票的非系统性风险有关。本质是一个期望值。
x：在长为T的一段时间内，以连续复利计算的股票的收益率。x=(ln(ST/S0))/T。
σ ：股票价格每年的波动率。可以定义为连续复利股票在一年内所提供收益率的标准差。也可以定义为很短一段时间内获得收益率标准差的年化。
1. dST = μSTdt+σSdz = μSTdt+σSdz =
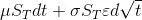
这个式子是我们根据变化规律，为股票价格建模的式子。
2. lnST-lnS0~
最低0.47元/天 解锁文章
扫一扫
1008
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
