非期望产出的sbm模型_期望和条件期望

本文主要讨论期望和条件期望的性质。我们将说明：在L2损失下，数学期望E(Y)是Y的最优常数拟合，而条件数学期望E(Y|X)则是Y的最优函数拟合。即我们有

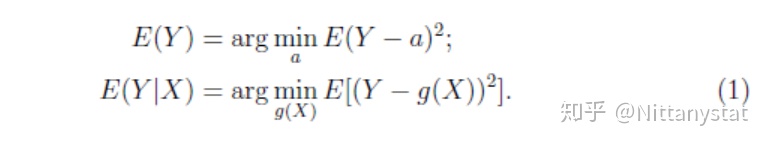
1. 意义
通常，Y被称为响应变量，是我们需要进行拟合或者控制的变量，而X称为自变量。上述结果表明，在没有自变量的时候，Y的最优拟合值即为数学期望E(Y)。而如果存在自变量X，最优拟合则变为E(Y|X)。当然，上述讨论均在L2损失下。如果损失函数发生变化，对应的最优拟合也将发生改变。比如若考虑L1损失，则相应的最优解变为中位数和条件中位数。

在回归分析中，有这样一个常识，即自变量个数越多，往往拟合效果越好。这一现象可以从上式进行解释。现在考虑自变量X,Z，那么根据上式我们得到：

实际上，E(Y|X,Z)和E(Y|X)均为(X,Z)的函数，而在所有(X,Z)的函数中，E(Y|X,Z)对应的L2损失最小。这说明，在回归拟合中，应尽可能地收集和响应变量Y相关的自变量，以使得拟合误差尽可能的小。

那么是不是自变量越多越好呢？答案依赖于我们怎么定义“好”？如果从拟合的角度，的确自变量越多越好。但变量的增加会使得模型的复杂度增加，自变量之间的共线性变强，使得最终的估计结果变差。另外自变量增加后会降低拟合结果的解释性。因此我们需要在模型拟合和模型复杂度之间做一个平衡。这样的思考自然地引出了模型选择方法AIC（Akaike information criterion）和BIC（Bayesian Information Criterion）。也是现今各种惩罚估计量如LASSO和SCAD等方法的基本思路。

上述结果还解释了为何回归分析在统计学当中起到了非常核心的作用。根据上述结果，在L2损失下，E(Y|X)是Y的最优函数拟合。那么如何利用数据拟合条件数学期望呢？这依赖于我们对数据的认识。如果认为自变量和响应变量之间是线性关系，那么我们可以建立线性回归模型。如果对于自变量和响应变量之间的关系并不明确，则可以利用k最近邻方法来局部地近似E(Y|X)。如The Elements of Statistical Learning书中所指，如今绝大多数最受欢迎的技巧都是这两种基本思想的变形。实际上，这两种建模思路也类似参数统计和非参数统计的思想。当对数据存在一定认识时，我们应利用上这种认识以此来提高估计的精度和解释性。但先验的结构认识可能是错的，为避免这种情况，采用更灵活的建模方式是适当的。但相应地，会损失估计精度和解释性。